Overview of tasks for interviewing algorithms - generating sets

Hi, Habr!

This post begins the analysis of the problems of the algorithms that large IT companies (Mail.Ru Group, Google, etc.) so like to give candidates for interviews (if it is bad to pass an interview on algorithms, then the chances of getting a job in a dream company, alas , tend to zero). First of all, this post is useful for those who have no experience in Olympiad programming or heavyweight courses like ShADA or LKSH, in which the subject of algorithms is taken seriously enough, or for those who want to refresh their knowledge in a particular area.

In this case, it cannot be argued that all the tasks that will be dealt with here will necessarily meet at the interview, however, the approaches with the help of which such tasks are solved are, in most cases, similar.

The narration will be divided into different topics, and we will begin by generating sets with a certain structure.

1. Let's start with the bayan-bayanych: you need to generate all the correct bracket sequences with brackets of the same type ( what is the correct bracket sequence ), where the number of brackets is equal to k.

This problem can be solved in several ways. Let's start with recursive .

In this method, it is assumed that we begin to iterate through sequences from an empty list. After the bracket is added to the list (opening or closing), the recursion is called again and the conditions are checked. What are the conditions? It is necessary to monitor the difference between opening and closing brackets ( cnt variable) - you cannot add a closing bracket to the list if this difference is not positive, otherwise the bracket sequence will no longer be correct. It remains to accurately implement this in the code.

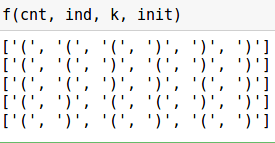
 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

The complexity of this algorithm is $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$extra memory is required $$$O (k)$.

With the given parameters, the function call $$$f (cnt, ind, k, init)$will output the following:

An iterative way to solve this problem: in this case the idea will be fundamentally different - you need to introduce the concept of lexicographic order for bracket sequences.

All correct bracket sequences for one type of brackets can be ordered taking into account the fact that $$$'(' <')'$. For example, for n = 6, the most lexicographically younger sequence would be $$$((()))$and the oldest $$$() () ()$.

To get the next lexicographic sequence, you need to find the rightmost opening bracket, which is preceded by a closing one, so that when they are swapped in places, the bracket sequence remains correct. We will swap them and make the suffix the most lexicographic junior - for this you need to calculate the difference between the number of brackets at each step.

In my opinion, this approach is a little dreary than recursive, but it can be used to solve other problems for generating sets. Implement it in code.

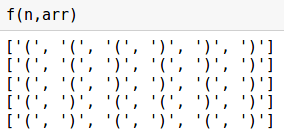
 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

The complexity of this algorithm is the same as in the previous example.

By the way, there is an uncomplicated method that demonstrates that the number of generated bracket sequences for a given n / 2 must match the Catalan numbers .

Works!

Great, with brackets, for now, let's move on to generating subsets. Let's start with a simple puzzle.

2. Given an ascending array of numbers from $$$0$before $$$n-1$, it is required to generate all its subsets.

Note that the number of subsets of such a set is exactly $$$2 ^ n$. If each subset is represented as an array of indices, where $$$0$means that the element is not in the set, but $$$1$- what is included, then the generation of all such arrays will be the generation of all subsets.

If we consider the bitwise representation of numbers from 0 to $$$2 ^ n - 1$, they will define the desired subsets. That is, to solve the problem it is necessary to realize the addition of one to a binary number. We start with all zeros and end with an array in which there is one.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

The complexity of this algorithm is $$$O (n * 2 ^ n)$, by memory - $$$O (n)$.

Now slightly complicate the previous task.

3. Given an ordered array in ascending order with numbers from $$$0$before $$$n-1$need to generate all of it $$$k$-element subsets (solve iteratively).

I note that in terms of the formulation, this task is similar to the previous one and it can be solved using approximately the same methodology: take the initial array with $$$k$units and $$$n-k$zeros and iterate over all variants of such sequences of length $$$n.$

However, minor changes are required. We need to go through all $$$k$-digit sets of numbers from $$$0$before $$$n-1$. It is necessary to understand exactly how to sort through the subsets. In this case, you can introduce the concept of lexicographic order for such sets.

Also arrange the sequence by character codes: $$$1 <0$(This, of course, is strange, but it is necessary, and now we will understand why). For example, for $$$n = 4, k = 2$the youngest and highest order will be $$$[1,1,0,0]$and $$$[0,0,1,1]$.

It remains to understand how to describe the transition from one sequence to another. Everything is simple: if we change $$$1$on $$$0$, then on the left we write lexicographically minimal, taking into account the preservation of the condition on $$$k$. Code:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

Work example:

The complexity of this algorithm is $$$O (C_n ^ k * n)$, by memory - $$$O (n)$.

4. It is given an ordered array of numbers from $$$0$before $$$n-1$need to generate all of it $$$k$-element subsets (solved recursively).

Now let's try recursion. The idea is simple: this time we will do without a description, see the code.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

Work example:

The complexity is the same as the previous method.

5. Given an ascending array of numbers from $$$0$before $$$n-1$, you want to generate all of its permutations.

We will solve with the help of recursion. The solution is similar to the previous one, where we have an auxiliary list. Initially it is zero if on $$$i$the first place of the element is one, then $$$i$already have a permutation. No sooner said than done:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

Work example:

The complexity of this algorithm is $$$O (n ^ 2 * n!)$, by memory - $$$O (n).$

Now we will consider two very interesting problems for Gray codes . In a nutshell, this is a set of sequences of the same length, where each sequence differs from its neighbors in one bit.

6. Generate all two-dimensional Gray codes of length n.

The idea of ​​solving this problem is cool, but if you don’t know the solution, it can be very difficult to guess. I note that the number of such sequences is $$$2 ^ n$.

We will solve iteratively. Suppose we have generated some part of such sequences and they lie in some list. If we duplicate such a list and write it in reverse order, then the last sequence in the first list matches the first sequence in the second list, the penultimate one matches the second, and so on. Let's combine these lists into one.

What needs to be done so that all the sequences in the list differ from each other in one bit? Put in the appropriate places one unit in the elements of the second list to get Gray codes.

It is difficult to perceive "by ear", let's depict the iterations of this algorithm.

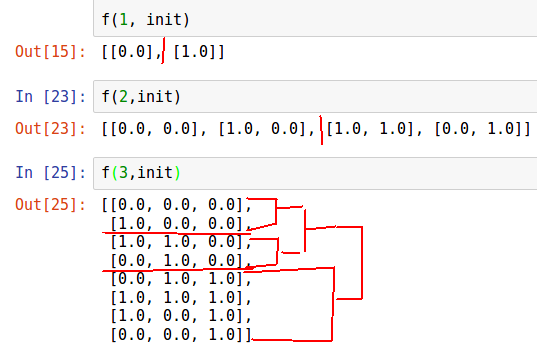
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

The difficulty of this task is $$$O (n * 2 ^ n)$, from memory is the same.

Now let's complicate the task.

7. Generate all Gray k-dimensional codes of length n.

It is clear that the past task is only a special case of this task. However, the beautiful way in which the previous problem was solved, this will not work, here you need to sort out the sequence in the correct order. Let's get a two-dimensional array $$$k * n$. Initially, the last line is one, and the rest are zeros. In this case, the matrix can also occur $$$-1$. Here $$$1$and $$$-1$differ in direction: $$$1$points up $$$-1$points down. Important: in each column at any moment there can be only one $$$1$or $$$-1$, and the remaining numbers will be zeros.

Now we will understand exactly how these sequences can be iterated in order to get Gray codes. We start from the end to move the element up.

In the next step, we rest on the ceiling. Write the resulting sequence. After reaching the limit you need to start working with the next column. Search for it is needed from right to left, and if we find a column that can be moved, then for all columns with which we could not work, the arrows will change in the opposite direction so that they can be moved again.

Now you can move the first column down. Move it until it hits the floor. And so on, until all the arrows do not abut the floor or ceiling and there will be no columns that can be moved.

However, in the framework of saving memory, we will solve this problem with the help of two one-dimensional arrays of length $$$n$: in one array will lie the elements of the sequence, and in another their direction (arrows).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

Work example:

The complexity of the algorithm - $$$O (n * k ^ n)$, by memory - $$$O (n)$.

The correctness of this algorithm is proved by induction on $$$n$, here I will not describe the evidence.

In the next post we will analyze the problem on the dynamics.