Building orbits of celestial bodies by means of Python

Reference Systems for Determining Orbits

To find the trajectories of relative motions in classical mechanics, we use the assumption of absolute time in all reference systems (both inertial and non-inertial).

Using this assumption, we consider the motion of the same point in two different reference systems. $$$K$ and $$$K ^ {'}$ of which the second moves relative to the first with an arbitrary speed $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ where $$$\ vec {R (t)}$ radius vector describing the position of the origin point of the coordinate system $$$K ^ {'}$ relative to the reference system $$$K$ ).
')
We will describe the motion of a point in the system. $$$K ^ {'}$ radius vector $$$\ vec {r ^ {'}} (t)$ directed from the origin of the system $$$K ^ {'}$ at the current position of the point. Then the motion of the considered point relative to the reference system $$$K$ described by radius vector $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ , (one)

and relative speed $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ , (2)

Where $$$\ dot {\ vec {r ^ {'}}} (t)$ - point speed relative to the system $$$K ^ {'}$ ; $$$\ dot {\ vec {R}} (t)$ - speed of movement of the reference system $$$K ^ {'}$ relative to the reference system $$$K$ .



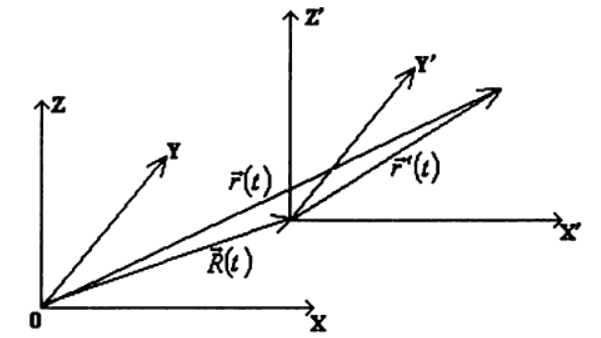
Thus, to find the law of motion of a point in an arbitrary frame of reference $$$K$ it is necessary:

1) set the law of motion of a point - $$$\ vec {r ^ {'}} (t)$ relative to the reference system $$$K ^ {'}$ ;
2) set the law of motion - $$$\ vec {R} (t)$ reference systems $$$K ^ {'}$ relative to the reference system $$$K$
3) to determine the law of motion of a point - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ relative to the reference system $$$K$ .

Construction of the Moon's orbit in the heliocentric reference system

In the heliocentric reference system (system $$$K$ ) The earth moves in a circle of radius
$$$R_ {1} = 1,496 \ cdot 10 ^ {8}$ km (period of circulation $$$T_ {1} = 3.156 \ cdot 10 ^ {7}$ with.). The moon, in turn, moves around the Earth (system K ') around a circle of radius $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km (circulation period $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ with. As is known [1,2], when a material point moves along a circle of radius $$$R$ with constant angular velocity $$$\ omega$ The coordinates of the radius vector drawn from the origin to the current position of the point vary according to the law:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})}, (3)$$

Where $$$\ varphi _ {0}$ - the initial phase characterizing the position of the particle at the moment of time $$$t = 0$ which we will assume to be zero later on. Replacing in (3) $$$R$ on $$$R_ {1}$ and $$$R_ {2}$ and substituting in (1), we obtain the dependence of the radius vector of the Moon in the heliocentric coordinate system on time:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)}, (4)$$

Expression (4) sets the moon's orbit ( $$$y = y (x (t))$ ) in parametric form, where the parameter is time. To build the desired orbit by means of Python, we define the radii of the orbits and the periods of rotation of the Earth and the Moon.

The earth moves in the heliocentric coordinate system ( $$$K$ ) its orbit radius and orbital period are respectively equal $$$R_ {1} = 1,496 \ cdot 10 ^ {8} km, T_ {1} = 3,156 \ cdot 10 ^ {7} s$ . The moon moves around the earth in the coordinate system ( $$$K ^ {'}$ ) its orbit radius and orbital period are respectively equal $$$R_ {2} = 3.844 \ cdot 10 ^ {5} km, T_ {2} = 2.36 \ cdot 10 ^ {6} s$ .

Taking into account (4), we define the functions of dependence of coordinates on time:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t), y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

Using (5), we obtain a pair of coordinates for the moon's orbit:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

Let us set the number of points where coordinates N = 1000 and discrete time are calculated on the interval of the period of rotation of the Earth $$$dt = \ frac {T_ {1}} {N}$ . We write a program and build a graph for a positive coordinate change area:


We get:


Pic1

The created schedule allows you to expand the learning task and see what the moon's orbit will be if the radius of the moon's orbit is equal to $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ . . To the reader, even without special knowledge of astronomy, it is clear that the Moon cannot have such an orbit in the non-field of the Earth, but a hypothetical radius is used to study the conditions of the occurrence of loops . Make the appropriate changes to the program:


We get:


Pic2

Comparing the orbits of the moon presented in Fig. 1 and 2, we find their significant differences. To explain the reason for these differences, it is necessary to compare the linear velocities of the Moon in the first and second cases and the linear velocity of the Earth.

Since the direction of the linear velocity of the Earth relative to the Sun, as well as the direction of the linear velocity of the Moon relative to the Earth, changes over time, and the speed remains constant in magnitude.

As a quantitative characteristic of the ratio of the linear velocities of the Moon and Earth in the heliocentric coordinate system, choose the difference between the module of the linear velocity of the Earth and the projection of the linear velocity of the Moon on the direction of the vector of the linear velocity of the Earth:

$$

$$v_ {o} (t) = \ left | \ vec {V} (t) \ right | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |}, (7)$$

Define the functions that describe the laws of changes in the components of the velocity of the Earth and the Moon:

$$

$$\ begin {matrix} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {matrix}, (8)$$

To determine the resulting speed, taking into account the projection, we use the relation:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

We write the program taking into account (5), (8), (9) and the radius of the orbit of the moon $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km:


We get:


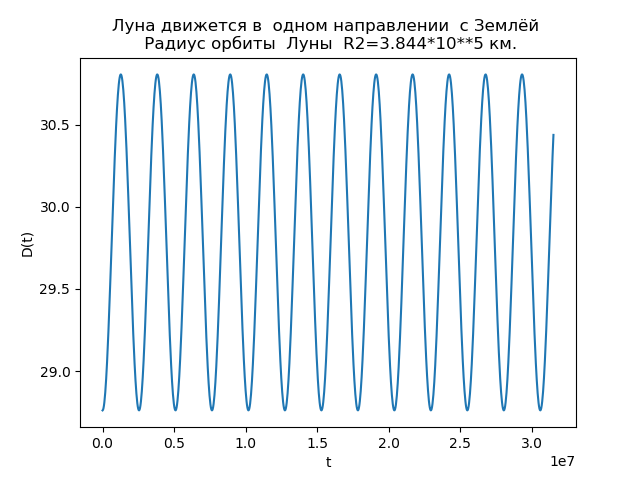
Fig.3.

Let's write the program taking into account (5), (8), (9) and the radius of the Moon's orbit R2 = 3.844 * 10 ** 7 km:


We get:


Fig.4.

Dependency analysis allows us to explain the reason for differences in orbits. D (t) function with $$$R_ {2} = 3,844 \ cdot 10 ^ {5}$ km is always positive, i.e. the moon always moves in the direction of the Earth’s motion and no loops form. With $$$R_ {2} = 3,844 \ cdot 10 ^ {7}$ km magnitude $$$D (t)$ takes negative values, and there are times in which the moon moves in the opposite direction of the Earth’s motion, and therefore the orbit has loops. That was the meaning of using the non-existent orbit of the Moon in the calculations.

The construction of the orbit of Mars in the reference system associated with the Earth

.


In the heliocentric reference system (system K), the Earth moves around a circle of radius $$$R_ {1} = 1,496 \ cdot 10 ^ {8}$ km, period of circulation $$$T_ {1} = $ 365.2$ day, Mars moves along an ellipse, the semi-major axis of which $$$am = 2.28 \ cdot 10 ^ {8}$ km, the period of revolution of Mars $$$T_ {m} = $ 689.9$ day., eccentricity of the orbit $$$e = 0,093$ [3]. The motion of the Earth is described by the radius vector R (t) given by expression (3). Due to the fact that the orbit of Mars is an ellipse, the dependencies $$$x = x (t), y = y (t)$ from time are set parametrically [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ , (ten)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ , (eleven)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ , (12)

A complete ellipse turn corresponds to a change in the parameter <img $$$\ varepsilon$ from 0 to $$$2 \ pi$ . To build the orbit of Mars, at the same time, it is necessary to calculate the coordinates of the radius vectors describing the position of the Earth and Mars in the heliocentric frame of reference, then in accordance with the relation $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ calculate the coordinates of Mars in the reference system associated with the Earth.

To build the orbit of Mars in the reference system associated with the Earth, we use the previously given parameters of the orbits of the Earth and Mars, relations (10) - (12), as well as relations for the coordinates of the Earth:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ , (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ ,(14)

It should be noted that the number of periods of rotation of Mars around the Sun is equal to $$$K = 9$ , then the number of points at which the calculation should be made and the distance between them will be determined from the relations:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


We get:


Pic.5

Calculate the coordinates of the radius vector describing the position of Mars in the reference system associated with the Earth, and build orbits (Fig. 6) using the relation:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i} ))$ (sixteen)


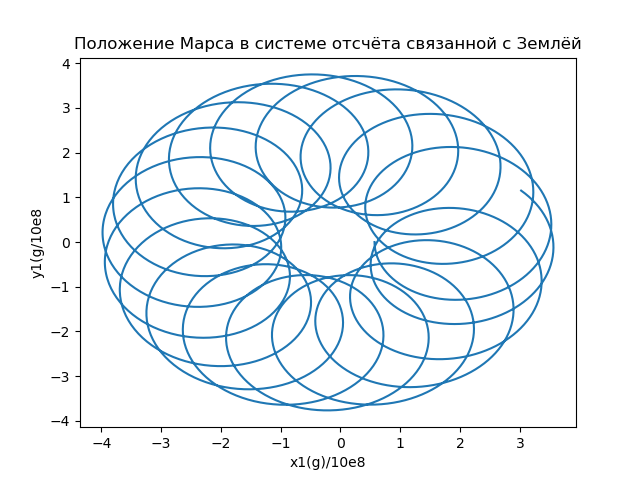
Pic.6

Another important characteristic of the motion of Mars (primarily for interplanetary space flights) is the distance between the Earth and Mars s (t), which is determined by the module of the radius vector describing the position of Mars in the reference system associated with the Earth. The dependence of the distance between the Earth and Mars on time, measured in Earth years, is shown in Fig.7.


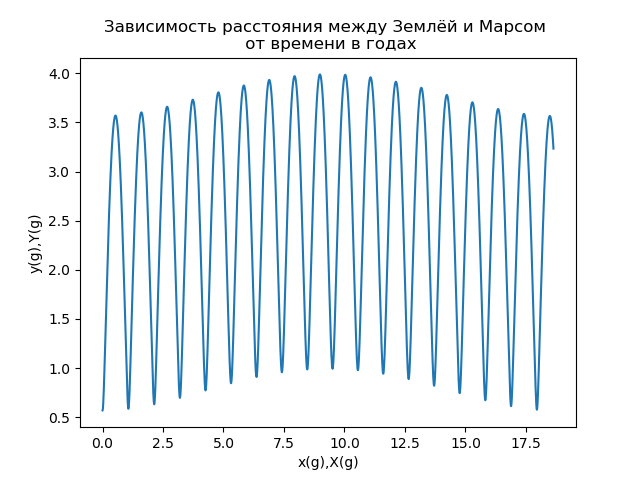
Fig.7

The analysis of the dependence presented in Fig. 7 shows that the distance between the Earth and Mars is a complex periodic function of time. If we use the terminology of the theory of signals [5], then the dependence s (t) can be said that it is an amplitude-modulated signal, which is usually represented as a product of two functions of the high-frequency (carrier) and low-frequency function, which specifies the amplitude modulation (envelope) :

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

Where $$$\ bar {u}$ - constant component of the function $$$u (t)$ ; $$$a$ - signal amplitude; $$$\ omega_ {1}$ - carrier frequency; $$$\ Delta a$ - the amplitude of the function that specifies the depth of amplitude modulation; $$$\ omega_ {2}$ - frequency of the modulating function.

It is seen from Fig. 7 that the carrier period is approximately 2 years, the period of the modulating function is approximately 17 years] 6].

Creation of the heliocentric orbit of Halley's comet

The last time Halley's comet passed through its perihelion (the point of the orbit closest to the Sun) was on February 9, 1986. (The Sun itself is considered to be located at the origin.)

The coordinates and velocity components of Halley’s comet at that moment were equal $$$p_ {0} = (0.325514, 0.459460, 0.166229)$ and $$$v_ {0} = (–9.096111, –6.916686, –1.305721)$ accordingly, the distance here is expressed in astronomical units of length - AU, or simply AU (an astronomical unit, i.e., the length of the major major semiaxis of the earth's orbit), and time — in years. In these units, the three-dimensional equations of motion of the comet are:

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right., (18)$$

(18)

Where: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


We get:









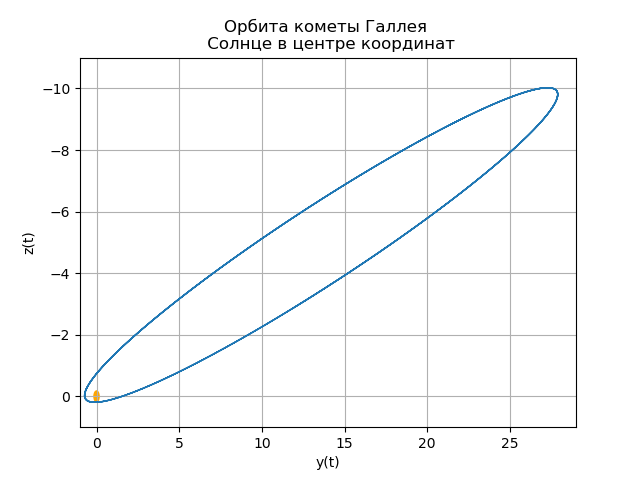
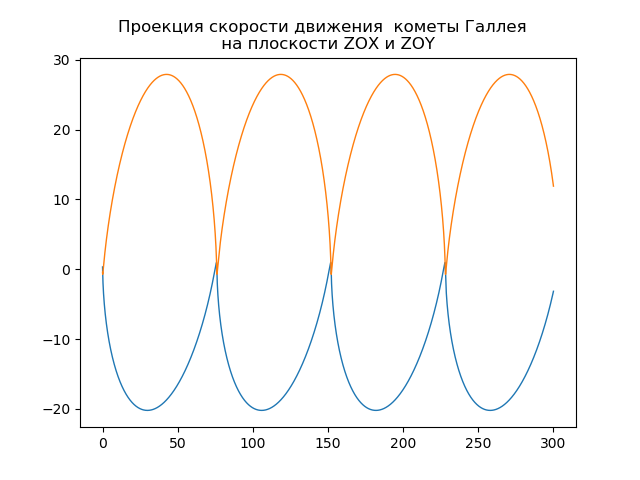
Your own comet

Try an experiment. At night, you set up your telescope on a peak, not far from your home’s elevation. The night should be clear, cloudless, stellar, and if fortune smiled at you: at 0.30 am you will notice a new comet.

After repeated observations on the following nights, you will be able to calculate its coordinates on that first night. Coordinates in the heliocentric coordinate system: P0 = (x0, y0, z0) and the velocity vector v0 = (vx0, vy0, vz0).

Using this data, determine:

• distance of the comet from the Sun at perihelion (the point of the orbit closest to the Sun) and aphelion (the point of the orbit farthest from the Sun);
• the speed of the comet during its passage through perihelion and through aphelion;
• the period of circulation of the comet around the sun;
• The following two dates of passage of the comet through perihelion.

If you measure the distance in astronomical units, and time - in years, then the equation of motion of the comet will take the form (18). For your own comet, choose arbitrary starting coordinates and velocities of the same order as that of comet Halley.

If necessary, re-perform an arbitrary choice of the initial position and velocity vector until you get a plausible eccentric orbit that goes beyond the limits of the Earth's orbit (like most true comets).

References:

1. Feynman R., Leighton R., Sands M. The Feynman Lectures on Physics. 3rd ed. T. 1.-2. M .: Mir, 1977.
2. Matveev A. N. Mechanics and Theory of Relativity. M .: Higher. shk., 1986.
3. Physical Encyclopedia. T. 3. M .: Great Russian Encyclopedia, 1992.
4. Landau L. D., Lifshits E. M. The course of theoretical physics. Mechanics. M .: Fyut-Matgiz, 1958.
5. Baskakov S.I. Radio engineering circuits and signals. M .: Higher. shk., 1988.
6. Porshnev C.V. Computer simulation of physical processes using the mathcad package.