Some tasks of school mathematics
Based on the article "On one task that is no longer offered at the interview."
To begin, consider the task that still can offer at the interview.
38. Calculate the amount ("Tasks for children from 5 to 15 years")
')
(with an error of not more than 1% of the answer)
The algorithm for calculating the partial sums of this series in the Scheme (Lisp) language in the drRacket environment (drRacket allows you to perform calculations in ordinary fractions):
The last two examples drRacket calculated with an error

If we consider partial sums in ordinary fractions, we can see that the sum of the series is equal to
I recall that at
The second volume of the Course of Differential and Integral Calculus 363 (4) deals with the general case
This program can be run at the online ide ide.com and codepad.org .
Consider another example of the problem book.
43. The numbers of rabbits ("Fibonacci"), form a sequence wherein for all . Find the greatest common divisor of numbers and .
Answer: The two adjacent Fibonacci numbers are mutually simple, i.e.
(gcd is the greatest common divisor, i.e., gcd).
Proof from the book “Behind the pages of the textbook of mathematics” [10-11]:
Proof that The book is not given, but according to the Euclidean algorithm
Where - remainder of the division on
and since for the Fibonacci numbers
that
Another example from the problem book
53. For a sequence of Fibonacci numbers task 43 find the relationship limit aspiring to infinity:
The answer is: the "golden section" .
Consider the segments representing the difference between two adjacent members of the series .

Even number members represent growing sequence
Odd row members represent descending sequence
By the nested intervals lemma (Course of differential and integral calculus, 38)
For our series at the point fair equality
Dividing on get equation .
Replacing , we get a quadratic equation .
If in the program geogebra connect the arcs of a circle point 2 and , and , and etc. - we get a self-similar figure

The following example from the problem book
54. Calculate infinite continued fraction.
UPD . Consider the equation
According to Theorems 236 and 235 from the book "Theory of Numbers":
Compiling a table of values and at
so that
and since that
Consider the problem from the book "Behind the pages of the textbook of mathematics" [10-11]
4. Show the number equal to the number that sets the golden ratio.
Consider the option
Course of differential and integral calculus, 35 (2)
From which we can conclude that the "golden section" is a solution to the equation
at .
Next, I would like to consider the algorithm for calculating the inverse of the number given in the textbook
Course in Differential and Integral Calculus, 35 (3)
Algorithm for calculating the inverse of the number in Python:
( Ideone.com and codepad.org )
The reciprocal function accepts a number as input. initial value , number of iterations and returns an array of "approximations" to the number .
at
at
at
etc.
Examples of the reciprocal function for various
[0.1, 0.17, 0.2533, 0.31411733000000003, 0.3322255689810133, 0.3333296519077525,
0.3333333332926746, 0.33333333333333337, 0.33333333333333337, 0.33333333333333337]
[0.1, 0.12, 0.1248, 0.12499968, 0.1249999999991808, 0.125, 0.125, 0.125, 0.125, 0.125]
[0.1, 0.150000000000002, 0.18750000000000003, 0.19921875000000003, 0.19999694824218753, 0.19999999995343333, 0.2000000000000000, 0.19999999999999998,
0.19999999999999998, 0.19999999999999998]
Let's try to use the tangent method to approximate the inverse number.
Tangents to the function graph expressed by the formula
Substituting numbers instead get the tangent equations
Build these graphics
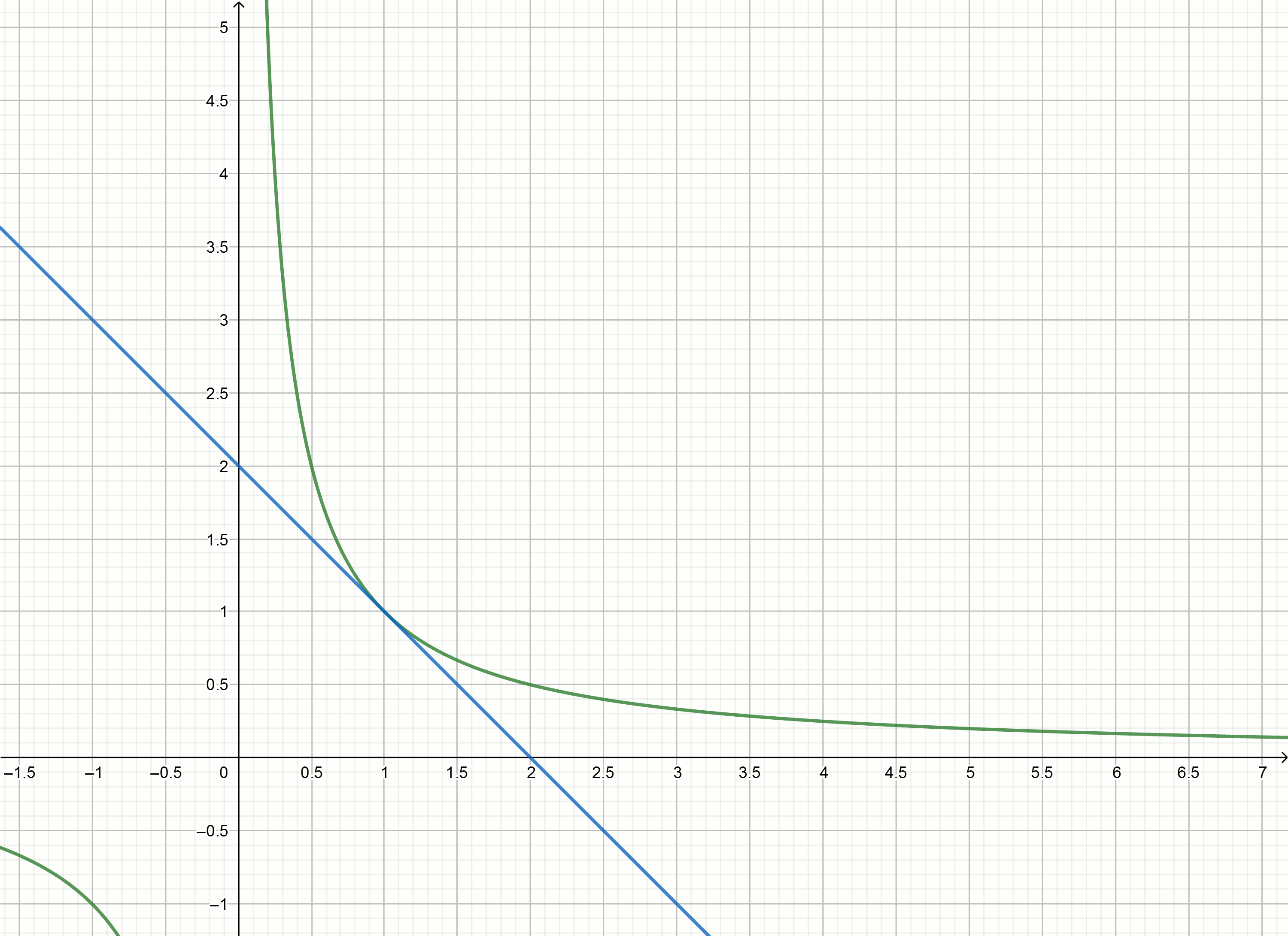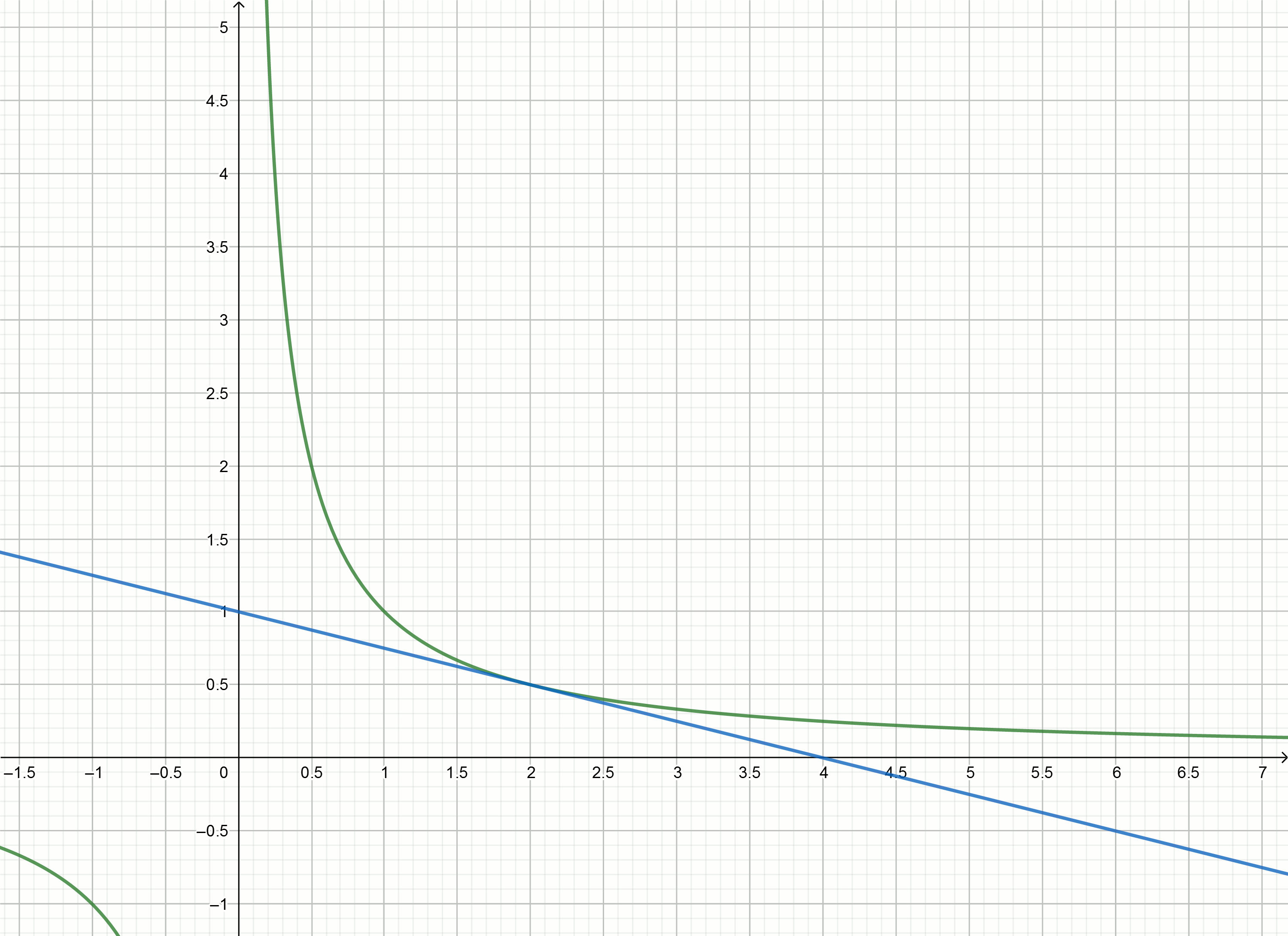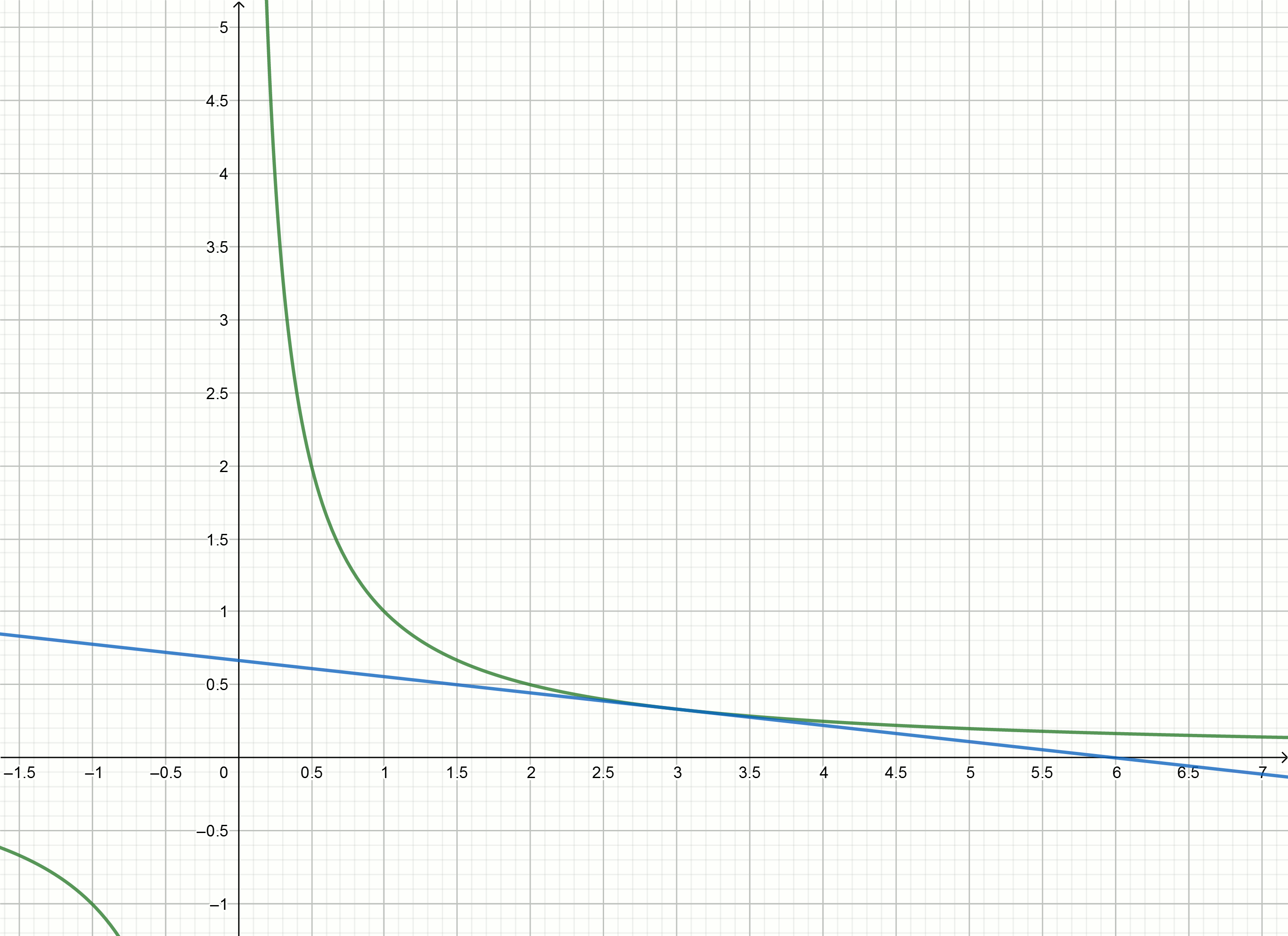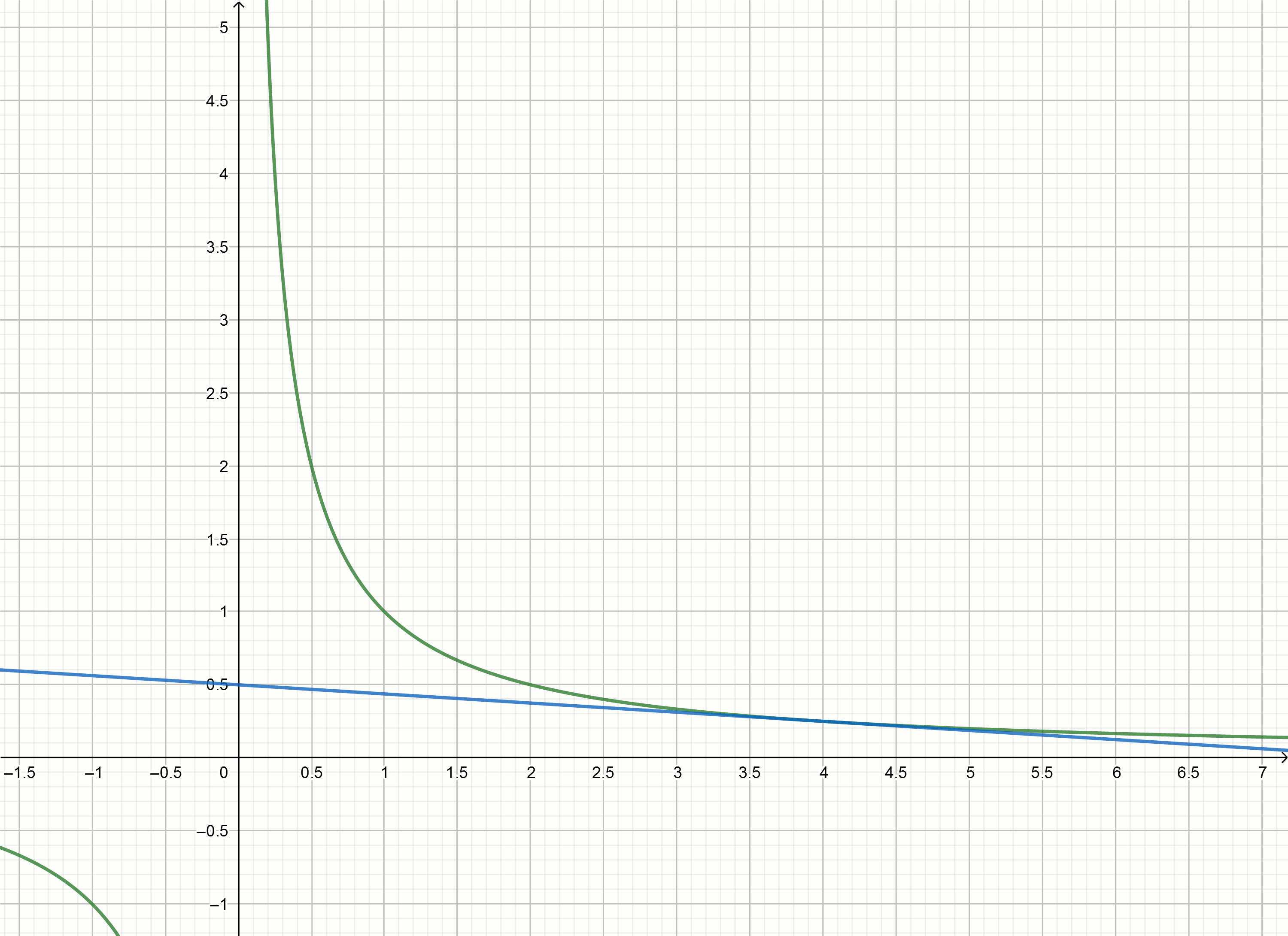
If you move the hyperbole down on then it crosses the x-axis at .
The tangent equation is converted to
Next, equating the tangent equation to zero and expressing get equation
Instead substitute
Instead substitute
Get the expression
Opening the brackets, we get
Substitute into the equation and see what values will "run through" at get
Substituting these values into the equation get straight
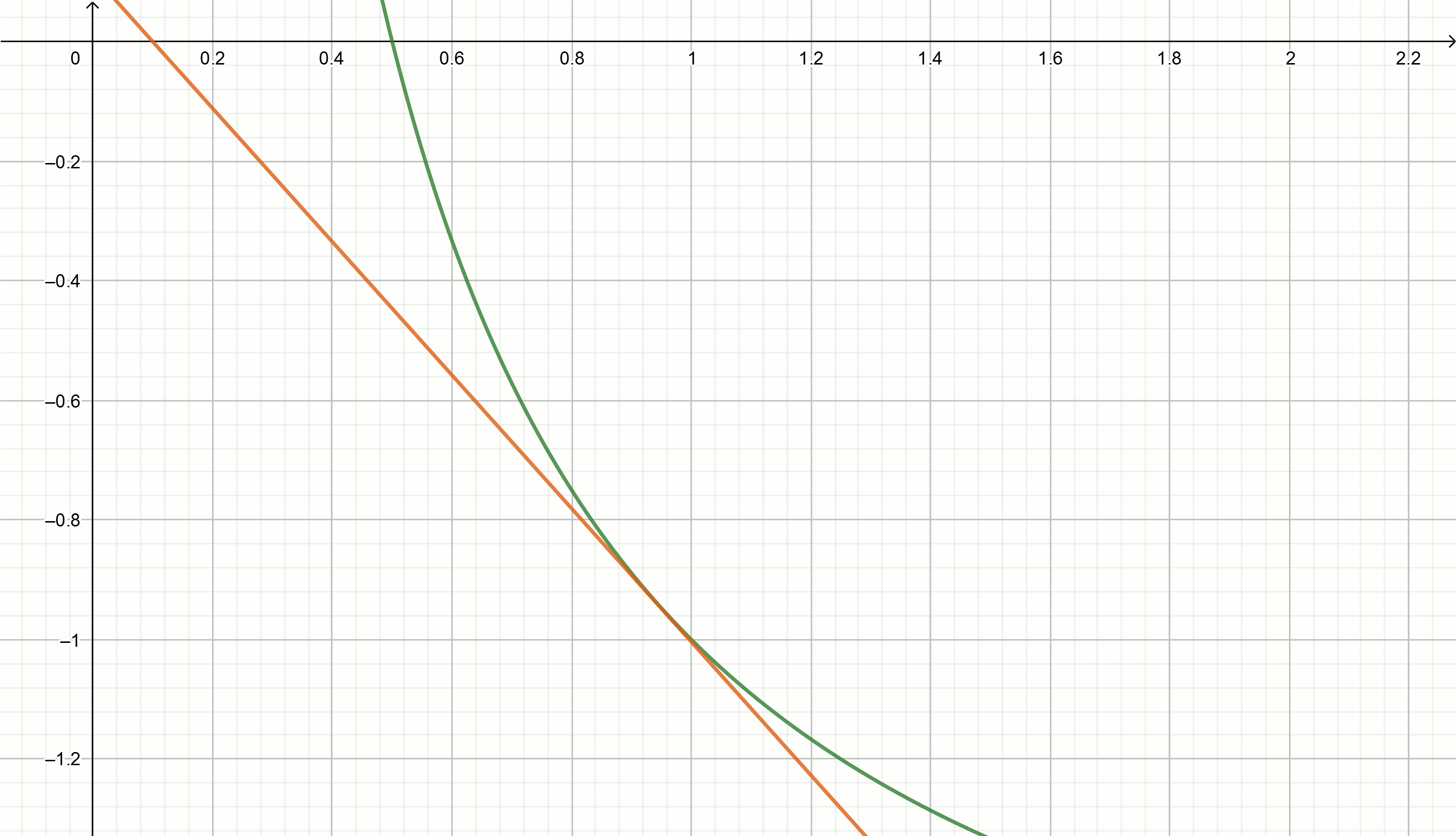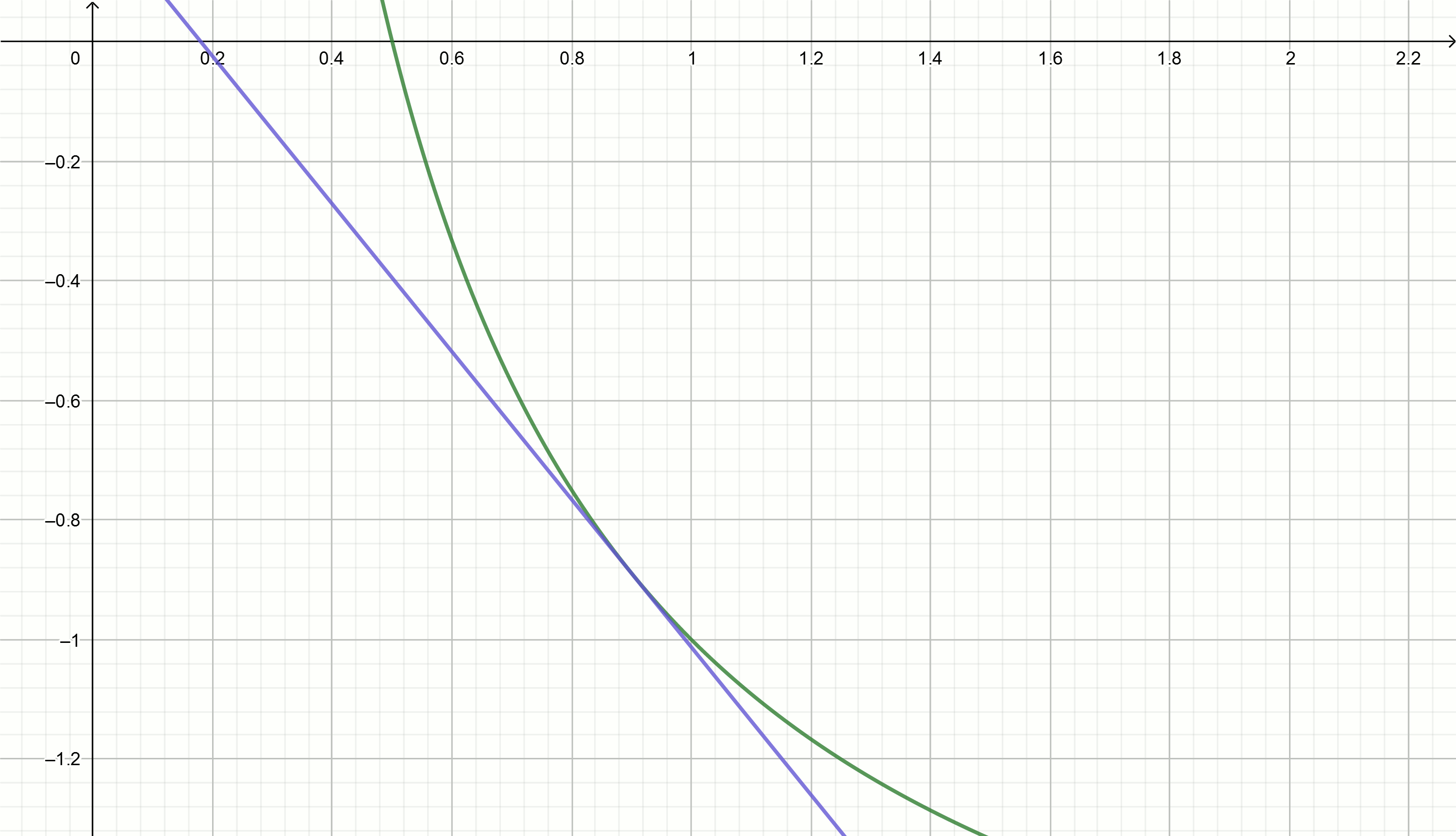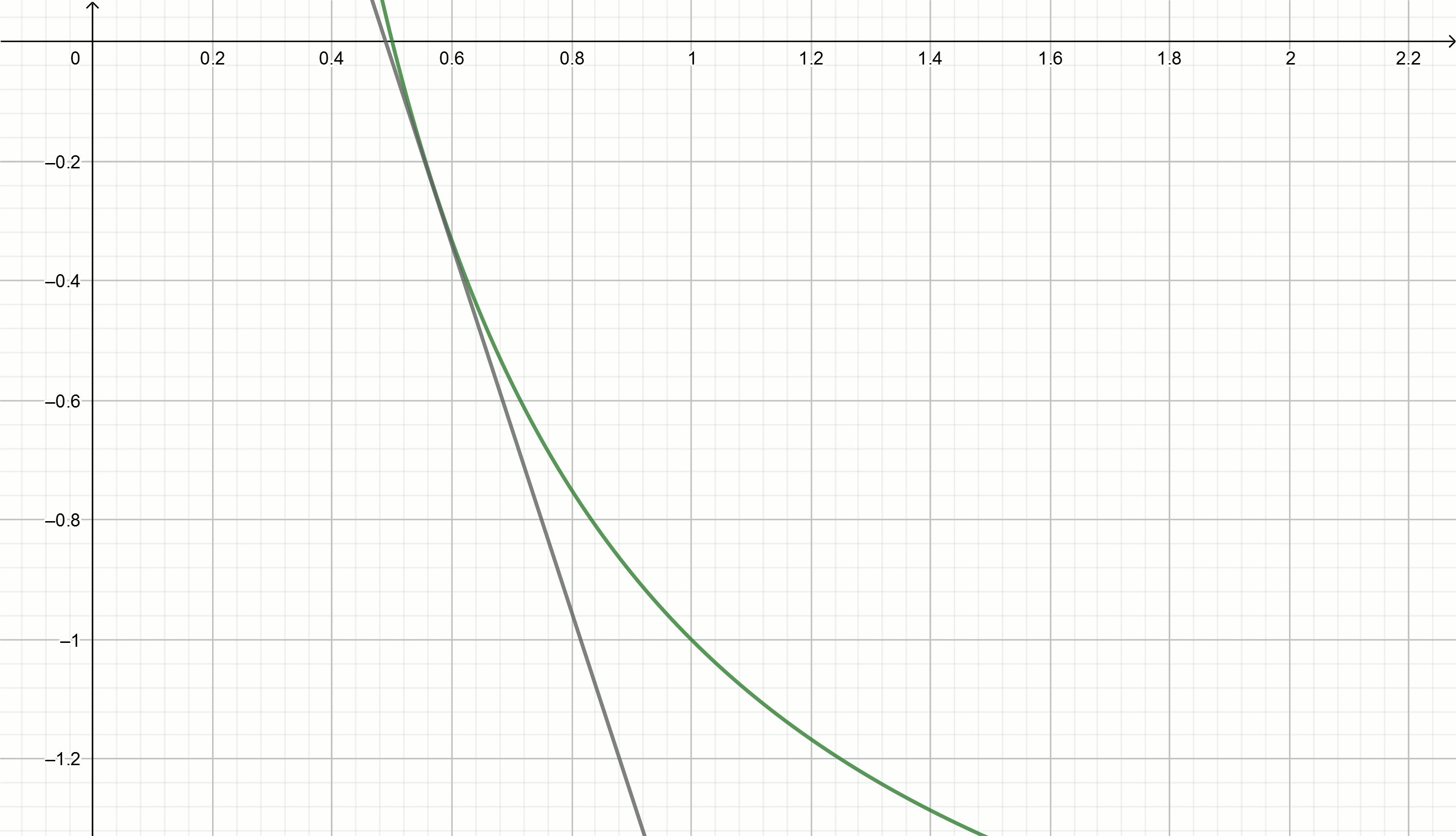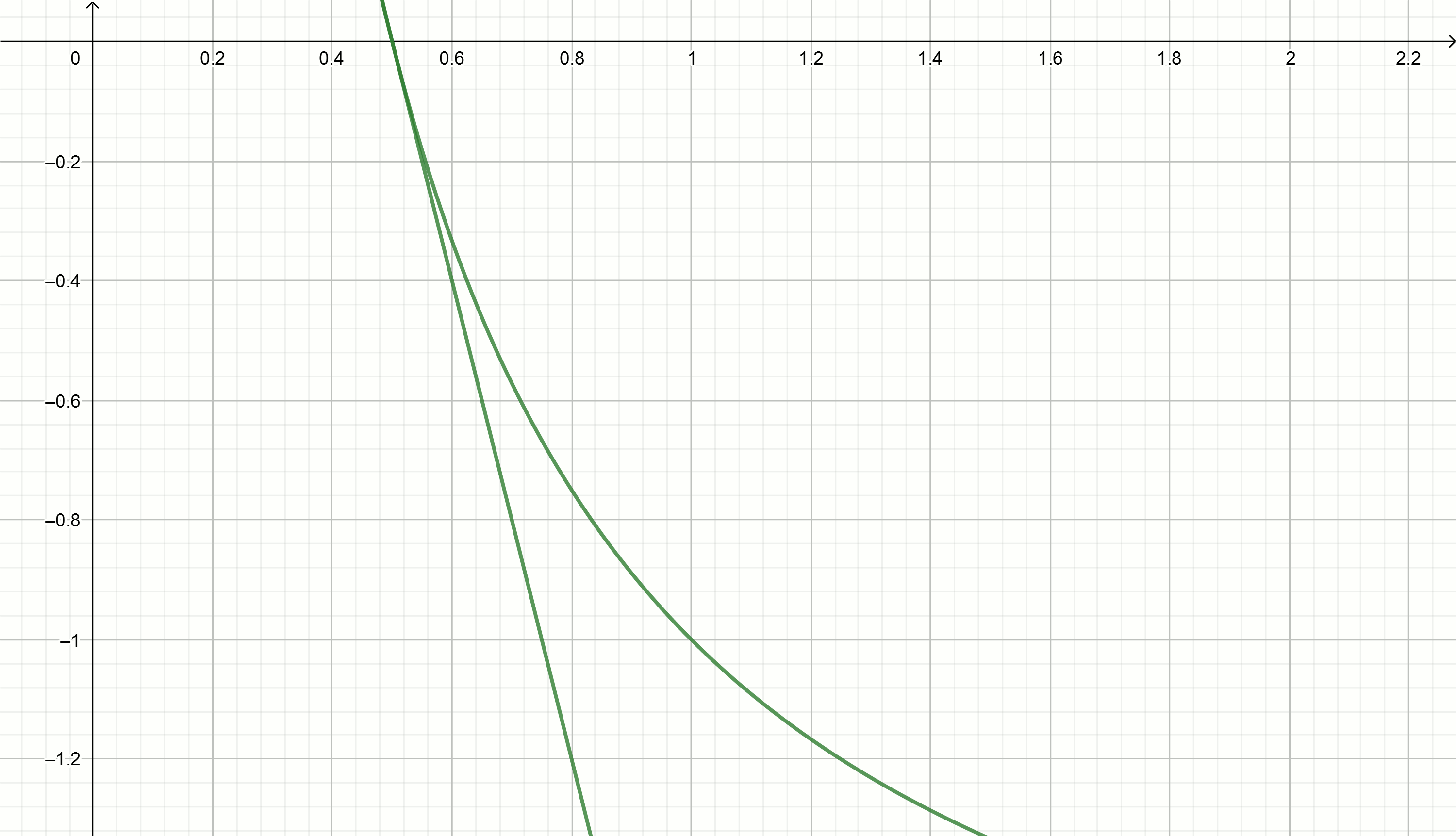
Returning to the irrational expressions, consider the iterative method of extracting the square root.
Write an algorithm using the iterative Heron method
codepad.org
Calculating the square root using continued fractions used by Raphael Bombelli
So we can write the square root algorithm using a continued fraction decomposition
codepad.org
In general, real numerators and denominators can be real and complex numbers, as well as functions of one or several variables.
The method of extracting the integer part allows us to represent an irrational number in the form of an infinite continued fraction with units in the numerators (with frequent numerators equal to one).
Here is an example of a continued fractional number expansion. from the book "Algebra"
If a , the continued fraction purely periodic.
This hypothesis was proved by Evariste Galois .
Those. if to the non-periodic fraction add the whole part then you get a purely periodic fraction .
If in the decomposition of the root according to the method of Bombelli
add to the first term , we get a purely periodic fraction
It remains to bring the fraction to a more familiar form (with units in the numerator).
Divide the numerator and denominator of the fraction by get expression
In this way
Write a program that calculates the approximation of a continued fraction.
codepad.org
In the fourth step we get which is equal to , while .
PS Solve the problem ("Tasks for children from 5 to 15 years")
27. Prove that the remainder of dividing the number on a simple odd number
equals
(examples: .
This task is discussed in the article The Amazing Adventures of the Kvant Magazine fractions .
Books:
“Tasks for children from 5 to 15 years old”, V.I. Arnold.
"The course of differential and integral calculus", G.M. Fichtengolts.
"Theory of Numbers", A. A. Buchstav.
“Behind the pages of a mathematics textbook”, N. Ya. Vilenkin, L. P. Shibasov, Z. F. Shibasova.
"Digital Arithmetic" Ercegovac Milos D., Lang Tomas.
To begin, consider the task that still can offer at the interview.
38. Calculate the amount ("Tasks for children from 5 to 15 years")
')
(with an error of not more than 1% of the answer)
The algorithm for calculating the partial sums of this series in the Scheme (Lisp) language in the drRacket environment (drRacket allows you to perform calculations in ordinary fractions):
#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) The last two examples drRacket calculated with an error

If we consider partial sums in ordinary fractions, we can see that the sum of the series is equal to
I recall that at
The second volume of the Course of Differential and Integral Calculus 363 (4) deals with the general case
This program can be run at the online ide ide.com and codepad.org .
Let us turn to the main topic of the article.
Consider another example of the problem book.
43. The numbers of rabbits ("Fibonacci"), form a sequence wherein for all . Find the greatest common divisor of numbers and .
Answer: The two adjacent Fibonacci numbers are mutually simple, i.e.
(gcd is the greatest common divisor, i.e., gcd).
Proof from the book “Behind the pages of the textbook of mathematics” [10-11]:
Out of equality follows that . Backing away in this way, we come to , and therefore two adjacent Fibonacci numbers are mutually simple.
Proof that The book is not given, but according to the Euclidean algorithm
Where - remainder of the division on
and since for the Fibonacci numbers
that
Another example from the problem book
53. For a sequence of Fibonacci numbers task 43 find the relationship limit aspiring to infinity:
The answer is: the "golden section" .
Consider the segments representing the difference between two adjacent members of the series .

Even number members represent growing sequence
Odd row members represent descending sequence
By the nested intervals lemma (Course of differential and integral calculus, 38)
For our series at the point fair equality
Dividing on get equation .
Replacing , we get a quadratic equation .
If in the program geogebra connect the arcs of a circle point 2 and , and , and etc. - we get a self-similar figure

The following example from the problem book
54. Calculate infinite continued fraction.
UPD . Consider the equation
According to Theorems 236 and 235 from the book "Theory of Numbers":
Compiling a table of values and at
| one | 2 | |
|---|---|---|
| P | one | 3 |
| Q | one | 2 |
so that
and since that
Consider the problem from the book "Behind the pages of the textbook of mathematics" [10-11]
4. Show the number equal to the number that sets the golden ratio.
Consider the option
Course of differential and integral calculus, 35 (2)
In this way is obtained from according to the formula
... According to the main theorem, option has a finite limit . To determine it, go to the limit in equality
We will get, in such a way that satisfies the quadratic equation
This equation has roots of different signs; but the limit of interest can not be negative, therefore, is exactly the positive root:
From which we can conclude that the "golden section" is a solution to the equation
at .
Next, I would like to consider the algorithm for calculating the inverse of the number given in the textbook
Consider the option
Course in Differential and Integral Calculus, 35 (3)
Let be - any positive number, and set . The recurrence relation written above will be replaced as follows:
Taking the initial value under the condition: , we get that , monotonously increasing, will strive for . According to this scheme, on the counting machines the number, the inverse, is calculated. .
Algorithm for calculating the inverse of the number in Python:
( Ideone.com and codepad.org )
def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr The reciprocal function accepts a number as input. initial value , number of iterations and returns an array of "approximations" to the number .
at
at
at
etc.
Examples of the reciprocal function for various
>>> reciprocal(3,0.1,10) [0.1, 0.17, 0.2533, 0.31411733000000003, 0.3322255689810133, 0.3333296519077525,
0.3333333332926746, 0.33333333333333337, 0.33333333333333337, 0.33333333333333337]
>>> reciprocal(8,0.1,10) [0.1, 0.12, 0.1248, 0.12499968, 0.1249999999991808, 0.125, 0.125, 0.125, 0.125, 0.125]
>>> reciprocal(5,0.1,10) [0.1, 0.150000000000002, 0.18750000000000003, 0.19921875000000003, 0.19999694824218753, 0.19999999995343333, 0.2000000000000000, 0.19999999999999998,
0.19999999999999998, 0.19999999999999998]
Geometric interpretation
Let's try to use the tangent method to approximate the inverse number.
Tangents to the function graph expressed by the formula
Substituting numbers instead get the tangent equations
Build these graphics

If you move the hyperbole down on then it crosses the x-axis at .
The tangent equation is converted to
Next, equating the tangent equation to zero and expressing get equation
Instead substitute
Instead substitute
Get the expression
Opening the brackets, we get
Substitute into the equation and see what values will "run through" at get
Substituting these values into the equation get straight

Square root extraction
Returning to the irrational expressions, consider the iterative method of extracting the square root.
Write an algorithm using the iterative Heron method
def square_root(a,n): # a - , n - x0=1 # 1 arr=[] for i in range(n): arr.append(x0) # x0=0.5*(x0+a/x0) # return arr print square_root(2,10) codepad.org
Calculating the square root using continued fractions used by Raphael Bombelli
To find the value , first we define its integer approximation: where . Then . From here it is easy to infer that . Re-substituting the resulting expression in the formula , we get a continued fraction decomposition:
So we can write the square root algorithm using a continued fraction decomposition
def square_root(n,a,n_count): # n- , a - x0=a # a arr=[] for i in range(n_count): # a arr.append(x0-a) # a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) codepad.org
In general, real numerators and denominators can be real and complex numbers, as well as functions of one or several variables.
The method of extracting the integer part allows us to represent an irrational number in the form of an infinite continued fraction with units in the numerators (with frequent numerators equal to one).
Here is an example of a continued fractional number expansion. from the book "Algebra"
In this way,
Select the integer part of the number . So can be represented as . It's clear that , so . Again, eliminate the irrationality in the numerator of the second term:
The result was:
Let's do one more similar step:
It is easy to see that the process of isolating the whole part and forming a continued fraction in this example has no end. Each new denominator will appear and addend . Therefore, it is clear that is represented as an infinite continued fraction:
Hypothesis
If a , the continued fraction purely periodic.
This hypothesis was proved by Evariste Galois .
Those. if to the non-periodic fraction add the whole part then you get a purely periodic fraction .
If in the decomposition of the root according to the method of Bombelli
add to the first term , we get a purely periodic fraction
It remains to bring the fraction to a more familiar form (with units in the numerator).
Divide the numerator and denominator of the fraction by get expression
In this way
Write a program that calculates the approximation of a continued fraction.
#lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) codepad.org
In the fourth step we get which is equal to , while .
PS Solve the problem ("Tasks for children from 5 to 15 years")
27. Prove that the remainder of dividing the number on a simple odd number
equals
(examples: .
This task is discussed in the article The Amazing Adventures of the Kvant Magazine fractions .
Books:
“Tasks for children from 5 to 15 years old”, V.I. Arnold.
"The course of differential and integral calculus", G.M. Fichtengolts.
"Theory of Numbers", A. A. Buchstav.
“Behind the pages of a mathematics textbook”, N. Ya. Vilenkin, L. P. Shibasov, Z. F. Shibasova.
"Digital Arithmetic" Ercegovac Milos D., Lang Tomas.
Source: https://habr.com/ru/post/419237/
All Articles