Simulation of water surface using FFT and NeuroMatrix DSP-processor
The already well-known fast Fourier transform is used not only for solving problems of digital signal processing, recognition of objects in an image, but also in computer graphics. Jerry Tessendorf described a mathematical model that allows you to synthesize ocean waves and animate them in real time. The basis of this model is a two-dimensional FFT.
When I was given the task to develop an application for a DSP processor that visualizes the operation of the FFT, I realized that wave modeling is perfect for this purpose.

The basic idea of a mathematical model of a wave can be described by the following expression:
= FFT2D ( ), FFT2D we denote as the operator of the two-dimensional FFT.
- is the height field of the water surface (matrix size where and may take powers of two). The elements of this matrix are wave heights.
')
- signal (matrix size ), generated according to a specific law and time-dependent.
where elements of the matrix this $ inline $ e ^ {iω_ {ij} t} = cos (ω_ {ij} t) + isin (ω_ {ij} t) $ inline $ and matrix - complex conjugate to matrix,
- these are elements of the matrix .
- elementwise multiplication of matrices.
- height field at the initial time t = 0.
- complex conjugate to matrix (by size ).
To create an animation of the movement of waves in real time it is necessary to recalculate the matrix and changing t . Matrices , and calculated once and reused.
We now turn to the description of the DSP processor, which, based on the above formulas, need to be able to:
18796 on the NeuroMatrix architecture, developed in the company NTC Module, was used as a DSP processor. The diagram in Figure 1.
The processor contains 2 parallel cores NMPU0 and NMPU1 (operating at 500 MHz), each of which has a RISC processor and a vector coprocessor (NMCore FPU for floating point and NMCore INT for integer arithmetic). The NMPU0 core is designed to handle floating point data, and the NMPU1 core is integer data. NMPU0 has 8 banks of internal SRAM memory (128 kB each), and NMPU1 has 4 banks (128 kB each) of the same memory. The 1879VM6Y has a DMA controller and a DDR2 interface.
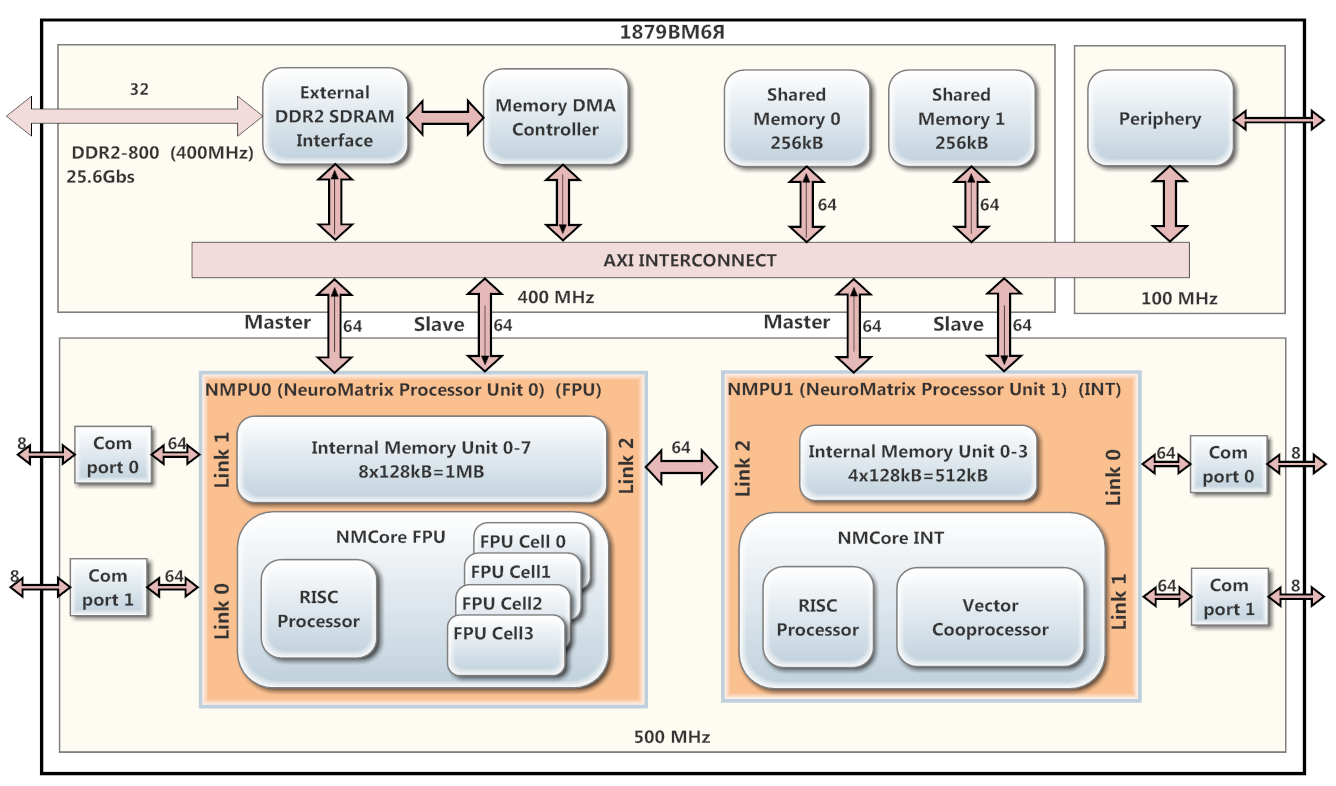
Fig. 1. The scheme of the processor 18796
The processor is located on the tool module MC121.01 (see Fig. 2). Also on this module there is 512 MB of DDR2 memory.

Fig.2. MC121.01
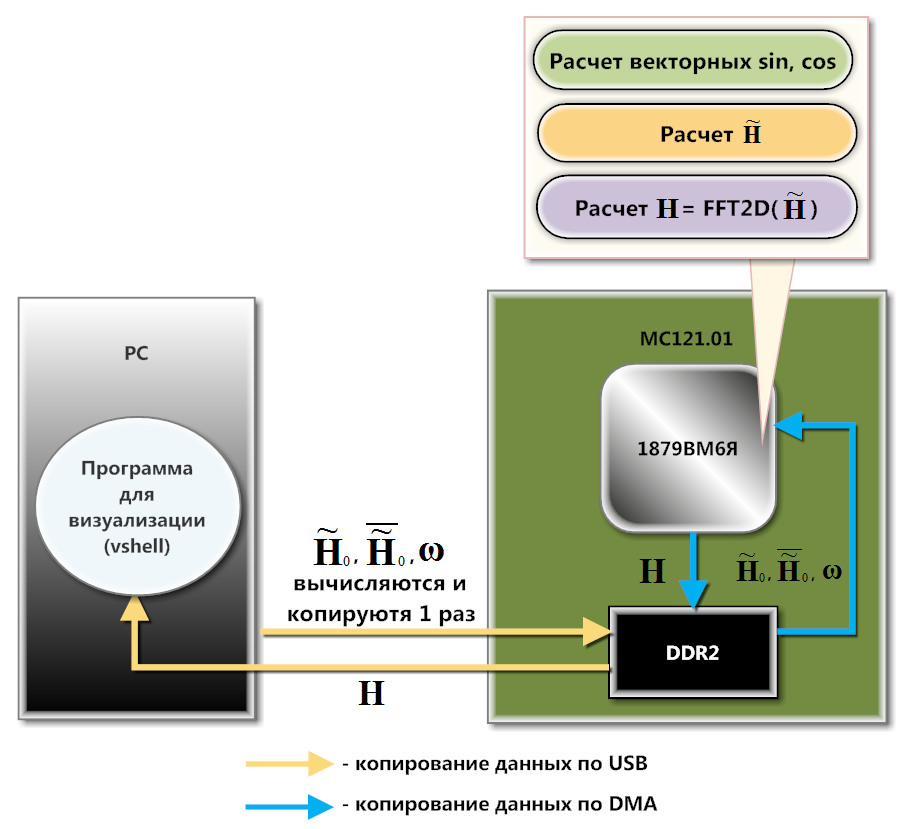
Fig. 3. Scheme of interaction between MC121.01 and PC
The MC121.01 communicates with the PC via USB (the diagram in Figure 3). At the program level, this interaction is organized using the download and data exchange library, which is included in the SDK of this board. Pre-calculated matrices , and loaded into DDR2 memory through the functions of the library download and share. DMA controller copies , and line by line in the internal memory (SRAM) of the processor. Downloading to DDR2 is due to the fact that none of these matrices fit completely into SRAM. Line by line copying takes place here, because 1879BM6I makes calculations from SRAM faster than from DDR2. Moreover, a significant part of the calculations can be done on the background of the work of DMA.
Using the vector functions of the NMPP library to calculate the sines, cosines, multiplication and addition of vectors, the processor calculates the rows of the matrix and takes from them a one-dimensional FFT. The result is sent over DMA back to DDR2. So, an intermediate matrix is formed in DDR2, from the columns of which the processor calculates a one-dimensional FFT (preloading the columns of the intermediate matrix by DMA into SRAM). Thus, a matrix is formed in DDR2. . This matrix is downloaded to the PC to draw a single frame with the image of a wave surface. To animate a picture in real time, you need to calculate the matrix using the algorithm described above. by increasing the parameter t .
In practice, it turns out that 18796 calculates the matrix faster than the PC pumps it out. Because of this, the processor may be idle, waiting for the PC to take the next piece of data. This problem was solved with the help of a ring buffer (containing several matrices). ), organized in DDR2 memory board.
At the software level, work with the DMA controller and the ring buffer is performed using the HAL (Hardware abstraction Level) library functions for NeuroMatrix processors.
When the height field matrix loaded into PC memory, you can visualize the surface. To display it more clearly, you need x, y, z coordinates, describing the surface points, multiplied by the rotation matrix . So we get the new coordinates of the surface x ', y', z ', turning it at a certain angle.
Scaling new coordinates and connecting points along them with straight lines, you can see the animation of ocean waves (see the video below). To visualize the surface, a library for displaying images on the vshell screen was used.
In conclusion, I would like to say that the calculation and transfer of one matrix via USB 256x256 float numbers spent ~ 4.7 million cycles (72 clocks per float). The frame rate is ~ 107. If you do not take into account the time spent on data transmission via USB, the calculations will cost ~ 2.5 million cycles (38 cycles per float). This is the total time spent by the 18796 processor on elementwise multiplications and addition of matrices, calculations of FFT, sines, cosines and copying using DMA. These calculations are performed against the background of data transfer via USB.
The difference of 2.2 mln. Cycles (4.7 mln. - 2.5 mln. = 2.2 mln.) Indicates that in the PC system - MS121.01 USB is a bottleneck, and 1879VM6Ya can be loaded with calculations by 46% more, without getting FPS drawdown.
I would also like to note that, against the background of data transfer via USB and computations on a floating point coprocessor, a coprocessor can be used for integer arithmetic, which was not used in this problem.
The table shows the performance of some vector functions of the nmpp library.
NMPP - library of primitives for the NeuroMatrix architecture
HAL - a library of abstraction of the hardware-dependent part of NeuroMatrix
VSHELL - library of processing and displaying images
When I was given the task to develop an application for a DSP processor that visualizes the operation of the FFT, I realized that wave modeling is perfect for this purpose.

Mathematical wave model
The basic idea of a mathematical model of a wave can be described by the following expression:
= FFT2D ( ), FFT2D we denote as the operator of the two-dimensional FFT.
- is the height field of the water surface (matrix size where and may take powers of two). The elements of this matrix are wave heights.
')
- signal (matrix size ), generated according to a specific law and time-dependent.
where elements of the matrix this $ inline $ e ^ {iω_ {ij} t} = cos (ω_ {ij} t) + isin (ω_ {ij} t) $ inline $ and matrix - complex conjugate to matrix,
- these are elements of the matrix .
- elementwise multiplication of matrices.
- height field at the initial time t = 0.
- complex conjugate to matrix (by size ).
To create an animation of the movement of waves in real time it is necessary to recalculate the matrix and changing t . Matrices , and calculated once and reused.
We now turn to the description of the DSP processor, which, based on the above formulas, need to be able to:
- Calculate FFT.
- Elementally multiply matrices.
- Add the matrix.
- Calculate the vector of sines and cosines.
18796 on the NeuroMatrix architecture, developed in the company NTC Module, was used as a DSP processor. The diagram in Figure 1.
The processor contains 2 parallel cores NMPU0 and NMPU1 (operating at 500 MHz), each of which has a RISC processor and a vector coprocessor (NMCore FPU for floating point and NMCore INT for integer arithmetic). The NMPU0 core is designed to handle floating point data, and the NMPU1 core is integer data. NMPU0 has 8 banks of internal SRAM memory (128 kB each), and NMPU1 has 4 banks (128 kB each) of the same memory. The 1879VM6Y has a DMA controller and a DDR2 interface.

Fig. 1. The scheme of the processor 18796
The processor is located on the tool module MC121.01 (see Fig. 2). Also on this module there is 512 MB of DDR2 memory.

Fig.2. MC121.01

Fig. 3. Scheme of interaction between MC121.01 and PC
The MC121.01 communicates with the PC via USB (the diagram in Figure 3). At the program level, this interaction is organized using the download and data exchange library, which is included in the SDK of this board. Pre-calculated matrices , and loaded into DDR2 memory through the functions of the library download and share. DMA controller copies , and line by line in the internal memory (SRAM) of the processor. Downloading to DDR2 is due to the fact that none of these matrices fit completely into SRAM. Line by line copying takes place here, because 1879BM6I makes calculations from SRAM faster than from DDR2. Moreover, a significant part of the calculations can be done on the background of the work of DMA.
Using the vector functions of the NMPP library to calculate the sines, cosines, multiplication and addition of vectors, the processor calculates the rows of the matrix and takes from them a one-dimensional FFT. The result is sent over DMA back to DDR2. So, an intermediate matrix is formed in DDR2, from the columns of which the processor calculates a one-dimensional FFT (preloading the columns of the intermediate matrix by DMA into SRAM). Thus, a matrix is formed in DDR2. . This matrix is downloaded to the PC to draw a single frame with the image of a wave surface. To animate a picture in real time, you need to calculate the matrix using the algorithm described above. by increasing the parameter t .
In practice, it turns out that 18796 calculates the matrix faster than the PC pumps it out. Because of this, the processor may be idle, waiting for the PC to take the next piece of data. This problem was solved with the help of a ring buffer (containing several matrices). ), organized in DDR2 memory board.
At the software level, work with the DMA controller and the ring buffer is performed using the HAL (Hardware abstraction Level) library functions for NeuroMatrix processors.
Wave Surface Visualization
When the height field matrix loaded into PC memory, you can visualize the surface. To display it more clearly, you need x, y, z coordinates, describing the surface points, multiplied by the rotation matrix . So we get the new coordinates of the surface x ', y', z ', turning it at a certain angle.
Scaling new coordinates and connecting points along them with straight lines, you can see the animation of ocean waves (see the video below). To visualize the surface, a library for displaying images on the vshell screen was used.
Conclusion
In conclusion, I would like to say that the calculation and transfer of one matrix via USB 256x256 float numbers spent ~ 4.7 million cycles (72 clocks per float). The frame rate is ~ 107. If you do not take into account the time spent on data transmission via USB, the calculations will cost ~ 2.5 million cycles (38 cycles per float). This is the total time spent by the 18796 processor on elementwise multiplications and addition of matrices, calculations of FFT, sines, cosines and copying using DMA. These calculations are performed against the background of data transfer via USB.
The difference of 2.2 mln. Cycles (4.7 mln. - 2.5 mln. = 2.2 mln.) Indicates that in the PC system - MS121.01 USB is a bottleneck, and 1879VM6Ya can be loaded with calculations by 46% more, without getting FPS drawdown.
I would also like to note that, against the background of data transfer via USB and computations on a floating point coprocessor, a coprocessor can be used for integer arithmetic, which was not used in this problem.
The table shows the performance of some vector functions of the nmpp library.
| Function | So you |
|---|---|
| One-dimensional FFT, 256 points | 1770 |
| Sine, 256 points | 1400 |
| Cosine, 256 points | 1400 |
References:
NMPP - library of primitives for the NeuroMatrix architecture
HAL - a library of abstraction of the hardware-dependent part of NeuroMatrix
VSHELL - library of processing and displaying images
Source: https://habr.com/ru/post/419161/
All Articles