Dynamic programming in olympiad problems
Hello!
Recently I solved problems from the Timus Online Judge archive and came across a section called dynamic programming tasks . Tasks of this type make me particularly interested, because often this approach ensures the speed and elegance of the solution. What is dynamic programming?
Dynamic programming is an approach to problem solving, in which there is a division into subtasks that are “simpler” in comparison with the original one. The word "dynamic" is close in meaning to "inductive": it is assumed that the answer is known for some value and I want to find the answer for . In mathematics, this is called an inductive transition, and constitutes the basic idea of dynamic programming.
')
The most striking and illustrative task is the task of computing th Fibonacci sequence number. It is known that the sequence has the following properties:
This immediately implies the recurrence formula:
If the recursion searches for the number “from the end”, then the following method sequentially calculates all the numbers between and :
It is clear that with sufficiently large This algorithm is much faster: it does not calculate intermediate values several times. Consider a slightly more complex example.
Example 1. You walk up the toll ladder. To step on step you need to pay of coins. You can step to the next step or jump over one. Task: to pass steps and spend as little coins as possible.
It is clear that stepping over each step, we minimize the number of "payments", but we can run into a very expensive step that we would like to avoid. Create an array of values in which on The first place will be the (minimum) number of coins that must be spent to get to th steps. It is immediately clear that . And then we will take at least two previous steps and add the cost of the step itself:
We change the conditions of the problem a little: suppose that at some steps you can receive coins (this will mean that ). What needs to be changed in the algorithm so that it gives the correct result?
Consider another example that uses the "two-dimensional" dynamics.
Example 2. The maze has rooms, each of which is gold (in a cage lies gold). The task is to determine what the maximum amount of gold can be collected with the optimal route from the point exactly if you can go either down or to the right.
So, we want to know the optimal route to the cell. . Here we can get from two cells - and . Given that the optimal routes for these two cells are known (they are stored in a table ), then the answer is for the cell is obtained as follows:
This is another classic dynamic programming problem, modifications of which are quite often encountered in problems of sports programming. More similar problem is explained here .
The mathematical formulation of the problem is as follows: it is required to find the minimum number of terms required to decompose a given number into full squares.
As before, suppose we know the answers for all numbers. that are stored in an array and we would like to find .
Take this number and analyze what could be the situation:
In general, the option of adding one to the previous one does not seem so bad.
We proceed as follows: we will seek expansion such that
Consider the following problem . The goal is to build a ladder from cubes by the rules:
This time we will build a two-dimensional dynamics. Create a tab in which position will lie the number of stairs consisting of cubes whose height does not exceed . If it works, then the answer to our problem will be the amount
So, we will solve the problem of finding the number of stairs composed of cubes that have height . The picture shows the stairs that fall into :
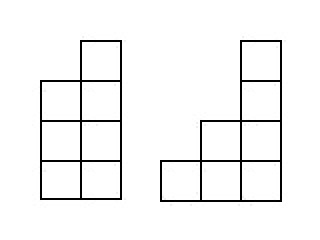
Since we know all the stairs, which consist of a smaller number of cubes, we “split” from the stairs right column. The result is a staircase c cubes. Example for :
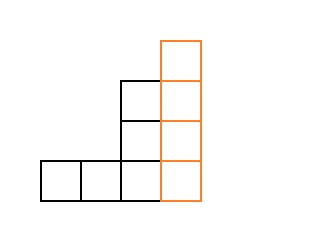
But for such stairs, the result is already known, so we will sort through all such stairs in a cycle and add up all the results. In this way,
Now we will go through the height of the stairs:
Important : in the process of building our matrix, you need to consider , because otherwise, some types of ladders will be “lost” (during “splitting off”), but it goes without saying that such a ladder does not satisfy the conditions of the task, therefore the answer will be the number .
The next problem is solved using a one-dimensional array.
So what we have. The first ent knows 2 words. Each ent teaches all the words that he knows himself, two ents: young and old. In turn, the young were taught as many more words as he already knows, and the old were taught only one word. Need to know how many ents know exactly words (you must print the number of these ents modulo ).
The solution is quite simple. Create an array in which on th place we will store the number of ents (modulo who know of words. It all starts with the first ent who knows two words, so . And then everything is simple:
It remains to understand the calculation of the module. In order not to store huge numbers, we will immediately memorize all the values in the module.
Resources used:
Recently I solved problems from the Timus Online Judge archive and came across a section called dynamic programming tasks . Tasks of this type make me particularly interested, because often this approach ensures the speed and elegance of the solution. What is dynamic programming?
Dynamic programming is an approach to problem solving, in which there is a division into subtasks that are “simpler” in comparison with the original one. The word "dynamic" is close in meaning to "inductive": it is assumed that the answer is known for some value and I want to find the answer for . In mathematics, this is called an inductive transition, and constitutes the basic idea of dynamic programming.
')
Simple examples
The most striking and illustrative task is the task of computing th Fibonacci sequence number. It is known that the sequence has the following properties:
This immediately implies the recurrence formula:
int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } If the recursion searches for the number “from the end”, then the following method sequentially calculates all the numbers between and :
int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; } It is clear that with sufficiently large This algorithm is much faster: it does not calculate intermediate values several times. Consider a slightly more complex example.
Example 1. You walk up the toll ladder. To step on step you need to pay of coins. You can step to the next step or jump over one. Task: to pass steps and spend as little coins as possible.
It is clear that stepping over each step, we minimize the number of "payments", but we can run into a very expensive step that we would like to avoid. Create an array of values in which on The first place will be the (minimum) number of coins that must be spent to get to th steps. It is immediately clear that . And then we will take at least two previous steps and add the cost of the step itself:
We change the conditions of the problem a little: suppose that at some steps you can receive coins (this will mean that ). What needs to be changed in the algorithm so that it gives the correct result?
Decision
It is necessary to change only the "beginning" of our dynamics. If the first ladder does not bring us coins, then it is advisable to jump over it, however, if it is better to step on and collect your coins. So, .
Consider another example that uses the "two-dimensional" dynamics.
Example 2. The maze has rooms, each of which is gold (in a cage lies gold). The task is to determine what the maximum amount of gold can be collected with the optimal route from the point exactly if you can go either down or to the right.
So, we want to know the optimal route to the cell. . Here we can get from two cells - and . Given that the optimal routes for these two cells are known (they are stored in a table ), then the answer is for the cell is obtained as follows:
This is another classic dynamic programming problem, modifications of which are quite often encountered in problems of sports programming. More similar problem is explained here .
More challenging tasks
If desired, the dynamic approach can be screwed anywhere. Consider a task from the Timus Online Judge archive.The mathematical formulation of the problem is as follows: it is required to find the minimum number of terms required to decompose a given number into full squares.
As before, suppose we know the answers for all numbers. that are stored in an array and we would like to find .
Take this number and analyze what could be the situation:
- is a complete square. In this case .
- Perhaps the previous number was a complete square. Then .
In general, the option of adding one to the previous one does not seem so bad.
We proceed as follows: we will seek expansion such that
Because - full square, then and
that is, we found a partition that is simply better than and the answer in this case will be
Sample Java code that implements this algorithm:
for(int k = 1; k <= n; k++) { int best = d[k - 1] + 1; // int q = 1; while(k - q*q >= 0) { // k = q*q + s if(k - q*q == 0) { // k - best = 1; break; } else if(d[k - q*q] < best) best = d[k - q*q] + 1; q++; } d[k] = best; } Consider the following problem . The goal is to build a ladder from cubes by the rules:
- the staircase has at least two steps;
- a staircase cannot have two identical steps;
- steps of a ladder go in ascending order (that is, the next one is greater than the previous one).
This time we will build a two-dimensional dynamics. Create a tab in which position will lie the number of stairs consisting of cubes whose height does not exceed . If it works, then the answer to our problem will be the amount
So, we will solve the problem of finding the number of stairs composed of cubes that have height . The picture shows the stairs that fall into :

Since we know all the stairs, which consist of a smaller number of cubes, we “split” from the stairs right column. The result is a staircase c cubes. Example for :
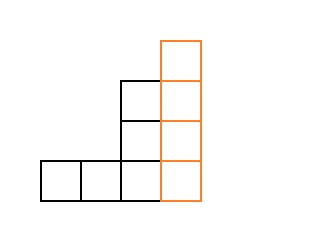
But for such stairs, the result is already known, so we will sort through all such stairs in a cycle and add up all the results. In this way,
Now we will go through the height of the stairs:
Finally, changing from before will get the answer.
Important : in the process of building our matrix, you need to consider , because otherwise, some types of ladders will be “lost” (during “splitting off”), but it goes without saying that such a ladder does not satisfy the conditions of the task, therefore the answer will be the number .
Sample Java code that implements this algorithm:
dp = new long[n + 1][n+1]; d[1][1] = 1; d[2][1] = 0; d[2][2] = 1; for(int i = 3; i < n + 1; i++) { for(int j = 2; j <i; j++) { long cnt = 0; for(int k = 1; k < j; k++) { cnt += d[i - j][k]; } d[i][j] = cnt; } d[i][i] = 1; // } long answer = 0L; for(int i = 0; i <= n; i++) { answer += d[n][i]; } answer--; // The next problem is solved using a one-dimensional array.
So what we have. The first ent knows 2 words. Each ent teaches all the words that he knows himself, two ents: young and old. In turn, the young were taught as many more words as he already knows, and the old were taught only one word. Need to know how many ents know exactly words (you must print the number of these ents modulo ).
The solution is quite simple. Create an array in which on th place we will store the number of ents (modulo who know of words. It all starts with the first ent who knows two words, so . And then everything is simple:
- All ents who know an odd number of words are old and could only learn from previous ones. Therefore for odd
- As for the Ents, who know an even number of words - these are all those who received the same number of words from the elves (young) those who have learned from previous ones (old ones); that is, for even we have .
It remains to understand the calculation of the module. In order not to store huge numbers, we will immediately memorize all the values in the module.
Sample Java code that implements this algorithm:
int[] d = new int[K + 1]; if(K >= 2) d[2] = 1; if(P != 1) { for(int i = 3; i <= K; i++) { if(i % 2 != 0) { d[i] = d[i - 1]; } else { d[i] = ((d[i/2] % P) + d[i - 1] % P) % P; } } } else d[K] = 0; Resources used:
- Timus Online Judge;
- A little bit about dynamic programming;
- Comparison properties modulo.
Source: https://habr.com/ru/post/418867/
All Articles