Procedural level generation

Work on programming, graphics and sounds in some new igrahe finished - there were only levels. Light and pleasant work, but for some reason it goes with great difficulty. Perhaps the effect is general fatigue.

Thinking how to simplify my life, the idea of procedural generation came to mind. Obviously, it will also need to be written, but as stated in one famous work, “it’s better to lose a day, then fly in five minutes.”

Attention! Under the cut a lot of text and "fat" gifs.

Introductory

The levels will still be polished manually, so there are no special requirements for memory, speed of work, or even the quality of the levels obtained.

Initially, I planned that the generator would only distribute rooms and doors, and all further refinement (plot, scenery and enemies) would be carried out in manual mode. But at the moment I think that the generator will be able to much more. However, manual refinement will still remain - it is necessary that players feel that at least a little love has been invested in the levels.

I looked through my knowledge base on game development, and wrote out links to procedural generation articles in a separate document. Most, of course, about the generation of classical labyrinths or the generation of relief (by the way, the results are very impressive), which is not suitable for a 3D shooter. But some were close to what I needed (I marked with an asterisk those that seemed to me the most suitable):

I decided to start with the last two - they are simply realized, and they give good results.

Generator structure

In fact, I did not come to this structure immediately, but in the process of numerous refactorings and rewriting, but I write about it immediately, so that it is clear what is happening:

Generation of the original geometry (your choice - or "BSP", or the layout of the premises).
Cleaning garbage sections (such sections that can not exist in the game).
Building connections
Clearing junk subgraphs (such groups of sections that are interconnected, but not connected to the remaining sections).
Clearing of unnecessary connections (construction of a spanning tree , the link is given to the minimum spanning tree, because there is a picture, but for the generator there is no need in the minimum).
Randomization of compounds - restoration of some remote connections back (for a more "human" type of level), as well as the transformation of some others into passages between sections (which "merges" several sections into one of a more complex form).
Generate secret rooms.
Generation of the "script" (where there will be an initial and final section, and which path will have to be traveled in order to get from the initial to the final one).
Compound optimization.
Creating doors and windows.
Select the action to be performed in this section (press the switch, raise the key or find the secret wall).

There are still about 12 points, but they are not completed yet (when I’m done, I’ll write a separate post about them).

Generation of the original geometry: "BSP"

This translation was taken as a basis. I'm not sure how much what is happening in this algorithm is close to a real BSP, so I write "BSP" in quotes.

The algorithm is quite simple. Initially create a rectangle the size of the whole playing field:

Then divide it randomly into two parts - either horizontally or vertically. Where the separation line will be held, we also choose randomly:

Recursively doing the same for new rectangles:

And again and again, to some limit:

Then in each rectangle we select "room" - a rectangle of the same size as the original or smaller (but not less than 3x3 - in more detail about this will be lower).

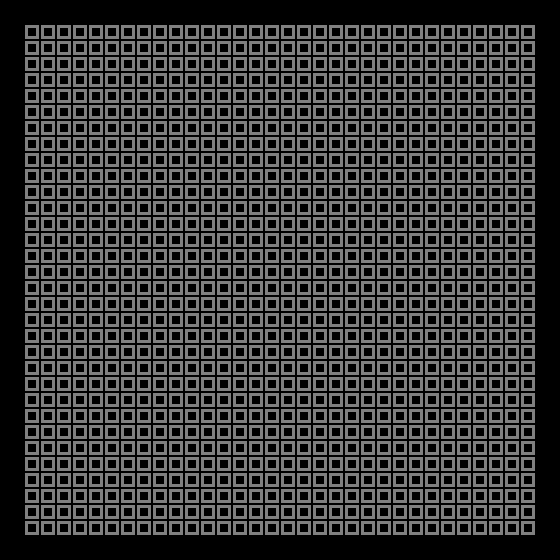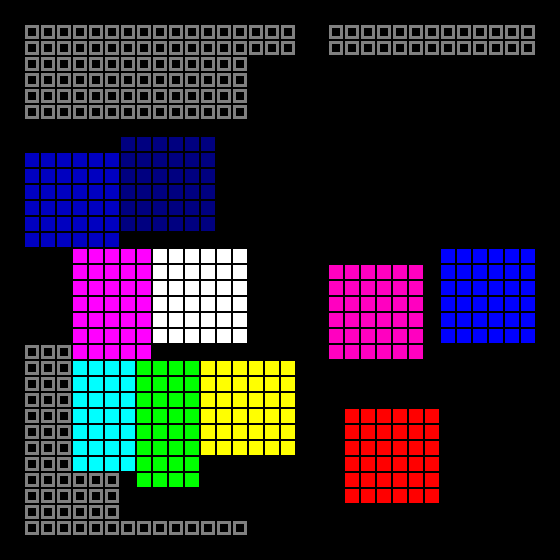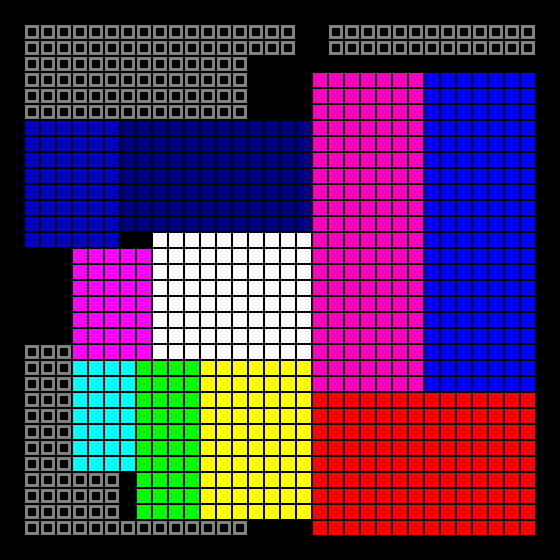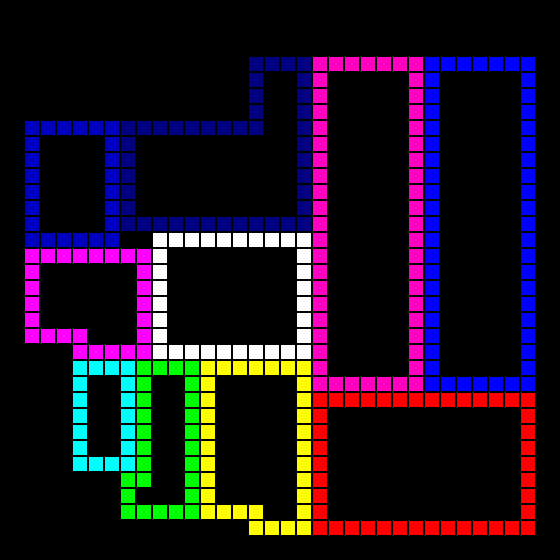
Then the rooms are connected by corridors. But not everyone with each, but somewhat cunning, because of the fact that they are stored in the "BSP" -like structure (for more details, see the original algorithm).

The corridor connecting the purple and white sections.

In the original algorithm, both the rooms and the corridors are of the same color (i.e., equivalent), so there the corridors are simply drawn over the rooms. In my case, the original rooms should be preserved, so that the corridors are drawn as if “behind” the rooms.

In addition, if a room (in the picture is turquoise) crosses the corridor, then it should divide it into two different sections (therefore, the same corridor can be drawn in different colors):

And that's what comes out of it:

Then begins the phase of marking garbage cells:

As I already wrote, no sector can be less than 3x3 cells. This is due to the fact that the sector must be surrounded by walls (at least 1 cell on each side), and there must be at least one free space in it:

Therefore, all those cells that do not fit this rule are marked. But just to take, and you can not remove them - so many connections disappear, and the level is very scanty.

Instead, for each labeled cell, it looks for a sector to which it can join (observing the 3x3 rule):

If a cell cannot be attributed to any sector, it will be deleted (but not in this case, everything is fine here).

At the last stage, this beautiful picture is vectorized, and the drawn sectors turn into polyboxes — such polygons, with each edge either vertically or horizontally (probably, there is a more scientific name):

Generation of the original geometry: room layout

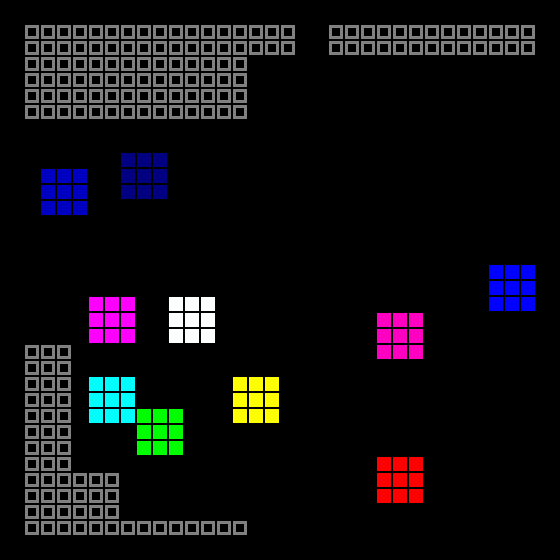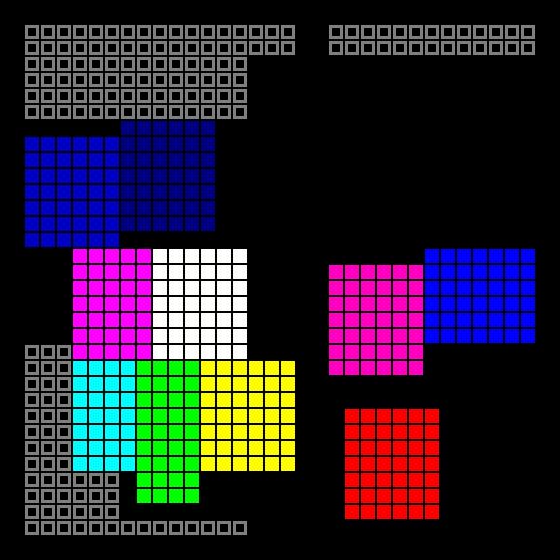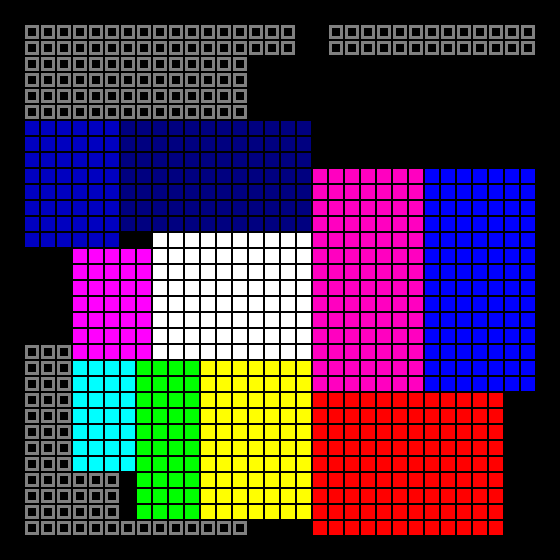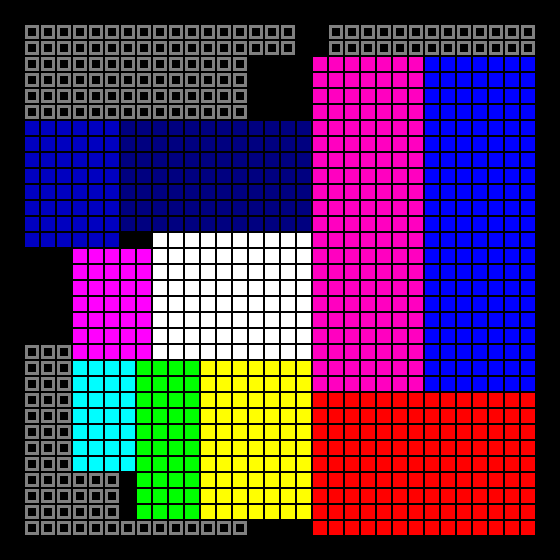
The basis was taken another article . This algorithm is somewhat more complicated than the previous one, but also not rocket science.

To begin with, the playing field is filled with a kind of stop value, and then a rectangular area is cleared randomly on it:

The cleaning stage of a random rectangle is performed some more (also random) times, and as a result, the outer contours of the level are obtained:

In the free space, the growth points of rooms are randomly spread out (the minimum size of a room is 3x3):

The first stage of the growth of rooms begins - for each room, the largest side is selected, which can still grow, and it grows by 1 square (if there are several sides with the same length, random ones). The rooms are moving one by one, so that there are no intersections.

Then the rooms are converted to polyboxes:

And the second stage of growth begins - at this stage the side can be divided into several parts. Unlike the first stage, it does not grow one cell at a time, but immediately to the maximum stop - this allows you to avoid the “ladders” at the joints of the rooms. If after the passage through all the rooms there are still empty cells, the cycle repeats.

The result is a completely filled space:

Next polyboxes are drawn in the form of a raster, and (as in the case of the "BSP" generator) the stage of marking "junk" cells begins:

And joining them to existing sectors:

It was not possible to attach all the cells - the extra ones were deleted.

The result turns back into polyboxes:

Cleaning the garbage sections

Sometimes there are sections within which the 3x3 rule is not respected:

You can try to restore such sections, but I went along a simpler path, and just delete them:

Building connections

For each section, its neighbors are sought, and connections are created at the points of contact of such sections. Connections are created on both sides - if section A is in contact with section B, there will be a connection from A to B and from B to A. The result is a bidirectional graph.

Clearing trash subgraphs

Sometimes, as a result of cleaning the garbage sections, it turns out not one graph, but several independent ones, as in this example:

In this case, the subgraph is chosen as the main one, the “area” of sections is maximum, and the rest are removed (the “area” is in quotes, because although it is possible to calculate the real polybox area, I simplified the task and consider the area of the bounding rectangle - This is wrong, but suitable for the generator).

Purification of unnecessary compounds

If from each sector there is a passage to each with which it is connected, then there will be too many doors at the level, and it will be more felt that it is generated. Therefore, at this stage, extra connections are deleted:

For more randomization, I do not generate a spanning tree in the minimum number of passes, but, on the contrary, I delete one random edge at a time (choosing it randomly from all possible at the current step).

Although, when I was writing this, I had the idea that it would be quite enough to randomly select the starting sector, and deleting the edges would be a more efficient algorithm.

Randomization of compounds

Hereinafter, illustrations will come from another generation, since in the previous one there was an error in the generator, due to which further images were incorrect.

But the level in which there is not a single superfluous connection also does not look very human, therefore some chaos is introduced:

Some deleted edges are restored.
And some turn into passages.

Further, those sections between which the aisles were formed, "merge" into one:

If it seemed to you that the connections removed at the previous step appeared again in this illustration - it seemed to you :). When I was reading the text, it seemed to me that way too, but after looking closely at the previous illustration it becomes clear that everything is ok.

Generate secret rooms

On the graph, select such sectors that have only one connection:

If there are several such sectors, then they are all gathered into an array, and sorted by "area". Then this array is cropped randomly (but so that at least one element remains in it). These sectors will become secret rooms:

Script generation

First, sectors are selected with a minimum number of free connections (ie, those that are closer to the “edge” of the graph):

In this illustration, one sector is selected, but if there were more of them, one would be chosen anyway (randomly).

Nb. While reading the article, I was able to come up with a situation where a sector with a minimum number of free connections would not only be on the edge, but also assigning a scenario to it would lead to an impassable level. In fact, you can choose any sector, but only this one, after removing which the graph would not split into several subgraphs.

Next, select the sectors that are connected to the current sector, and which have only one free connection. With some probability, they will be used to continue the scenario. For example, if the graph were the same as in the illustration below, then the sector indicated by the question could be included in the list.

Gray indicates the secret room, a cross marks those connections that should be removed in the source graph, plus is the source sector.

Nb. During the reading of the article, it seemed to me that the condition of having only one connection was too strict, it would be enough the same as in the last step, so that after the removal of this sector, the graph would not break up.

Next, this list of sectors is assigned a script number (just a number, at this stage it does not mean anything concrete), and connections on the borders of this list of sectors are marked as closed by this script.

In these illustrations, different scenarios will have different colors of the sector fill. They have nothing to do with the color of the edging sector (in the next steps it will fix, but in this step it is more convenient for me).

Then the next sector is selected, a list is compiled, and this list is marked with a new scenario:

Notice the little blue dots inside the red squares - this is how the scenario opener is drawn - i.e. somewhere inside the section with the red script there will be a key or switch that will open the passage to the sectors with the blue script.

This continues until there are no free sectors:

The most recent sector is not assigned a scenario, but only a scenario opener. This sector will be the sector in which the player will start the game.

For this level:

The player starts in the starting sector, somewhere there finds a “opener” to the yellow sector, goes there.
In the yellow sector opens the blue sector, goes there.
In the blue sector opens green, goes there.
In the green sector opens purple, goes there.
In purple opens red.
In red - blue.
Where and finds the end of the level switch.

Schematically, this can be shown as:

Opener can be either a key or a switch, or something else, for example, the task of destroying all enemies in any sector (but I do not plan that in the near future a generator or engine will support this).

Compound Optimization

At this step, one side is selected for each of the connections (as you remember, connections are initially generated in both directions). This is necessary to make the level look more “manual”, and to simplify the next steps (but for an even more interesting level look, in the near future I plan to take a step to “de-optimize” some connections) .

Creating doors and windows

For each sector, all its connections are viewed (which, after the previous step, look only in one direction), and on each viewed connection there are doors and windows.

First, a point is selected at the junction, preferably closer to the center.
Then at this point is placed either a door or a window (and if this is a connection to a secret room, then a secret wall).
If a door is placed, it can be from 1 to 3 cells in size (one is a regular door, two or three is a thick pressure door, which opens after pressing any switch).
Then the connection is divided into two parts - the part before the selected point, and the part after. And, if either before or after a place is left, the function is called recursively.

To make the level look more interesting, at different steps there is a different probability of placing a door or window:

In the first step, the door must be placed, because what's the use of the connection, if there is only one window.
In the second step, a window is placed more likely (75%) than a door.
If there is a third step (for example, a long connection), then a window must be placed on it.
In the case of the 4th step, the door or window is placed equally likely.
If the connection is extra long, the generator returns to the second step.

Choice of action

Although this has nothing to do with generation, the visualization at this step changes - now the edging of the sector is painted in the color of the script:

Starting sector - light gray, the final - blue. Also note that instead of the door at the secret room (dark gray on the left) a wall is drawn - everything is correct, this is a secret wall.

Next, select the sector in which you can place the keys:

They are selected simply enough:

If this is a secret room, then there can be no openers in it, and the key cannot be placed there.
You can not place the key in the final sector - after all, it is the final one.
Also, the key cannot open double and triple doors - due to the nature of the engine, they can only be opened using the switch (in the above illustration there are no such sectors) .

After that, the number of keys at a level (from zero to three) is randomly selected, and then, in the same way, from the available list of sectors, those in which there will be keys are selected.

In other sectors there will be switches.

Source: https://habr.com/ru/post/418685/

All Articles