Building a local map of the robot
Hi, Habr!
In this publication I would like to talk about how I built a local map of patency for the robot. This task was necessary both to improve skills in programming and mastering sensors, and for the subsequent introduction of our own algorithms into the work of real robots at such robotic activities such as Robocross and Robofest.
This article is designed for those who are just entering the world of robotics or trying to figure out how to build a terrain map. I tried to present everything in the simplest and most understandable language that most people can understand.
So, the local cross - country map is what the robot sees at a given time.
This is the information that comes from the “eye” of the robot and is subsequently processed and displayed in a convenient form.
')
If the robot is standing still, then its local map under constant environmental conditions remains constant.
If the robot moves, then at each moment of time its environment is different, respectively, the local map also changes.
A local map usually has a fixed size. The size is calculated based on the maximum length of the beams emitted by the rangefinder. In my case, this length is 6 meters.
To simplify the task, it was decided to make a square map. It was also decided that the range finder would be conventionally located exactly in the center of the map (this place would be the point where x = y = 0). The center was chosen in this way because the range finder that I use emits rays in the plane more than 180 ° (it emits rays at 240 °, but more on that later), that is, some rays will certainly go beyond the scanner and if you choose the wrong center, you can lose them. With proper center selection, all rays will be correctly displayed. On this basis, the size of the map I made is 2 times larger than the maximum length of the emitted rays.
The size of my card is 12 * 12 meters.

In fact, to solve this kind of problem, you can use any rangefinder.
A range finder is a device for determining the distance to something (in my case to a potential obstacle).
In robotics, mainly 2 types of rangefinders are used: ultrasonic and laser.
Ultrasonic range finders are much cheaper, but ultrasonic beams are wide enough and are not suitable for accurate measurements.
Laser rangefinders are more expensive, but more precisely, since their rays are narrowly directed.
To solve my problem, I used the Hokuyo URG-04LX-UG01 laser scanner. This sensor is capable of emitting beams at 240 ° and gives fairly accurate information about the obstacles that stand in the way of the beams. Its maximum range is 5-6 meters. It is worth noting that this rangefinder emits rays only in a 2D plane. This fact obliges to put the sensor on the robot in a certain place, usually in front of the bottom of the robot, to get a more accurate picture. Again, you can use 3D scanners, which provide much more accurate and complete information about the environment, but they are much more expensive.
I believe that this particular scanner is perfect for training in the price-quality ratio.

Hokuyo URG-04LX-UG01
Briefly about the principle of the laser scanner:
The range finder emits rays along the plane. The beam, which met an obstacle in its path, is reflected from it and comes back. From the phase difference between the signals sent and received, it is possible to judge how far the obstacle is located.
Accordingly, if the emitted beam did not return, then at 5–6 meters along its direct emission or there are no obstacles, or the beam could not correctly reflect.

The following data can be obtained from the laser scanner:
For each beam emitted:
* Each of the parameters is stored in a separate array and corresponds to the data for one of the rays.
To map the map and draw it, I used the ROS (Robot Operating System) tools, namely, the Rviz program and the data type nav_msgs :: OccupancyGrid. I created a publisher of a local map with the message type nav_msgs :: OccupancyGrid under the appropriate topic local_map. In Rviz, subscribing to this topic, took the data about the map and displayed them in the form of the type Map.
In accordance with this algorithm, it was necessary to programmatically adjust the processing of data from the laser scanner and record them in the required format for transmission. In OccupancyGrid, the map is stored and transmitted in a one-dimensional array.
Appeal to any element of such a one-dimensional array is as follows:
mapSize - local map size
j is the column number
i - line number
The map cells (again, according to the OccupancyGrid data type) should have values from 0 to 100. The smaller the value, the more likely it is that the cell is passable and vice versa.
To simplify the task, I have selected 3 primary colors for cell coloring.
An important point!
Before the arrival of data from the scanner, the map is completely unknown (the values of all cells = 50) and each time after drawing, it is again updated to an unknown state. This is done so that the map does not overlap with itself the extra, previous values. After all, the local map reflects the state of the environment only at a given time.

Unknown card
Rays are constructed using a transformation from the polar coordinate system (UCS)
to Cartesian coordinate system (DSC).
x, y - new coordinates in DSC
r - distance to the obstacle
φ is the angle at which the beam was dropped
r, φ - old coordinates in UCS
Fully pass through arrays of distances r and angles φ of rays (UCS data). For each item, do the following:

The simplest example of how a walkable path to an obstacle is built
Finally, the final touches!
Each card has permission. Simply put, this is the number of cells that can fit in 1 cell.
for example
If there is 1 cell in 1 cell (the simplest case), then the resolution is 1.
If there is 5 cells in 1 cell, then the resolution is 0.2.
My card resolution is 0.04. That is, there are 25 cells in each cell. Thus, my minimum step is 4 cm. And 1 cell is 1m.
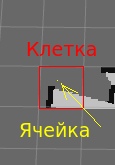
The difference of cells and cells on my map
An example of building a local cross-country map
* Yellow colors indicate cell colors.
I believe that, in general, the work I have done was successful, but I understand that the algorithm is imperfect and requires clarification and improvement.
In this publication I would like to talk about how I built a local map of patency for the robot. This task was necessary both to improve skills in programming and mastering sensors, and for the subsequent introduction of our own algorithms into the work of real robots at such robotic activities such as Robocross and Robofest.
This article is designed for those who are just entering the world of robotics or trying to figure out how to build a terrain map. I tried to present everything in the simplest and most understandable language that most people can understand.
What is a local cross-country map?
So, the local cross - country map is what the robot sees at a given time.
This is the information that comes from the “eye” of the robot and is subsequently processed and displayed in a convenient form.
')
If the robot is standing still, then its local map under constant environmental conditions remains constant.
If the robot moves, then at each moment of time its environment is different, respectively, the local map also changes.
A local map usually has a fixed size. The size is calculated based on the maximum length of the beams emitted by the rangefinder. In my case, this length is 6 meters.
To simplify the task, it was decided to make a square map. It was also decided that the range finder would be conventionally located exactly in the center of the map (this place would be the point where x = y = 0). The center was chosen in this way because the range finder that I use emits rays in the plane more than 180 ° (it emits rays at 240 °, but more on that later), that is, some rays will certainly go beyond the scanner and if you choose the wrong center, you can lose them. With proper center selection, all rays will be correctly displayed. On this basis, the size of the map I made is 2 times larger than the maximum length of the emitted rays.
The size of my card is 12 * 12 meters.

The sensor I used
In fact, to solve this kind of problem, you can use any rangefinder.
A range finder is a device for determining the distance to something (in my case to a potential obstacle).
In robotics, mainly 2 types of rangefinders are used: ultrasonic and laser.
Ultrasonic range finders are much cheaper, but ultrasonic beams are wide enough and are not suitable for accurate measurements.
Laser rangefinders are more expensive, but more precisely, since their rays are narrowly directed.
To solve my problem, I used the Hokuyo URG-04LX-UG01 laser scanner. This sensor is capable of emitting beams at 240 ° and gives fairly accurate information about the obstacles that stand in the way of the beams. Its maximum range is 5-6 meters. It is worth noting that this rangefinder emits rays only in a 2D plane. This fact obliges to put the sensor on the robot in a certain place, usually in front of the bottom of the robot, to get a more accurate picture. Again, you can use 3D scanners, which provide much more accurate and complete information about the environment, but they are much more expensive.
I believe that this particular scanner is perfect for training in the price-quality ratio.

Hokuyo URG-04LX-UG01
Briefly about the principle of the laser scanner:
The range finder emits rays along the plane. The beam, which met an obstacle in its path, is reflected from it and comes back. From the phase difference between the signals sent and received, it is possible to judge how far the obstacle is located.
Accordingly, if the emitted beam did not return, then at 5–6 meters along its direct emission or there are no obstacles, or the beam could not correctly reflect.

The following data can be obtained from the laser scanner:
For each beam emitted:
- Distance to obstacles
- Emission angle
* Each of the parameters is stored in a separate array and corresponds to the data for one of the rays.
About building a map
To map the map and draw it, I used the ROS (Robot Operating System) tools, namely, the Rviz program and the data type nav_msgs :: OccupancyGrid. I created a publisher of a local map with the message type nav_msgs :: OccupancyGrid under the appropriate topic local_map. In Rviz, subscribing to this topic, took the data about the map and displayed them in the form of the type Map.
In accordance with this algorithm, it was necessary to programmatically adjust the processing of data from the laser scanner and record them in the required format for transmission. In OccupancyGrid, the map is stored and transmitted in a one-dimensional array.
What's going on here?
For those who first encounter this type of ROS data: this is unusual, since the map is presented in a familiar way as a two-dimensional array with a certain number of columns and rows.
So it was with me. I store the map based on the data from the scanner in a two-dimensional array, and when forming a message to send to Rviz, I convert the two-dimensional array into a one-dimensional array, necessary for OccupancyGrid.
In fact, the map in OccupancyGrid is only stored and transmitted in a one-dimensional array. When decrypting its data, it will automatically turn into a square two-dimensional map.
But for this to happen correctly, it is necessary to record this one-dimensional array in a certain way.
Namely: line by line from the two-dimensional storage to write in one line.
Voila! This is the whole secret.
So it was with me. I store the map based on the data from the scanner in a two-dimensional array, and when forming a message to send to Rviz, I convert the two-dimensional array into a one-dimensional array, necessary for OccupancyGrid.
In fact, the map in OccupancyGrid is only stored and transmitted in a one-dimensional array. When decrypting its data, it will automatically turn into a square two-dimensional map.
But for this to happen correctly, it is necessary to record this one-dimensional array in a certain way.
Namely: line by line from the two-dimensional storage to write in one line.
Voila! This is the whole secret.
Appeal to any element of such a one-dimensional array is as follows:
mapSize - local map size
j is the column number
i - line number
The map cells (again, according to the OccupancyGrid data type) should have values from 0 to 100. The smaller the value, the more likely it is that the cell is passable and vice versa.
To simplify the task, I have selected 3 primary colors for cell coloring.
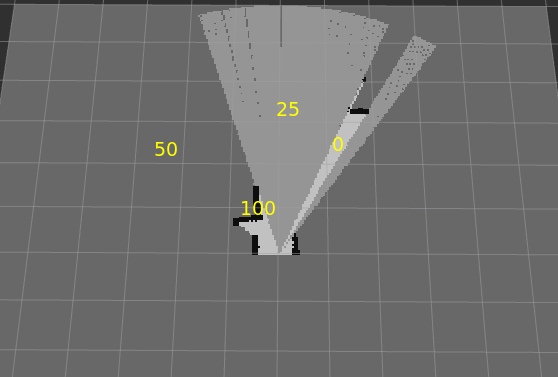
- White - passable zone = 0
- Black - impassable zone = 100
- Gray - unknown zone = 50
An important point!
Before the arrival of data from the scanner, the map is completely unknown (the values of all cells = 50) and each time after drawing, it is again updated to an unknown state. This is done so that the map does not overlap with itself the extra, previous values. After all, the local map reflects the state of the environment only at a given time.

Unknown card
Rays are constructed using a transformation from the polar coordinate system (UCS)
to Cartesian coordinate system (DSC).
$$ display $$ \ left \ {\ begin {gather} x = r * cos φ \\ y = r * sin φ \ end {gather} \ right. $$ display $$
x, y - new coordinates in DSC
r - distance to the obstacle
φ is the angle at which the beam was dropped
r, φ - old coordinates in UCS
Algorithm of data processing from the sensor:
Fully pass through arrays of distances r and angles φ of rays (UCS data). For each item, do the following:
- Convert the coordinates from the PSK to the DSC for the final r and φ. Paint the resulting cell black. This is an obstacle.
- We pass in a straight line from the location of the scanner to the cell with an obstacle with a certain step, in the simplest case equal to the size of the cell.
- Again, convert the data from the PSK to the DSC and paint the new cell in white. This is a passable zone.

The simplest example of how a walkable path to an obstacle is built
And what if the emitted beam did not return?
If this happens, it may mean the following:
* The “lost” beam can usually be because it did not reflect at an angle of 180 ° (that is, under any that did not reach back), since the obstacle could stand non-perpendicular to the beam. And as is known from physics: the angle of incidence is equal to the angle of reflection.

Or because the obstacle was too black and absorbed most of the energy of the beam and the beam did not have enough energy to go back.
Thus, it is impossible to be completely confident about what happened if the beam did not return.
What to do in such situations?
Do the following:
We do not lose anything, if the rays really did not encounter obstacles, and if some obstacle still escaped the “eyes” of the robot, then it will surely be detected very quickly.
- The beam was “lost”, that is, it was not fully reflected or was reflected in another direction.
- There were no obstacles in the path of the beam and because of this it simply had nothing to reflect
* The “lost” beam can usually be because it did not reflect at an angle of 180 ° (that is, under any that did not reach back), since the obstacle could stand non-perpendicular to the beam. And as is known from physics: the angle of incidence is equal to the angle of reflection.

Or because the obstacle was too black and absorbed most of the energy of the beam and the beam did not have enough energy to go back.
Thus, it is impossible to be completely confident about what happened if the beam did not return.
What to do in such situations?
Do the following:
- We consider the distance to the obstacle of such a beam as possible for the scanner (in our case it is 6 meters)
- We consider all the cells in a straight line to the obstacle to be semi-passable and assign them an intermediate number of 25. These are passable cells, but we are not completely sure of them.
We do not lose anything, if the rays really did not encounter obstacles, and if some obstacle still escaped the “eyes” of the robot, then it will surely be detected very quickly.
Card resolution
Finally, the final touches!
Each card has permission. Simply put, this is the number of cells that can fit in 1 cell.
for example
If there is 1 cell in 1 cell (the simplest case), then the resolution is 1.
If there is 5 cells in 1 cell, then the resolution is 0.2.
My card resolution is 0.04. That is, there are 25 cells in each cell. Thus, my minimum step is 4 cm. And 1 cell is 1m.

The difference of cells and cells on my map
What was the result?

An example of building a local cross-country map
* Yellow colors indicate cell colors.
I believe that, in general, the work I have done was successful, but I understand that the algorithm is imperfect and requires clarification and improvement.
Source: https://habr.com/ru/post/418585/
All Articles