Solving color Japanese crosswords at the speed of light

Japanese crosswords (also nonograms) are logical puzzles in which a pixel image is encrypted. Solve crossword need with the help of numbers located to the left of the rows and above the columns.

The size of the crossword puzzles can reach up to 150x150. The player with the help of special logical techniques calculates the color of each cell. The solution can take as little as a couple of minutes on beginner crossword puzzles, as well as dozens of hours on complex puzzles.

A good algorithm can solve the problem much faster. The text describes how to use the most appropriate algorithms (which generally lead to a solution), as well as their optimization and the use of C ++ features (which reduce the operating time by several dozen times) to write a solution that works almost instantly.

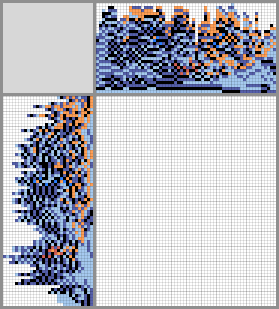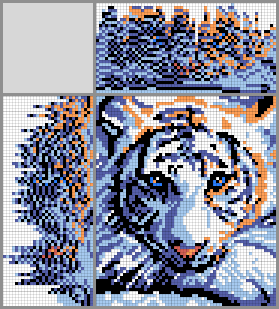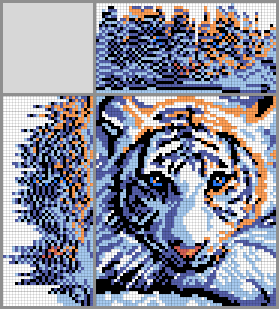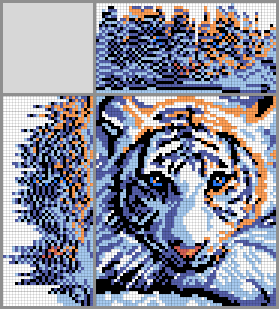
In the mobile version of Habr, formulas in the text may not be shown (not in all mobile browsers) - use the full version or another mobile browser if you notice problems with formulas

Rules of the game

Initially, the crossword canvas is white. For vanilla black and white crossword puzzles, you need to restore the location of black cells.

In black-and-white crossword puzzles, the number of numbers for each row (to the left of the canvas) or for each column (above the canvas) indicates how many groups of black cells are in the corresponding row or column, and the numbers themselves - how many fused cells each of these groups contains. Set of numbers $$$[3, 2, 5]$ means that in a certain row there are three consecutive groups of $$$3$ , $$$2$ and $$$5$ black cells in a row. Groups can be arranged in a row as horrible, without disturbing the relative order (numbers specify their length, and the position must be guessed), but they must be separated by at least one white cell.

Correct example

In color crosswords, each group still has its own color - any, except white, is a background color. Neighboring groups of different colors can stand close together, but for neighboring groups of the same colors, the separation of at least one white cell is necessary.

What is not a Japanese crossword

Each pixel image can be encrypted in the form of a crossword puzzle. But it can be impossible to restore it back - the resulting puzzle can either have more than one solution, or have one solution, but cannot be solved in a logical way. Then the remaining cells in the process of the game have to guess the shaman technology using quantum computers .

Such crosswords are not a crossword puzzle, but graphomania. It is believed that the correct crossword is such that in a logical way you can come to a single solution.

The "logical path" is the ability to restore each cell one by one, considering the row / column separately, or their intersection. If this is not possible, the number of considered answers can be very much, much more than a person can calculate.

Incorrect nonogram is the only solution, but it’s impossible to solve normally. Orange marked "unsolvable" cells. Taken from Wikipedia.

This limitation is explained in the following way: in the most general case, the Japanese crossword puzzle is an NP-complete task. However, guessing does not become an NP-complete task, if there is an algorithm, at each moment of time unambiguously indicating which cells to open further. All crossword puzzles used by humans (except for the method of Monte Carlo trial and error) are based precisely on this.

In the most Orthodox crossword puzzles, the width and height are divided by 5, there are no rows that can be counted instantly (such where either the colored cells fill all the spots or none at all), and the number of additional colors is limited. These requirements are not mandatory.

The simplest is the wrong crossword puzzle:

|1 1| --+---+ 1| | 1| | --+---+ 

Often, coded pixel art that uses "chess order" to simulate a gradient is not solved. It will be better to understand if you type in the search for "pixelart gradient". The gradient is just like this 2x2 file crossword puzzle.

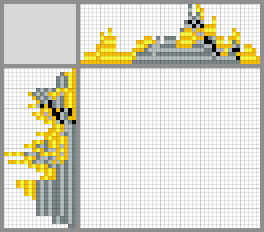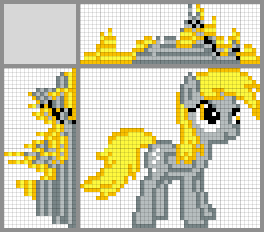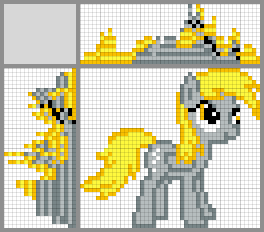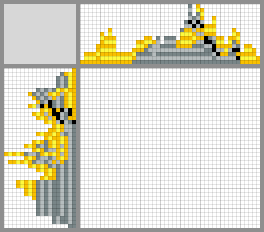
Possible solutions

We have the size of the crossword puzzle, the description of the colors and all the rows and columns. How can you collect from this picture:

Brute force

For each cell, we iterate over all possible states and check for satisfactory. The complexity of this solution for black and white crossword $$$O (N * M * {2} ^ {N * M})$ for color $$$O (N * M * {colors} ^ {N * M})$ . By analogy with the clown sorting, this solution can also be called clown. It is suitable for size 5x5.

Backtracking

All possible methods of arranging horizontal groups of cells are sorted out. We put a group of cells in a row, check that it does not break the description of groups of columns. If it breaks - we put further on 1 cell, we check again. Set - go to the next group. If the group cannot be put in any way - we roll back the two groups, rearrange the previous group, and so on, until we put the last group successfully.

Separately for each row

This solution is much better and truly true. We can analyze each row and each column separately. Each row will try to reveal the maximum information.

The algorithm for each cell in the row learns more information - it may turn out that it is impossible to paint the cell in some color, the groups will not converge. The row cannot be fully opened at once, but the information obtained “will help” several columns to open up better, and when we begin to analyze them, they again will “help” the rows, and this will take several iterations until all the cells have one possible color.

Truly the right decision

One line, two colors

Effective guessing of a black-and-white one-line player, for which some cells have already been guessed, is a very tough task. She met in places like:

• The quarter-finals of ACM ICPC 2006 - you can try to solve the problem yourself . The time limit is 1 second, the number of groups is limited to 400, and the row length is also 400. It has a very high level of complexity compared to other tasks.
• International Olympiad in Informatics 2016 - condition , pass the task . Time limit 2 seconds, limiting the number of groups to 100, the length of the row 200'000. Such constraints are overkills, but solving the problem with ACM constraints is 80/100 points in this task. Here, too, the level did not disappoint, schoolchildren from around the world with a cruel level of IQ are trained for several years to solve different tin, then go to this Olympiad (only 4 people from the country have to go), decide 2 rounds of 5 hours and in the case of epic win (bronze in different years for 138-240 points out of 600) entering Oxford, then offers from clear companies to the search department, a long and happy life embracing with dakimama.

A monochrome one-liner can also be solved in different ways, and for $$$O (N * 2 ^ N)$ (enumeration of all variants, check for correctness, selection of cells that have the same color in all variants), and still somehow less stupid.

The basic idea is to use an analogue backtracking, but without unnecessary calculations. If we have somehow put several groups and are now in a certain cell, then it is required to find out whether it is possible to put the remaining groups, starting with the current cell.

 def EpicWin(group, cell): if cell >= last_cell: #   return group == group_size win = False #        if group < group_size #    and CanInsertBlack(cell, len[group]) #    and CanInsertWhite(cell + len[group], 1) #    and EpicWin(group + 1, cell + len[group] + 1): #    win = True can_place_black[cell .. (cell + len[group] - 1)] = True can_place_white[cell + len[group]] = True; #         if CanInsertWhite(cell, 1) and EpicWin(group, cell + 1): win = True can_place_white[cell] = True return win EpicWin(0, 0) 

This approach is called dynamic programming . The pseudocode is simplified, and there even the memorization of the calculated values ​​is not performed.

The functions CanInsertBlack/CanInsertWhite are needed to check whether it is theoretically possible to put the group of the desired size in the right place. All they have to do is to check that there is no “100% white” cell in the specified cell range (for the first function) or “100% black” (for the second). So they can work for $$$O (1)$ , this can be done using partial sums:

 white_counter = [ 0, 0, ..., 0 ] #   n def PrecalcWhite(): for i in range(0, (n-1)): if is_anyway_white[i]: # 1,  i-  100%  white_counter[i]++ if i > 0: white_counter[i] += white_counter[i - 1] def CanInsertBlack(cell, len): #     [cell, cell + len - 1] ans = white_counter[cell + len - 1] if cell > 0: ans -= white_counter[cell - 1] #  ans -     cell  (cell + len - 1) return ans == 0 

The same witchcraft with partial sums is waiting for a string like

 can_place_black[cell .. (cell + len[group] - 1)] = True 

Here, instead of = True , you can increase the number by 1. And if we need to make many additions on a segment in a certain array $$$array$ and, moreover, we don’t use this array before various additions (they say about this that this task is “solved offline”), instead of a cycle:

 #     for i in range(L, R + 1): array[i]++ 

You can do this:

 #     array[L]++ array[R + 1]-- #    for i in range(1, n): array[i] += array[i - 1] 

Thus, the whole algorithm works for $$$O (k * n)$ where $$$k$ - the number of groups of black cells, $$$n$ - string length. And we go to the ACM ICPC semifinal or get the internum bronze. ACM solution (Java) . IOI solution (C ++) .

One row, many colors

When switching to multi-color nonograms, which are still not clear how to solve, we will know the terrible truth - it turns out that every column has a magical effect on all the columns! This is clearer through an example:

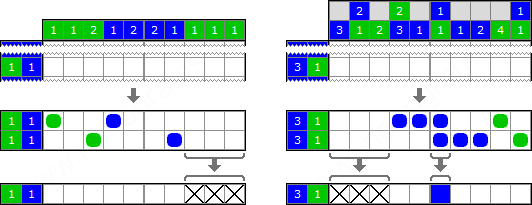
Source - Methods for solving Japanese crosswords

While the two-color nonograms normally did without it, they did not need to look back at orthogonal friends.

The picture shows that in the left-hand example the three rightmost cells are empty because the configuration will break if we paint these cells in those colors in which to dye yourself non-white color.

But this joke is mathematically resolvable - each cell should be given a number, where $$$i$ th bit will mean whether you can give this cell $$$i$ th color Initially, all cells have a value of $$$2 ^ {colors} - 1$ . The solution dynamics will not change very much.

It will be possible to observe the following effect: in the same left-hand example, according to the row version, the rightmost cell can have either blue or white color.

According to the column version, this cell is either green or white.

According to the common sense version, this cell will have only white color. And then we continue to calculate the answer.

If we assume the zero bit is "white", the first is "blue", the second is "green", then the line calculated the state for the last cell $$$011$ and column $$$101$ . So, in fact, this cell has a state $$$011 \ & 101 = 001$

 source = [...] #   result = [0, 0, ..., 0] #   len = [...] #    clrs = [...] #    def CanInsertColor(color, cell, len): for i in range(cell, cell + len): if (source[i] & (1 << color)) == 0: #     color    return False; return True def PlaceColor(color, cell, len): for i in range(cell, cell + len): result[i] |= (1 << color) #   color  OR def EpicWinExtended(group, cell): if cell >= last_cell: #   return group == group_size win = False #        if group < group_size #    and CanInsertColor(clrs[group], cell, len[group]) #    and SequenceCheck() #       ,  #         and EpicWin(group + 1, cell + len[group]): #    win = True PlaceColor(clrs[group], cell, len[group]) PlaceColor(0, cell + len[group], 1) #   -    #         #   -  0 if CanInsertWhite(0, cell, 1) and EpicWinExtended(group, cell + 1): win = True PlaceColor(0, cell, 1) return win 

Many rows, many colors

Constantly doing the update of the states of all rows and columns, described in the last paragraph, until there is a single cell with more than one bit. In each iteration, after updating all rows and columns, we update the states of all cells in them through mutual AND.

First results

Suppose we wrote the code not as woodpeckers, that is, we don’t copy objects anywhere by mistake instead of passing by reference, we don’t invent bicycles anywhere in the algorithm, use __builtin_popcount and __builtin_ctz ( gcc features ) for bit operations, everything is neat and clean.

Let's look at the time of the program, which reads the puzzle from the file and solves it completely. It is worth assessing the merits of a machine on which all this stuff was written and tested:

 RAM - 4GB  - AMD E1-2500,  1400MHz  L1 - 128KiB, 1GHz  L2 - 1MiB, 1GHz  - 2,  - 2   « SoC   »   2013    28  

It is clear that such a supercomputer was chosen, because optimizations on it have a greater effect than on a flying shaitan-machine.

So, after running our algorithm on the most difficult crossword (according to nonograms.ru), we get a not very good result - from 47 to 60 seconds (this includes reading from the file and the solution). It should be noted that the "complexity" on the site is well calculated - the same crossword in all versions of the program was also the hardest, the other most difficult crosswords in the opinion of the archive were kept in the top in time.

Color Crossword №9596, the greatest difficulty

For quick testing, the benchmark functionality was made. To obtain data for him, I sparsil 4683 color crosswords (out of 10906 ) and 1406 black-and-whites (out of 8293 ) with nonograms.ru (this is one of the largest nonogram archives on the Internet) and saved them in a format understandable to the program. We can assume that these crosswords are a random sample, so the benchmark would show adequate average values. Also, the numbers of the pair of dozens of the most "difficult" crosswords (also the largest in size and number of colors) are written into the script for handles.

Optimization

Here are possible techniques for optimization that were made (1) at the time of writing the entire algorithm, (2) for shrinking the operation time from half a minute to fractions of a second, (3) those optimizations that may be useful further.

At the time of writing the algorithm

• Special functions for bit operations, in our case __builtin_popcount for counting the units in the binary notation, and __builtin_ctz for the number of zeros before the first youngest unit. Such functions may not appear in some compilers. For Windows, suitable analogs are:

 #ifdef _MSC_VER # include <intrin.h> # define __builtin_popcount __popcnt #endif 

• Array organization - the smaller size is at the beginning. For example, it is better to use the array [2] [3] [500] [1024] than [1024] [500] [3] [2].
• The most important thing is the general adequacy of the code and the avoidance of unnecessary worries for calculations.

What reduces the work time

• -O2 flag when compiling.
• In order not to re-throw a completely solved row / column into the algorithm, you can in the separate std :: vector / array start the flags for each row, mark them with a complete decision, and stop them from going further if there is nothing to decide.
• The specificity of a multi-repetition problem solving for dynamics suggests that a special array that contains flags marking the already “computed” pieces of the problem should be reset every time with a new solution. In our case, this is a two-dimensional array / vector, where the first dimension is the number of groups, the second is the current cell (see the EpicWin pseudocode from above, where this array is not, but the idea is clear). Instead of zeroing, you can do this — let us have a “timer” variable, and the array consists of numbers that show the last “time” when this piece was recalculated last. When starting a new task, the "timer" is incremented by 1. Instead of checking the Boolean flag, check the equality of the array element and the "timer". This is effective especially in cases where not all possible states are covered by the algorithm (which means that resetting the array, "have we already considered this" takes a healthy chunk of time).
• Replacing simple operations of the same type (assignment cycles, etc.) with analogues in STL or more adequate things. Sometimes it works faster than a bike.
• std::vector<bool> in C ++ compresses all Boolean values ​​to individual bits in numbers, which works on access a little slower than if it were a normal value at an address. If the program is very, very often refers to such values, then replacing the bool with an integer type can well affect performance.
• The remaining weaknesses can be searched through profilers and edit them. I myself use Valgrind, its performance analysis is convenient to look through kCachegrind. Profilers are built into many IDEs.

These edits were enough to get such data on the benchmark:

 izaron@izaron:~/nonograms/build$ ./nonograms_solver -x ../../nonogram/source2/ -e [2018-08-04 22:57:40.432] [Nonograms] [info] Starting a benchmark... [2018-08-04 22:58:03.820] [Nonograms] [info] Average time: 0.00497556, Median time: 0.00302781, Max time: 0.215925 [2018-08-04 22:58:03.820] [Nonograms] [info] Top 10 heaviest nonograms: [2018-08-04 22:58:03.820] [Nonograms] [info] 0.215925 seconds, file 9596 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.164579 seconds, file 4462 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.105828 seconds, file 15831 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.08827 seconds, file 18353 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.0874717 seconds, file 10590 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.0831248 seconds, file 4649 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.0782811 seconds, file 11922 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.0734325 seconds, file 4655 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.071352 seconds, file 10828 [2018-08-04 22:58:03.820] [Nonograms] [info] 0.0708263 seconds, file 11824 

 izaron@izaron:~/nonograms/build$ ./nonograms_solver -x ../../nonogram/source/ -e -b [2018-08-04 22:59:56.308] [Nonograms] [info] Starting a benchmark... [2018-08-04 23:00:09.781] [Nonograms] [info] Average time: 0.0095679, Median time: 0.00239274, Max time: 0.607341 [2018-08-04 23:00:09.781] [Nonograms] [info] Top 10 heaviest nonograms: [2018-08-04 23:00:09.781] [Nonograms] [info] 0.607341 seconds, file 5126 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.458932 seconds, file 19510 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.452245 seconds, file 5114 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.19975 seconds, file 18627 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.163028 seconds, file 5876 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.161675 seconds, file 17403 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.153693 seconds, file 12771 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.146731 seconds, file 5178 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.142732 seconds, file 18244 [2018-08-04 23:00:09.781] [Nonograms] [info] 0.136131 seconds, file 19385 

You can see that, on average, black and white crosswords are "more difficult" than color. This confirms the observations of game lovers, who also believe that the "color" are solved on average easier.

Thus, without radical revisions (such as rewriting the entire code to C or assembly inserts with fastcall and lowering the frame pointer) can be achieved by high performance, we note, on a very modest computer. The Pareto principle can be applied to optimizations - it turns out that small optimization influences strongly because this piece of code is critical and is called very often.

Further optimization

The following methods can greatly improve program performance. Some of them work not in all cases, but under certain conditions.

• Rewriting code in C-style and other year 1972. Replace ifstream with sishny analog, vectors with arrays, learn all the compiler options and fight for each processor clock.
• Parallelization. For example, in the code there is a piece where the rows are sequentially updated, then the columns:

  ... if (!UpdateGroupsState(solver, dead_rows, row_groups, row_masks)) { return false; } if (!UpdateGroupsState(solver, dead_cols, col_groups, col_masks)) { return false; } return true; 

These functions are independent of each other and they do not have shared memory except for the variable solver (OneLineSolver type), so you can create two "solver" objects (only one is obvious here - solver) and run two threads in the same function. The effect is the same: in color crosswords, the “hardest” is solved twice as fast, in black and white the same one third faster, and the average time has increased, due to the relatively high costs of creating streams.

But in general, I would not advise doing it right in the current program and using it calmly - first, creating threads is a costly operation, you should not constantly create threads for microsecond tasks, and second, with some combination of program arguments, threads can access simultaneously - external memory, for example, when creating image solutions - this should be taken into account and secured.

If the task were serious and I would have a lot of data and multi-core machines, I would go even further - you can start several constant streams, each will have its own OneLineSolver object, and another thread-safe structure that drives the distribution of work and upon request it gives a reference to the next row / column for the solution. Flows after solving the next task turn to the structure again to solve something else. In principle, some nonogram problem can be solved without completing the previous one, for example, when this structure deals with the mutual AND of all cells, and then some flows are free and do nothing. Another parallelization can be done on the GPU through CUDA - there are many options.

• Using classic data structures. Please note - when I showed pseudocode solutions for colored nonograms, the functions CanInsertColor and PlaceColor do not work for $$$O (1)$ , unlike black and white nonograms. It looks like this in the program:

 bool OneLineSolver::CanPlaceColor(const vector<int>& cells, int color, int lbound, int rbound) { // Went out of the border if (rbound >= cells.size()) { return false; } // We can paint a block of cells with a certain color if and only if it is // possible for all cells to have this color (that means, if every cell // from the block has color-th bit set to 1) int mask = 1 << color; for (int i = lbound; i <= rbound; ++i) { if (!(cells[i] & mask)) { return false; } } return true; } void OneLineSolver::SetPlaceColor(int color, int lbound, int rbound) { // Every cell from the block now can have this color for (int i = lbound; i <= rbound; ++i) { result_cells_[i] |= (1 << color); } } 

That is, it works for the line, for $$$O (N)$ (Later there will be an explanation of the meaning of such a code).

Let's see how you can get the best difficulty. Take CanPlaceColor . This function checks that among all the numbers of the vector in the segment $$$[lbound, rbound]$ bit number $$$color$ set to 1. Equivalent to this you can take $$$AND$ of all numbers of this segment and check bit number $$$color$ . Using the fact that the operation $$$AND$ commutative , as well as the sum, minimum / maximum, product, or operation $$$XOR$ for quick counting $$$AND$ of the entire segment, you can use almost any data structure that works with commutative operations on the segment. It:

1. SQRT decomposition. Pre-count $$$O (\ sqrt {N})$ , request $$$O(\sqrt{N})$ . .
2. . $$$O(N\log{N})$ , $$$O(\log{N})$ . .
3. (Sparse Table). $$$O(N\log{N})$ , $$$O (1)$ . .

, - ( $$$O(N)$ , $$$O (1)$ ) , , , $$$\varphi$ , $$$\varphi(\alpha, \beta) \in \{\alpha, \beta\}$ , — (, ...)

SetPlaceColor . . SQRT- ( " "). - .

- — .

, — , ? :

1. . $$$\log$ , , — ( magic number , ). , $$$N=10^{5}$ , $$$O(N^2)$ 10 , $$$O(N\log{N})$ 0.150 , $$$N$ , . , ( ): $$$O(N\sqrt{N})$ versus $$$O(N\log^2{N})$ . $$$N$ ( ) — 15-30.
2. , .

— , - — $$$N$ , . , ~25% ~11% , . - , , , .

— , . .

• . , , - . : , , "" ? , , ! . , .
• (, 1337 1000x1000) . std::bitset , — , .

, . "" . , C++ ( rope , ), hashtable , 3-6 / 4-10 /, unordered_map. , boost.

ROFL Omitting Format Language

, , , -.

ROFL — , "GNU's Not Unix". , , , , , . Omitting — (, , : — ).

, Matroska — 4 [52][4F][46][4C], , , , 3 , — , .

, MIT, — , .

Sources

GitHub . , , (, ). Magick++ args .

, ( ). nonograms.ru , , .

nonograms.ru .. KyberPrizrak , , , ! nonograms.ru, .

.