Pythagorean mathematical substantiation of the musical scale
The venerable Pythagoras rejected the evaluation of music based on the evidence of feelings. He argued that its virtues should be perceived by the mind, and therefore judged music not by ear, but on the basis of mathematical harmony and found it sufficient to limit the study of music to the limits of one octave.
Plutarch
')
Strictly speaking, the discussion here will be about the Pythagorean system. What is gamma and build in music?
Gamma , or sound sequence, is a sequence of sounds (steps) of a certain musical system (fret), located, starting from the main sound (pitch), in ascending or descending order. The name "gamma" comes from the Greek letter Gγ (gamma), which in the Middle Ages was designated as the extreme lower tone of the scale, and then the whole scale.
The most important characteristic of a musical sound is its height , which is a reflection in the consciousness of the frequency of oscillation of a sounding body, for example, a string. The higher the oscillation frequency of the string, the “higher” the sound seems to us.
Each single sound does not form a music system and, if it is not too loud, it does not cause us a special reaction. However, the combination of two sounds in other cases is pleasant and harmonious, while in others, on the contrary, it “cuts” the ear. A consistent combination of two sounds is called a consonance , an inconsistent one is a dissonance . It is clear that the consonance or dissonance of two tones is determined by the altitude distance between these tones or spacing.
The interval between two tones is the sequence number of the upper tone stage relative to the lower one in the given scale, and the interval coefficient I 21 of two tones is the ratio of the frequency of the upper tone oscillations to the lower frequency * :
 (6.1)
(6.1)* ( In music theory, the concepts of interval and interval coefficient are not strictly delimited. Following the tradition, we often call interval interval for brevity. )
Consider now a certain set of sounds, pressing, for example, on the piano several keys in sequence. Most likely, we will have an incoherent set of sounds, as they say, neither in the warehouse nor in the mood. In other cases, the sounds seem to fit, get along with each other, but their combination will seem torn, incomplete. I would like to continue this sequence to a certain note, which in this system of sounds seems to be the most stable, the main one and is called tonic . So, the sounds in the musical system are interconnected by certain dependencies, some of them are unstable and are resistant to others - stable .
But not only tonic and a set of stable and unstable sounds determine the nature of the musical system. It is easy to see by pressing eight white keys in succession from the note to (gamma in natural major ) and from the note la (in natural minor ) that these scales sound different: the first - major - sounds cheerful and light, and the second - minor - sad and overcast * . Consequently, there is another characteristic of the sound system - inclination: major or minor. Thus, we come to one of the most complex concepts in music theory - the concept of fret.
* (The nature of the sound of the harmony, of course, is not so rude and unequivocal. This question is very delicate, and we'll talk about it at the end of the chapter. )
Ladom is a pleasant for hearing interconnection of musical sounds, determined by the dependence of unstable sounds on stable ones, and above all on the main stable sound - tonic, and having a certain character of sounding - inclination. The history of musical culture knows a lot of ways characteristic of different nations and different times. The ancient Greeks knew a dozen frets, and the frets of some eastern countries and India are extremely complex, original and unusual for European hearing. The most common modern frets consist of seven basic steps, each of which can be raised or lowered, which gives five additional sounds. Thus, the diatonic (7-step) gamma-lada turns into chromatic (12-sound). The first step of the fret is tonic. The laws of the structure of the harmony is a whole science, the cornerstone of musicology, and many scientists and composers have devoted their entire lives to the study of these laws.
We will be primarily interested in mathematical laws describing the structure of the mode, that is, the musical system. The musical system is the mathematical expression of a certain system of pitch relationships. In addition to purely theoretical interest, the system finds application in tuning musical instruments with fixed pitch sounds, such as piano or organ.
In conclusion, we note that our experiments with keystrokes on the piano can end in the rarest and most pleasant phenomenon, when the sound system taken will not only belong to any scale, but will also be meaningful. Such an artistically meaningful series of sounds of different heights is called a melody . This is what we love to hum so much, depending on our mood - vigorous, sad, cheerful ...
After such a brief excursion into theoretical musicology, we can return to the shores of sunny Hellas in the times of the wise Pythagoras. Let us try to restore the reasoning of Pythagoras and his students in building the Pythagorean system, for it was this system that determined for thousands of years, if not forever, the whole development of musical culture, not only European, but also eastern. Pythagoras himself did not leave any written work, and the legacy of the Pythagoreans seems to be a hopeless heap of ruins, that is, a collection of accidentally surviving fragments and later quotations. Undoubtedly, these ruins are beautiful and still amaze the ruins of the famous Parthenon, but much of these fragments are lost without a trace and one can often only guess about the whole. And still…
Monochord - single-string - was one of the first musical instruments of the ancient Greeks. It was a long box, necessary to enhance the sound, over which the string was stretched. From the bottom, the string was pressed by a movable stand for dividing the string into two separate sounding parts. On the wooden box under the string there was a scale of divisions, which made it possible to establish exactly what part of the string sounds. Of course, as a musical instrument, the monohord will seem to us too primitive, but it was an excellent physical instrument and textbook on which ancient contemplators comprehended the wisdom of musical literacy.
The ancients claimed that Pythagoras already knew the laws of the oscillation of a monochord string and the construction of musical consonances (consonances), but we find a record of these laws in Pythagorean Archit from Tarente (428-365 BC), who lived Pythagoras a century and a half later . Architect was, of course, the most prominent representative of the Pythagorean school, a friend of the philosopher Plato and a teacher of mathematician Eudox (ca. 408 - ca. 355 BC), a statesman and commander. Archit's versatility is striking: he solved the famous de-cube problem of doubling a cube, was deservedly considered the greatest Pythagorean music theorist, first organized the mechanics based on mathematics and reduced the movements of mechanisms to geometric drawings, worked on the wooden model of a flying pigeon. According to van der Waerden, Archit is the author of the Eighth book “The Beginnings” of Euclid, which sets forth the arithmetic theory of proportions. As a statesman, Archit enjoyed exceptional respect: he was elected strategist for seven years in a row * , although by law strategists were elected only for one year. Archid rescued Plato from captivity by skillful diplomatic maneuvers and thus saved the life of the great philosopher. "The glorious Archit, the land, and the seas, and the sand, the numerator ..." - wrote Horace.
* ( Strategist - in the ancient Greek city-states a warlord, clothed with extensive military and political powers. )
“The laws of Pythagoras - Archite”, on which the whole Pythagorean theory of music was based, can be formulated as follows:
1- The pitch (oscillation frequency f) of the sounding string is inversely proportional to its length l:
 (6.2)
(6.2)here a is the proportionality coefficient depending on the physical properties of the string (thickness, material, etc.).
2. Two sounding strings give consonance only when their lengths are referred to as integers that make up the triangular number 10 = 1 + 2 + 3 + 4, i.e., as 1: 2, 2: 3, 3: 4.
These intervals are “perfect consonances,” and their interval coefficients were later given Latin names * :
* ( The names of intervals in music are Latin numerals, which indicate the ordinal number of the degree of the scale, constituting the interval with the original degree: octave - the eighth, fifth - fifth, fourth - fourth, etc. )
octave
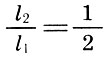
quint
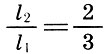
quart

Triangular number 10
It was also noted that the most complete fusion of tones gives an octave (2/1), followed by a fifth (3/2) and a quarte (4/3), i.e. the smaller the number n with respect to the form 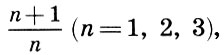 the consonant interval.
the consonant interval.
"The second law of Pythagoras - Archita" and now it seems surprising. What to say about the Pythagoreans, whom he simply delighted! Here they found confirmation of their entire philosophy: whole numbers, moreover, the numbers of the tetractys rule everything, even music! The Pythagoreans were not long in coming and spread the law of musical relations wherever possible, including the structure of the universe.
So, if we take a segment l equal to 1/12 of the length of a monochord l 1 as the price of dividing the scale of a monochord, then along with the entire string of monochord of length l 1 = 12l its parts of length l 2 = 6l will sound like an octave higher (l 2 / l 1 = l / 2), l 3 = 9l - sound per quint higher (l 3 / l 1 = 2/3) and l 4 = 8l - sound one quart higher (l 4 / l 1 = 3/4 ). This consonance and the numbers 6, 8, 9, 12 that define it were called the tetrad (four). The Pythagoreans believed that the tetrad was “the scale that sirens sang.” When tuning the ancient lyre, which became the symbol of music, its four strings were necessarily tuned according to the tetrad rule, and the tuning of the other strings depended on the fret in which it was to play on it.
But for the ancient thinker it was not enough to establish the numerical values of the quantities being studied. The Pythagorean eye and mind are not only accustomed to measure, but also to measure, that is, to reveal the internal connections between the objects under study, in other words, to establish proportional relations. Archit was a true Pythagorean, and he established proportional relations between the main perfect consonance — the octave, the quint, and the quarte. This decision was received by Archite in connection with the desire to divide the octave into melodious intervals. Probably, Archite proceeded from the intuitively obvious assumption that, along with the f 1 and f 2 = 2f 1 tones, giving the main consonance - the octave, should give the consonance and their arithmetic average f 3 = (f 1 + f 2 ) / 2. But then the length of the string l 3 is expressed in terms of the lengths of the strings l 1 and l 2 according to (6.2) as follows:
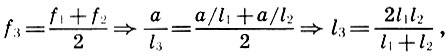
that is, l 3 is the harmonic mean of l 1 and l 2 (see 5.1). It is easy to detect the reverse: the harmonic mean for the frequencies f 1 and f 2 goes into the arithmetic mean for the lengths l 1 and l 2 :

Remembering that 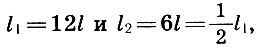 Together with Archy we come to an important conclusion:
Together with Archy we come to an important conclusion:
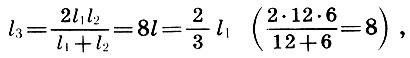 (6.3)
(6.3)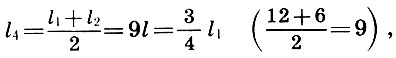 (6.4)
(6.4)that is, the quint is the harmonic average of the pitch lengths l 1 and octaves l 2 , and a quart is the arithmetic average l 1 and l 2 .
But the product of the arithmetic mean and the harmonic mean is equal to the product of the original numbers:
 (6.5)
(6.5)whence, dividing both parts by l 1 2 , we obtain the second important conclusion:
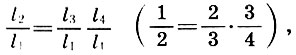 (6.6)
(6.6)or
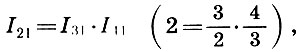
i.e., an octave is the product of a fifth by a quart.
By dividing (6.5) into l 1 l 3 , Archit also gets a third of the basic proportions — geometric:
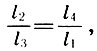 (6.7)
(6.7)which was called "musical": the octave refers to the quinte as a quart to the basic tone .

The division of a monochord string (l 1 ) into parts that form perfect consonances with it: an octave (l 2 ), a fifth (l 3 ) and a quarte (l 4 ) and the relations between them. The intervals that the whole monochord string forms with its parts are shown by red arrows.
It is easy to get two more relationships:
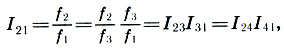 (6.8)
(6.8)that is, the octave is divided into two unequal consonance intervals — the fifth and the fourth . The interval that complements this interval to an octave is called its reference . Thus, the fifth is the circulation of the quarte and vice versa.
Finally, we find the interval coefficient between the strings of the quinte l 3 and quarts l 4 , which, together with its interval, is called the tone (do not confuse the tone-interval and the tone-sound of a given height):
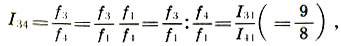 (6.9)
(6.9)that is, the tone interval is equal to the ratio of the fifth to the fourth .
Note that, in contrast to the usual distance on a straight line, r 21 = x 2 - x 1 defined as the difference between the coordinates of the end and the beginning, the interval coefficient — the altitude distance — is defined as the ratio of its constituent tones 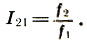 Then three tones f 1 <f 2 <f 3 , located at equal distances r and forming an arithmetic progression x 1 , x 2 = x 1 + r, x 3 = x 1 + 2r. Therefore, the interval coefficients are added and subtracted "geometrically", and the intervals themselves - "arithmetically", as usual distances, namely:
Then three tones f 1 <f 2 <f 3 , located at equal distances r and forming an arithmetic progression x 1 , x 2 = x 1 + r, x 3 = x 1 + 2r. Therefore, the interval coefficients are added and subtracted "geometrically", and the intervals themselves - "arithmetically", as usual distances, namely:
the sum of two intervals is equal to the product of their interval coefficients:
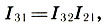 (6.10)
(6.10)the difference between the two intervals is equal to the quotient of their interval coefficients:
 (6.11)
(6.11)divide the interval into n equal parts means to extract the root of degree n from its interval coefficient:
 (6.12)
(6.12)etc.
To go from interval coefficients to intervals-distances, it is enough to enter the logarithmic interval L = log a I and the logarithmic frequency F = log a f. Then, logarithmizing the definition (6.1) and equalities (6.10) - (6.12), we get the usual definition and rules of action with distances:
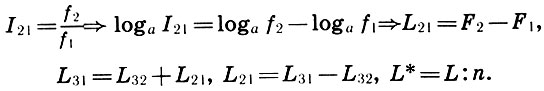 (6.13)
(6.13)The solution to the problem of dividing the octave prompted Archit at once to two proofs of irrationality. 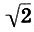 . In fact, if we try to divide the octave into two equal intervals I, then, assuming in (6.8) I 23 = I 31 = I, we have
. In fact, if we try to divide the octave into two equal intervals I, then, assuming in (6.8) I 23 = I 31 = I, we have

But with such a ratio of string lengths there is a clear discord. Since the consonance is determined by the ratio of integers of the form (n + 1): 2, the thought suggests itself that the number 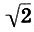 can not be expressed by the ratio of two integers, that is, is irrational.
can not be expressed by the ratio of two integers, that is, is irrational.
Second proof of irrationality 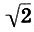 less musical but more mathematic. To find the square root of a number that is not a complete square, Archite decomposes it into two unequal factors (2 = 1 * 2), then forms an arithmetic average of 3/2 and a harmonic average of 4/3 of these factors and makes up the musical proportion of these numbers ( 6.7):
less musical but more mathematic. To find the square root of a number that is not a complete square, Archite decomposes it into two unequal factors (2 = 1 * 2), then forms an arithmetic average of 3/2 and a harmonic average of 4/3 of these factors and makes up the musical proportion of these numbers ( 6.7):
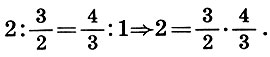
The product of the average terms of this proportion is equal to the given number 2, and their difference  less than the difference of the zero approximation 2 - 1 = 1. Therefore,
less than the difference of the zero approximation 2 - 1 = 1. Therefore,  can be considered as approximate values
can be considered as approximate values 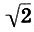 .
.
(3/2 with excess, 4/3 with deficiency].
Doing the same procedure over the first approximations, we obtain the second approximations:

where
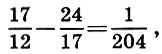
and then the third approximations:
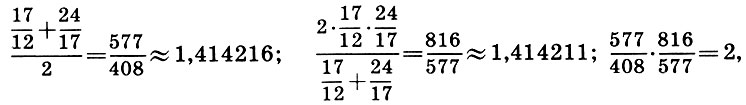
where
1.414216-1.414211 = 0.000005.
Since this procedure can be repeated indefinitely, it is clear that the number 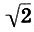 irrational. Along the way, we are convinced of the justice of the Pythagorean idea that the greater the integer numbers in a relation, the more accurately they express the irrational number (see p. 96). Finally, remembering what the value
irrational. Along the way, we are convinced of the justice of the Pythagorean idea that the greater the integer numbers in a relation, the more accurately they express the irrational number (see p. 96). Finally, remembering what the value 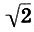 equal to 1.414213 ..., we see that the “musical” method of Archit very quickly converges to the exact value
equal to 1.414213 ..., we see that the “musical” method of Archit very quickly converges to the exact value 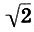 and the third approximation gives five correct signs after the comma!
and the third approximation gives five correct signs after the comma!
But back to our intervals. So, the octave is divided into two unequal consonances of a fifth and a quarte, and a fifth is divided into a consonance of quarte and a tone of discord. The tone-interval was taken as the interval between the next-highest sounds (steps) when building the Pythagorean scale. Here is the key to building a fret. In the opinion of the Soviet musicologist L. A. Mazel, the interval of the fifth, divided into quarts and tones, is the main musical element. Having chosen the tone as the main lad-forming step, the ancient theorists need only to postpone the main sound  then another tone
then another tone  , and the remaining interval between the second tone and the quart tone
, and the remaining interval between the second tone and the quart tone 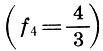 call a semitone
call a semitone 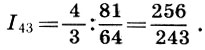 The name is quite justified, since the division of the tone-interval in half by the formula (6.12) gives
The name is quite justified, since the division of the tone-interval in half by the formula (6.12) gives 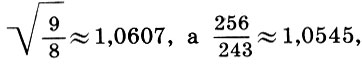 that is, the semitone is almost half the tone * . Thus was obtained the basis of all ancient Greek music - the tetrachord - a four-stringed scale within a quart.
that is, the semitone is almost half the tone * . Thus was obtained the basis of all ancient Greek music - the tetrachord - a four-stringed scale within a quart.
* (The interval of tone (semitone) in music theory is taken as the unit of arithmetic measurement of intervals, and the intervals of tone and semitone, in contrast to their interval coefficients, are called long and short seconds. )
It is clear that there are only three possibilities for the position of a semitone within the tetrachord, which determined the character and the name of the tetrachord:
Dorian: semitone - tone - tone;
Phrygian: tone - semitone - tone;
Lydian: tone - tone - semitone .
The names of the tetrachords indicate the corresponding regions of Greece and Asia Minor, each of which sang in its own way.
Of course, the four strings within a quart were few for conducting the melody, so the tetrachords were connected. We have already found out that the octave consists of two quarts and a tone; therefore, two tetrachords can be placed within an octave, separated by a tone interval. Combining the two tetrachords of the same name with the help of a separating tone, they got an octave, which the Greeks called “harmony”. It was in the ancient theory of music that the word "harmony" found its modern meaning - the consent of the disagreeable. There were three such main types of harmony in the number of tetrachords:

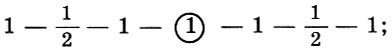

Here 1 means tone, 1/2 means semitone, the separation tone is circled. These antique harmonies are comparable to modern scales. In fact, everyone familiar with the basics of musical literacy learns in Lydian harmony the usual natural major (2 tones - semitone, 3 tones - semitone, or on the white piano keys to - re - mi - f - salt - la - c - until ), and in the Dorian and Phrygian - almost natural minor * .
* ( “Almost” because in comparison with the natural minor (1 - 1/2 - 1 - 1 - 1/2 - 1 - 1), the second step is reduced in the Dorian range, and the sixth in the Phrygian range. )
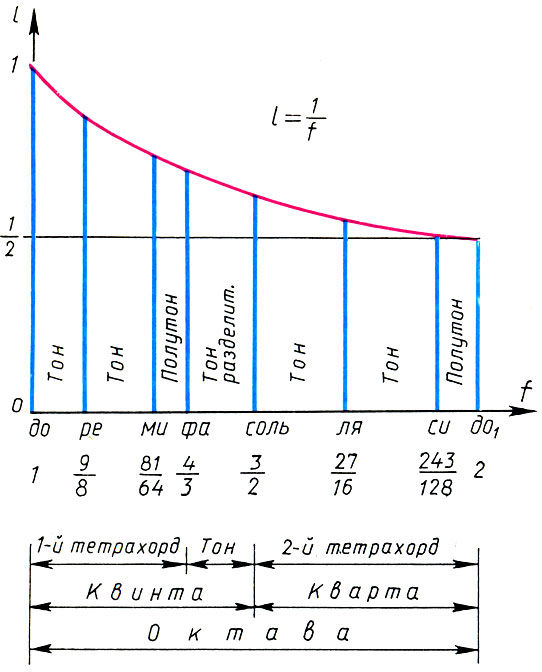
Pythagorean system of the Lydian scale and its mathematical characteristics
Knowing the size of the intervals that form, for example, the Lydian harmony and the rules of action with them, it is easy to obtain a mathematical expression of this range, that is, to build its Pythagorean system. Taking the frequency of the lower tone for the unit f 1 = 1, we find the first tetrachord: f 1 = 1, f 2 = 9/8, f 3 = 9/8 * 9/8 = 81/64, f 4 = 4/3. The second tetrachord is obtained by shifting the first by a fifth: f 5 = 3/2 f l = 3/2 , f 6 = 3/2 f 2 = 27/16 , f 7 = 3/2 f 3 = 243/128 , f 8 = 3/2 f 4 = 2. Finally for interval coefficients we have
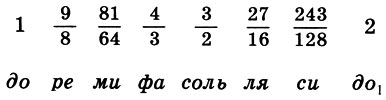 (6.14)
(6.14)This is the canon of Pythagoras. According to legend, the canon of Pythagoras first found practical application in tuning the lyre of the legendary Orpheus.
There was another way to arrange tetrachords in the octave. Ancient theorists “glued” tetrachords together so that the upper sound of one tetrachord was the lower sound of the second. Then the complementary to octave tone was placed at the bottom or at the top of such a system. If this tone was placed below, then the prefix Hypo- (under-) was added to the name of the tetrachord, and if above it was added the prefix Hyper- (above-). So it turned out 6 more harmonies, among which two pairs (hypo-Phrygian — Hyperlidian and Hypodorian — Hyper-Fri) are exactly the same. Rejecting the two extra scales, there were seven main modes. These frets were of great importance not only in ancient music, but after a thousand years they continued to live in medieval frets, and after two thousand years they lived in modern natural frets. True, medieval monks confused the names of their frets in comparison with the ancient ones, which often gives rise to various misunderstandings. Table 1 contains all the main antique frets, the order of the intervals in them is indicated, considering that the lower sound is located on the left and the upper sound is on the right, their ancient Greek and medieval names are given, and their inclination is indicated. Dividing tone is circled.
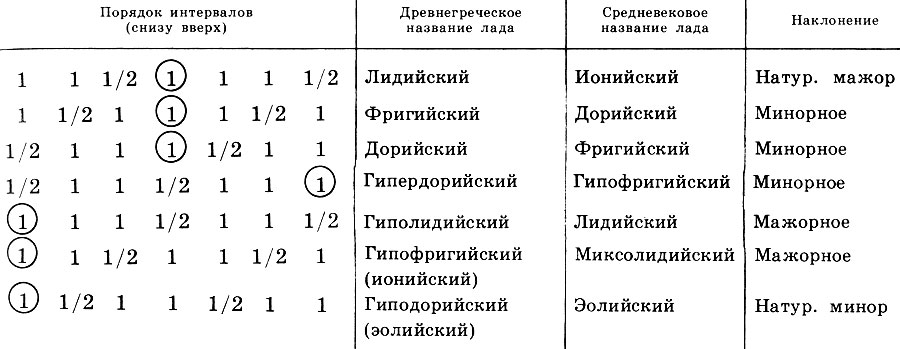
Table 1. The order of the intervals of tone (1) and semitone (1/2) in the antique mode (bottom to top), ancient Greek and medieval names of the frets and their inclinations
, — , , . - , «», . , .

. Relief
, «» , . , , ,- (. 551-479 . . .), : « , — ». , , , . , , , , . , , , . , . , , . , , «» , , , , .
«» , , , , . «» , , (), , ( — «» ), ( — ), (, ).
«» (. 124 — ?) «»: « - . , , , , , , , , ».
, ! ? , , , ! , , , . , . , « » . . (1893-1988) * : « — -. , , , . „“ , , , - — . — … , ».
* ( . , 95- — « ». , , (1927 — 1930), , , , - , : « , ». — « » — . - . . , . . . . )
? , , — ! , , , . , « » « ».
, , «» . , , , , , «». , , 10. (, , . .), , , — . « » , - , . (, , — — ), — — . , № 2 . 9 . , — — . « », . , , « ». -…
« » — () (l 2 /l 1 = 1, . . ), . , .
— . , — . « » . . (1900-1955). (« ...») (l 1 /l 2 = 2), . . (l 1 /l 2 = 3/2) , , .
(l 1 /l 2 = 4/3), «», « », «». , .
«» : , , . . , « » , , , .
(l 1 /l 2 = 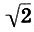 ). «» « »
). «» « » 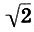 .
.
" " .
Source: https://habr.com/ru/post/416969/
All Articles