The Early Universe 1. Inflationary Cosmology: Is our universe part of the multiverse? Part 1
On the website of free lectures MIT OpenCourseWare posted a course of lectures on cosmology by Alan Gus, one of the creators of the inflationary model of the universe. The course seemed interesting enough to me to translate it.
Your attention is invited to the translation of the first lecture: “Inflationary Cosmology. Is our universe part of the multiverse? Part 1".

The title slide shows a photograph of the Planck satellite. This satellite was launched several years ago to measure cosmic background radiation. Cosmic background radiation is the most important key to understanding the history of the universe. Planck is the third satellite that is fully designed to measure cosmic background radiation. The first satellite was called COBE, then it was WMAP, now Planck.
Planck is still in orbit. In fact, he completed the data collection, although the analysis of this data is far from complete. We will also discuss what exactly this satellite is observing.
')

I want to begin by discussing the standard Big Bang theory, which will be the main theme of our course. We will spend about 2/3 of the course on the discussion of the standard Big Bang theory, and then move on to topics such as inflation. When we proceed to the study of inflation, it turns out that inflation is a fairly simple thing, if you understand the basic equations that arise in standard cosmology. It seems to me quite reasonable to spend two-thirds of the course on a standard cosmology before proceeding to inflation. By this time we will deal with all the principles that we will use later, studying advanced topics such as inflation.
The standard Big Bang model is the theory that the universe, such as we know it, appeared 13-14 billion years ago. Today we can even much more accurately call the age of the universe. The calculations are based on data from the Planck satellite, as well as some other information. Age is 13.82 ± 0.05 billion years. Thus, at present, the age of the universe since the Big Bang is pretty well established.
However, I knowingly specified "the universe as we know it." Because we are not completely sure that the universe began with what we call the Big Bang. We have a very good description of the Big Bang and we are quite sure that it really was, and we understand how it looked. But was there anything before him - this question is still completely open.
I think we should not assume that the universe began with the Big Bang. Later, at the very end of the course, when we study some of the effects of inflation and the multiverse, we will see that there are good reasons to believe that the Big Bang was not the beginning of the universe, but was only the beginning of our local universe, which is often called the pocket universe.
In any case, the Big Bang theory claims that at least our part of the universe 13.82 billion years ago was an extremely hot, dense, uniform particle substance that, according to the generally accepted standard model of the Big Bang, literally filled the entire space. Now we are confident enough that it uniformly filled all the space that is available for us to observe. I want to emphasize that this is contrary to the common, but incorrect visual picture of the Big Bang. According to this pictorial picture, the Big Bang looked like a small bomb of very dense matter, which then exploded and scattered in empty space. This is not a scientific picture of the Big Bang.
The reason is not the illogicality of such a picture. It is difficult to say what is logical here and what is illogical. It just contradicts what we see. If it were a small bomb that exploded in empty space, we would expect today that the universe looked differently, if you look in the direction where the bomb was, and in the opposite direction. But we see no signs of this. When we look at the sky, the universe with very great accuracy looks exactly the same in all directions. We do not see any signs of a bomb exploding anywhere. On the contrary, it seems that the Big Bang happened evenly everywhere.
The Big Bang describes several important things that we will talk about in more detail in our course. He describes how the early universe expanded and cooled, and we will spend quite some time to understand the nuances that lie behind these words. In fact, the Big Bang is a very accurate model based on very simple assumptions. By and large, we assume that the early universe was filled with hot gas, which was in thermodynamic equilibrium, and that this gas was expanding and contracting back due to gravity.
From these simple ideas we can calculate, and we will learn how to calculate how quickly the universe expanded, what temperature it had, the density of matter at each moment in time. All the nuances can be computed from these simple ideas, and it is really interesting to explore.
The Big Bang also explains how light chemical elements were formed. This is the main theme of Steve Weinberg’s book The First Three Minutes. Just about this period formed the chemical elements. It turns out that most of the chemical elements in the universe were formed not during the Big Bang, but much later inside the stars. These elements were scattered into space during supernova explosions, and stars from later generations were formed from them, one of which is our Sun.
Thus, the substance from which we are made, in fact, was not created during the Big Bang, but was synthesized inside some distant star, which had long ago exploded. Or maybe many stars whose remnants come together and formed our solar system. However, most of the substance in the universe, unlike most different kinds of elements, formed in the Big Bang. Most of the matter in the universe is just hydrogen and helium.
About five different isotopes of hydrogen, helium and lithium were mainly formed in the Big Bang, and since we have a detailed picture of the Big Bang, which we will study further, we can calculate and predict the number of these different isotopes. These predictions are in very good agreement with observations. This is undoubtedly one of the main proofs of the fact that our picture of the Big Bang is true. You can predict how much helium-3 should be. This quantity has been measured, and it is consistent with the predictions. It's amazing.
Finally, the Big Bang explains how the substance eventually gathered into clumps, and stars, galaxies, clusters of galaxies formed. We will talk about this a bit, but we will not dive very deeply into this topic, because it goes beyond our course. In principle, work in this direction is still ongoing. People do not understand everything about galaxies. But the general picture, that everything began with an almost homogeneous Universe, and then matter gathered in clumps that formed galaxies and other structures, is considered true. And from this very simple picture one can understand a lot about the universe.
Now I want to talk about what the usual Big Bang theory doesn’t talk about, the emergence of new ideas such as inflation.

First, the conventional big bang theory says nothing about what caused the expansion of the universe. In fact, this is only a theory of the consequences of the explosion. In the scientific version of the Big Bang in the emerging universe, everything expands, without explaining how this expansion began. This explanation is not part of the Big Bang theory. So the scientific version of the big bang theory is not really the bang theory. In fact, this is the theory of the consequences of the explosion.
In addition, in the same way, the usual Big Bang theory says nothing about where all the matter came from. The theory actually assumes that for every particle that we see in the Universe today, at the very beginning there was, if not the particle itself, then at least some kind of predecessor particle, without explaining where all these particles came from. In short, I want to say that the Big Bang theory says nothing about what exploded, why it exploded, or what happened before it exploded. In the theory of the Big Bang, there really is no explosion. It is a non-explosive theory, despite its name.

Inflation, it turns out, provides answers, very plausible answers, to many of these questions. Basically, this is what we'll talk about today in the time remaining. As I said, in terms of the course, we will approach this topic in about the last third of the course.
What is cosmic inflation? In essence, this is a minor modification, in terms of the overall picture, of the standard Big Bang theory. The best word to describe it is a word that I think was coined in Hollywood. Inflation is a prequel to the usual theory of the Big Bang. This is a brief description of what happened before, just before the Big Bang. Thus, inflation is indeed the explanation of the big bang explosion in the sense that it really gives the thrust theory that led the universe to this huge expansion process that we call the big bang.
Inflation does it in such a way that I think of it as a miracle. When I use the word "miracle", I use it in a scientific sense, just something so amazing that it deserves to be called a miracle, although it is part of the laws of physics. There are only a few features of the laws of physics that are crucial for inflation. I will talk about two of them, which I consider to be a miracle because when I was a student, no one spoke about them at all. They simply were not part of the physics that people noticed and talked about.
The miracle of physics about which I speak is something known from the time of Einstein’s general theory of relativity, that gravity is not always an attraction. Gravity can act as a repulsion. Einstein described this in 1916, in the form of what he called the cosmological constant. The initial motivation for modifying the equations of the general theory of relativity was that Einstein considered the universe static. He realized that ordinary gravity would cause a static universe to shrink. The universe cannot remain static. Therefore, he introduced this element, the cosmological constant, to compensate for the attraction of ordinary gravity and to be able to build a static model of the universe.
As you will soon find out, such a model is completely wrong. The universe looks completely different. But the fact that the general theory of relativity can include this gravitational repulsion, which is compatible with all the principles of the general theory of relativity is an important thing that Einstein himself discovered. Inflation uses this opportunity, allowing gravity to be a repulsive force that has led the universe into the expansion phase we call the Big Bang.
In fact, if we combine the general theory of relativity with some generally accepted ideas of elementary particle physics, there are clear signs, not quite a prediction, but rather clear signs that at very high energy densities there are states of matter that literally turn gravity upside down and attraction turns into repulsion. Speaking a little more precisely, then, as we will learn later, gravitational repulsion is created by negative pressure.
According to the general theory of relativity, it turns out that both pressure and energy density can create a gravitational field. In contrast to Newtonian physics, where only the mass density creates a gravitational field.
Positive pressure creates an attractive gravitational field. Positive pressure is a kind of normal pressure, and attracting gravity is a kind of normal gravity. Normal pressure creates normal gravity. But negative pressure is possible, and negative pressure creates repulsive gravity. This is the secret of what makes inflation possible.
Thus, inflation assumes that at least a small portion of the repulsive gravitational substance existed in the early universe. We do not know exactly when inflation occurred in the history of the universe, or in other words, we do not know exactly at what levels of energy it occurred. But a very plausible possibility of when inflation could have happened is when energy levels in the Universe were comparable to energy levels in theories of the Grand Unification.

Theories of the Great Unification, which we will talk about a little later, are theories that combine weak, strong and electromagnetic interactions into one single interaction. This combination occurs at a typical energy of about 10 16 GeV, where GeV is approximately mass or energy equivalent to the mass of a proton. We are talking about energies that are about 10 16 times greater than the equivalent energy of the mass of a proton. With such energies it is very possible that there will be states that create repulsive gravity.
If this happened with such orders of energy, the plot could initially be incredibly small - about 10 -28 centimeters in order to finally create all that we see at great distances. And the universe that we see today is entirely a consequence of such a site.
The gravitational repulsion created by this small area of repulsion gravitational matter became the driving force of the Big Bang, which led to the exponential expansion of the area. With exponential expansion, there is a certain time in which the size of the section doubles. If you wait the same amount again, it will double again. If you wait the same amount, he will double again.

Since these doublings quickly accumulate, it does not take much time to create the entire Universe. After about 100 doublings, this tiny stretch of 10 -28 centimeters in size may become large enough not to become a universe, but to become the size of a small ball, which will eventually become the observable universe, after it continues to expand after the end of inflation.
If all this happens on a grand unification theory, the doubling time is incredibly short, 10-37 seconds, which is very fast. The site is expanding exponentially, at least 10 28 times, which, as I have already mentioned, takes only about 100 doublings, and it can expand much more. There are no restrictions here. If it has expanded more than needed to create our universe, it simply means that the part of the universe in which we live is more than what we see. There is nothing wrong with that. Everything that we see looks uniform, and how far it extends we are not able to find out. Thus, the large size of inflation is fully consistent with what we see.
The time it takes is only 10 -35 seconds, which is 100 times in 10 -37 seconds. The site, which is destined to become our currently observable Universe, at the end of inflation becomes the size of a ball about a centimeter in diameter.
Inflation ends because this repulsive gravitational matter is unstable. It disintegrates, in the same sense as the radioactive substance decays. This does not mean that it is rotting like a decaying apple, it means that it turns into other kinds of matter. In particular, it turns into matter, which is no longer gravitationally repulsive. Thus, the gravitational repulsion ends, and the particles created by the energy released at the end of inflation become the hot substance of an ordinary Big Bang.
This ends the prequel, and the main action begins - the usual Big Bang theory. The role of inflation is only to create the initial conditions for the conventional theory of the Big Bang. There is a small nuance here. Inflation ends because matter is unstable, but ends almost everywhere, and not completely everywhere.
This repulsive gravitational matter decays, but it disintegrates as a radioactive substance, exponentially, it has a half-life. But no matter how long the half-lives pass, there will always be a tiny little piece, only a little bit of this matter will remain. And this turns out to be important for the idea that in many cases inflation never ends completely. We will come back to this.

Now I want to talk about what happens during the exponential expansion phase. There is a very specific feature of inflation, this caused by the repulsive gravity of exponential expansion, which is that while it occurs, the mass density or the energy density of this repulsive gravitational matter does not decrease. It would seem that if something doubles in size, then the volume should increase by 8 times, and the energy density should decrease by 8 times.
And this certainly happens with ordinary particles. So, of course, it would have happened if we had gas, ordinary gas, which we simply allowed to expand twice as much, the density would decrease eight times, because the volume is equal to the cube of size. But this particular repulsive gravitational matter actually expands with constant density. It sounds as if energy conservation is disturbed, because it means that the total amount of energy inside this expanding volume increases. The energy per unit volume remains constant, and the volume becomes more and more exponentially.
I contend that I have not lost my mind, that this actually corresponds to the laws of physics that we know. And that is consistent with the conservation of energy. Conservation of energy is indeed the sacred principle of physics.We do not know anything in nature that violates the principle of energy conservation. Energy ultimately cannot be created or destroyed, the total amount of energy is fixed. It seems there is a contradiction. How do we get rid of him?
This requires the second miracle of physics. Energy really is definitely conserved. The trick here is that energy is not necessarily positive. There are things that have negative energy. In particular, the gravitational field has negative energy. This statement, by the way, is true both in Newtonian physics and in the general theory of relativity. We will prove it later.
If you were on the course of electromagnetism, the calculation of the energy density of the electrostatic field, then you know that the energy density of the electrostatic field is proportional to the square of the electric field intensity. It can be proved that this energy is exactly equal to the energy that needs to be added to the system in order to create an electric field of a given configuration. If we compare Newton's law of gravity with Coulomb's law, it becomes clear that this is in fact the same law, except that they use different constants.
They are both inverse square laws and proportional to two charges, where in the case of gravity these are masses that play the role of charges. But they have opposite signs. Two positive charges, as is known, repel each other, two positive masses attract each other.
The same argument, which allows to calculate the energy density of the Coulomb field, allows us to calculate the energy density of the Newtonian gravitational field, still within the framework of Newtonian physics, while there remains a change in the sign of force. This changes the sign in all the calculations performed, and a negative value is obtained, which is the correct value for Newtonian gravity. The energy density of the Newtonian gravitational field is negative. The same is true in the general theory of relativity.
This means that within the framework of energy conservation, it is possible to obtain more and more matter, more and more energy accumulated as ordinary matter, which occurs during inflation, as long as there is a compensating amount of negative energy created by the gravitational field, which fills a larger area of space. This is exactly what happens during inflation.
The positive energy of this repulsive gravitational substance, which grows and grows in volume, is exactly compensated by the negative energy of the gravitational field that fills the plot. Thus, the total energy remains constant, as it should, and there is a high probability that the total energy is exactly zero. Because everything we know at least agrees with the possibility that these two energies are exactly equal to each other or very close.

Schematically, the picture is that the total energy of the Universe consists of a huge positive energy in the form of matter and radiation, the matter with which we see, the matter with which we usually identify energy. But there is also a huge negative energy contained in the gravitational field that fills the universe. And, as far as we can judge, their sum can be equal to 0. At least, this does not contradict anything.
In any case, during inflation, the black bar goes up, and the red bar goes down. And they rise and fall on an equal amount. Thus, the processes occurring during inflation, save energy, because everything that complies with the laws of physics, of which we know, must save energy.

I want to talk about some evidence of the existence of inflation. So far, I have described what inflation is, and today this description is sufficient. As I said, we will come back and talk about all this in our course. Now let's discuss some reasons why we believe that our Universe may have really undergone this process called inflation, which I just mentioned. There are three things I want to talk about.
The first is the uniformity of the universe on a large scale. This is due to what I told you at the beginning, that if you look in different directions, the Universe looks the same in all directions. An object whose dependence on direction can be measured with the greatest accuracy is the cosmic background radiation, because we can measure it in any direction, and it is extremely homogeneous.
When this was done, it was discovered that the cosmic background radiation is uniform with incredible accuracy - about 1/100000. This is an impressive level of uniformity. This means that the universe is really extremely homogeneous.
I want to make one reservation here to be completely accurate. If you just take and measure cosmic radiation, it turns out that there is an asymmetry that is larger than what I just said. Asymmetry can be found around 1/1000, where one direction is hotter than the opposite. But we interpret this one-thousandth effect as our movement through the cosmic background radiation, which makes it hotter in one direction and cold in the opposite direction. And this effect of our movement has a well-defined angular distribution.
We have no other way to find out what our speed is relative to the cosmic background radiation. We simply calculate it from this asymmetry. But we cannot explain everything with this movement. We can calculate the speed. As soon as we calculate it, it will determine one of the asymmetries that we can subtract. After that, residual asymmetries, asymmetries that we cannot explain, saying that the Earth has a certain speed with respect to cosmic background radiation, are at the level of one hundred thousandth. And this one hundred thousandth, we refer to the universe, and not to the motion of the Earth.
To understand the consequences of this incredible homogeneity, we need to say a little about the history of this cosmic background radiation. Radiation in the early period of the universe, when the universe was plasma, was essentially trapped in matter. The photons moved at the speed of light, but in plasma there is a very large cross section for the scattering of photons on free electrons. This means that the photons moved with the substance, because they could move freely only for a very short distance, then scatter and move in another direction. Thus, with respect to matter, the photons did not fly away during the first 400,000 years of the universe’s history.
But then, according to our calculations, after about 400,000 years, the universe cooled enough to neutralize the plasma. And when the plasma is neutralized, it becomes a neutral gas, like the air in this room. The air in this room seems to be completely transparent to us, and it turns out that this also happened in the universe.
The gas that filled the universe after its neutralization really became transparent. This means that the typical photon that we see today in cosmic background radiation traveled in a straight line from about 400,000 years after the Big Bang. Which, in turn, means that when we look at the cosmic background radiation, we, in fact, see an image of how the universe looked 400,000 years after the Big Bang. Just as the light coming from my face to your eyes gives you an idea of how I look.
So, we see an image of the universe at the age of 400,000 years, and it is uniform with an accuracy of one hundred thousandth. The question is, can we explain how the universe could become so homogeneous? If you are ready to simply assume that the universe was initially completely homogeneous for more than one thousandth, then no one bothers to do so. But if you want to try to explain this uniformity without assuming that it was from the very beginning, then with the help of the usual Big Bang theory it is simply impossible.
The reason is that within the framework of the evolutionary equations of the conventional theory of the Big Bang, it can be calculated, and we will calculate it later, in order to smooth everything over time, so that the cosmic background radiation looks smooth, you need to be able to move matter and energy about 100 times faster. the speed of light. Otherwise, it just won't work. We in physics do not know anything that happens faster than the speed of light. So, in the physics we know and in the usual theory of the Big Bang, there is no way to explain this homogeneity, except to simply assume that it was there from the very beginning. For reasons we don’t know.
On the other hand, inflation solves this problem very well. Inflation adds exponential expansion to the history of the universe. Due to the fact that this exponential expansion was so large that if you look at our universe before inflation occurred, it was much smaller than in conventional cosmology, in which it did not have this exponential expansion.
Thus, there was enough time in the inflationary model so that the observed part of the Universe became homogeneous before the start of inflation, when it was incredibly small. And it became homogeneous, like air, which spreads evenly throughout the room, rather than gathering in one corner. After homogeneity was achieved in this tiny region, inflation then stretched this region, which became large enough to include everything we see now, thus explaining why everything we see looks so uniform. This is a very simple explanation, and it is possible only with the use of inflation, and not within the framework of the generally accepted theory of the Big Bang.
In inflationary models, the Universe begins with such a small size that homogeneity is easily established. Just as the air in the lecture hall evenly fills the lecture hall. Then inflation stretches a region that is large enough to include everything that we are now seeing. This is the first of my three proofs of inflation.
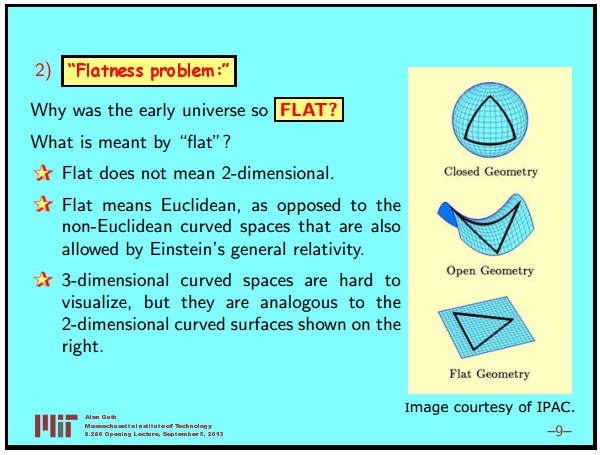
The second is what is called the problem of a flat universe. The question is, why was the early universe so flat? The question may immediately arise - what do I mean when I say that the early Universe was flat? One of the misconceptions that I sometimes encounter is that the flat is often perceived as two-dimensional. This is not what I mean. Flat does not mean like a two-dimensional pancake. The universe is three-dimensional. Flat in our case means Euclidean, obeys the axioms of Euclidean geometry, in contrast to the variants of non-Euclidean geometry, which are allowed by the general theory of relativity.
The general theory of relativity allows three-dimensional space to be curved. We consider only the uniform curvature. In reality, we see no curvature, but we know with greater accuracy that the universe is homogeneous than it is flat. So, imagine three possible curvature options for the universe, all of which will be considered homogeneous. Three-dimensional curved spaces are not easy to visualize, but all three of them are similar to two-dimensional curved spaces that are easier to imagine.
One of the options is the closed geometry of the surface of the sphere. The analogy is that a three-dimensional universe is analogous to a two-dimensional surface of a sphere. The number of measurements changes, but important things remain. So, for example, if you place a triangle on the surface of a sphere, and this can be easily visualized, the sum of its three angles will be more than 180 degrees. Unlike Euclidean geometry, where the sum is always 180 degrees.
STUDENT: Does the three-dimensional space bend in the fourth dimension? Just as two-dimensional models imply another dimension?
TEACHER: good question. The question was, does the three-dimensional curvature occur in the fourth dimension in the same way as the two-dimensional curvature occur in the third dimension? I think the answer is yes. But, I should clarify a little here. The third dimension from a purely mathematical point of view allows us to easily visualize the sphere. But from the point of view of people studying differential geometry, the geometry of a sphere is a clearly defined two-dimensional space without any need for a third dimension.
The third dimension is just a way for us to visualize the curvature. But the same method works for three-dimensional space. In fact, studying the three-dimensional curved space of a closed universe, we will do it that way. We use the same method, present it in four dimensions, and this will be very close to the two-dimensional picture you are looking at.
Thus, one of the possibilities is a closed geometry, where the sum of the three corners of the triangle is always more than 180 degrees. Another possibility is what is commonly called a saddle shape, or a space of negative curvature. In this case, the sum of the three corners, as they narrow, becomes less than 180 degrees. And only for a flat case, the sum of the three angles is exactly 180 degrees, which is the case of Euclidean geometry.
Geometry on the surfaces of these objects is not Euclidean, although if we consider the three-dimensional geometry of objects embedded in three-dimensional space, it is still Euclidean. But geometry on two-dimensional surfaces is not Euclidean on the top two surfaces, and Euclidean on the bottom surface.
This is how it works in the general theory of relativity. There are closed universes with a positive curvature and a sum of angles greater than 180 degrees. There are open universes where the sum of the three corners is always less than 180 degrees. And there is a case of a flat universe, which is on the border of these two, in which Euclidean geometry works. In our universe, Euclidean geometry works very well. That's why we all taught her at school. We have very good evidence that the early Universe was unusually close to this flat case of Euclidean geometry. This is what we are trying to understand and explain.
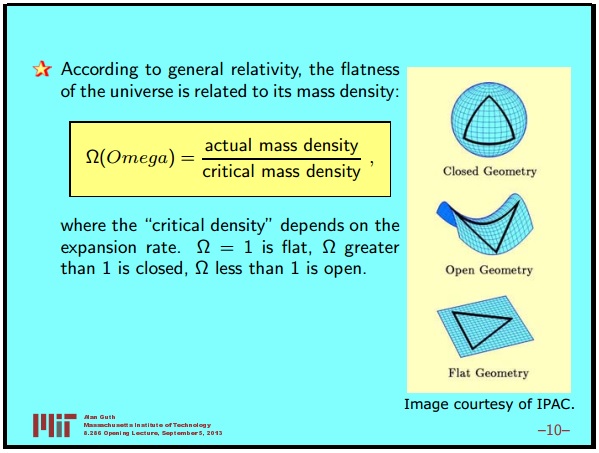
In accordance with the general theory of relativity, the geometry of the universe is determined by the density of mass. There is a certain value of the mass density, called the critical density, which depends on the rate of expansion, by the way, this is in no way a universal constant. But for a given expansion rate, you can calculate the critical density, and this critical density is the density that makes the universe flat. Cosmologists determine a number called Ω (Omega). Ω is simply the ratio of the actual mass density to the critical mass density. So, if Ω is 1, then the actual density is equal to the critical density, which means a flat universe. If Ω is greater than 1, then a closed universe will result, and if Ω is less than 1, the open Universe will be.
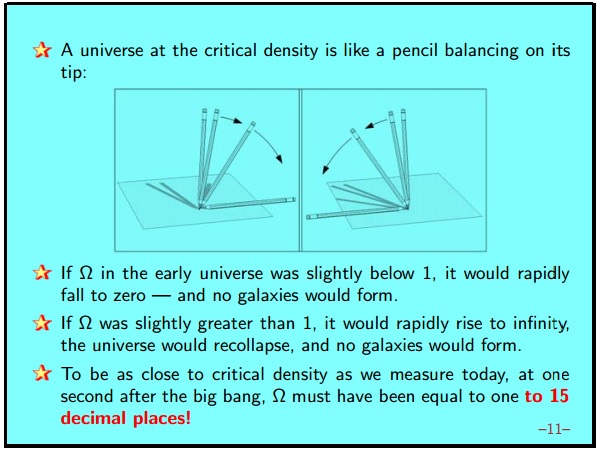
The evolution of the value of Ω is special because Ω is equal to 1, during the development of the Universe in ordinary cosmology, it behaves very much like a pencil balancing on its tip. This is an unstable equilibrium point. In other words, if Ω were exactly equal to 1 in the early Universe, it would remain exactly equal to 1. Just like a pencil, which is ideally placed on its tip, it will not know where to fall and in principle will remain in this position forever. At least in classical mechanics. We will not consider quantum mechanics for our pencil. For the analogy, we use a pencil of classical mechanics.
But if the pencil leans slightly in any direction, it will quickly begin to fall in that direction. Similarly, if Ω in the early universe were a little more than 1, it would quickly increase to infinity. This is a closed universe. Infinity in effect means that the universe reaches its maximum size, then begins to shrink and collapses. If Ω were a little less than 1, it would quickly decrease to 0, and the universe would simply become empty, as it would quickly expand.
Therefore, the only way for Ω to be close to 1 today, and as far as we can tell, Ω today is 1 - this is initially incredibly close to 1. It’s like that pencil that has stood for 14 billion years and hasn’t yet fallen. Numerically, in order for Ω to be somewhere in the allowable range very close to 1 today, it means that Ω one second after the Big Bang had to be equal to 1 with an incredible accuracy of 15 decimal places. This makes the density of the mass of the universe one second after the Big Bang, probably the most accurate number that we know in physics. We really know it to within 15 decimal places. If it were not in this range, then it would not be close to 1 today due to the amplification effect during the evolution of the universe.
The question is, how did this happen? In the usual Big Bang theory, theoretically, the initial value of Ω could be anything. To correspond to what we are seeing now, it should have been in this incredibly narrow range, but in theory there is nothing that would force him to be there. The question is, why was Ω originally so incredibly close to 1? As in the earlier mentioned problem of homogeneity, one can simply assume that it initially turned out to be what it should be, i.e. equal to 1. You can do so. But if you want to have some explanation of why this happened, there is nothing in ordinary cosmology that can explain it. However, inflation allows us to explain this.

In the inflationary model, the evolution of Ω changes, because gravity turns into a repulsive force instead of an attracting force, and this causes Ω to change differently. It turns out that during inflation, Ω does not move away from 1, as it did throughout the rest of the history of the universe, but, on the contrary, quickly moves to 1, exponentially fast. With this amount of inflation, which we talked about, inflation is about 10 28 times, it is enough that the value of Ω before inflation is not severely limited. Ω before inflation could not be 1, but could be 2 or 10 or 1/10 or 100 or 1/100.
The farther the initial Ω was from 1, the longer the inflation will be required to bring it sufficiently close to 1. But for Ω which is significantly different from 1, inflation will not take much longer, since inflation brings the omega to 1 exponentially. This is a very powerful force, bringing omega closer to 1. And this gives us a very simple explanation of why Ω in the early universe seemed to be extremely close to 1.
In fact, this prediction follows. Since inflation is so close to Ω to 1, we expect that today Ω really should be 1, or within the limits of the measured accuracy. You can imagine inflationary models, where Ω would turn out to be, say 0.2, this is what it was previously thought of, but to do this, inflation must end at exactly the right time before it gets even closer to 1. Because every exponential increase makes it even an order of magnitude closer to 1. This is a very fast effect. Therefore, without very careful adjustment, the majority of any inflationary models will bring Ω so close to 1 that today we see it as 1.
Previously, it seemed that it is not. Until 1998, astronomers were confident that Ω was only 0.2 or 0.3, while inflation had a fairly clear prediction that Ω should be 1. For me personally, this was quite a big inconvenience. Whenever I dined with astronomers, they said that inflation is a beautiful theory, but it cannot be correct, because Ω is 0.2, and inflation predicts Ω is 1. And this is just a discrepancy.
That all changed in 1998. Now the most accurate number for Ω that we have, obtained from the Planck satellite, along with some other measurements, is 1.0010, ± 0.0065. 0.0065 is an important thing. The number is very, very close to 1, and the margin of error is greater than this difference. Thus, today we know that with an accuracy of 0.5% or, maybe, 1%, Ω is equal to 1, which is predicted by inflation.
The new component that made all this possible, which changed the measured omega value from 0.2 to 1, is a new component of the energy balance of the Universe, the discovery of what we call dark energy. We learn a lot about dark energy during the course. The discovery in 1998 was that the expansion of the Universe does not slow down under the influence of gravity, as was expected before that time, but instead the expansion of the Universe is in fact accelerating.
This acceleration must be due to something. What causes this acceleration is called dark energy. Even though there are significant gaps in knowledge about dark energy, we can still calculate how much it should be in order to create the acceleration that we observe. And when all this is added together, we get a number that is much better consistent with inflation than the previous one.
STUDENT: Was the accelerating Universe unknown at that time a factor due to which it was incorrectly believed that Ω was 0.2 or 0.3?
TEACHER: Yes, it is. This was entirely due to the fact that it was not known about acceleration at that time. In fact, exactly measured the visible substance. This gave only 0.2 or 0.3. And this new component, the dark energy, which we know only because of acceleration, makes the necessary difference.
STUDENT: Is this data that makes Ω 0.2 or 0.3, really just a component of the Universe that we see through telescopes?
TEACHER: right. Including dark matter. In fact, we do not see everything. Without going into details now, we will discuss them later in the course; there is something called dark matter that is different from dark energy. Despite the fact that matter and energy are essentially the same, in our case they are different. Dark matter is matter, the conclusion about the existence of which we do because of its influence on another matter. Looking, for example, at the speed of rotation of galaxies, it is possible to calculate how much matter must be inside these galaxies for the orbits to be stable. It turns out that substances need much more than we actually see. This invisible matter is called dark matter, and it gives a contribution of 0.2 or 0.3. Visible matter is only about 0.04.
The next point I want to talk about is the heterogeneity of the universe on a small scale. On the largest scales, the universe is incredibly uniform - up to one thousandth, but on a smaller scale, the universe is extremely heterogeneous today. The Earth is a large cluster in the density distribution of the mass of the universe. Earth is about 10 30 degrees of times denser than the average density of matter in the universe. This is an incredibly tight clot. The question is, how did these clots form? Where did they come from?
We are confident that these bunches have evolved from the very minor disturbances that we see in the early universe, most clearly visible through cosmic background radiation. The mass density in the early universe, in our opinion, was homogeneous with an accuracy of about one hundred thousandth. But at the level of one hundred thousandth, we see that there are inhomogeneities in the cosmic background radiation.
Objects such as Earth have formed, because these small inhomogeneities in mass density are gravitationally unstable. In places where there is a slight excess of the density of a substance, this excess of density creates a gravitational field that attracts even more matter to these areas, which, in turn, produces an even stronger gravitational field that attracts even more matter. The system is unstable, it forms complex clusters that we see, such as galaxies, stars, planets, and so on.
This is a difficult process. But it all starts with these very weak discontinuities, which we believe existed shortly after the Big Bang. We see these inhomogeneities in the cosmic background radiation. Their measurement tells us a lot about the conditions in which the universe then existed and allows us to construct theories explaining how this universe came about. Satellites such as COBE, WMAP and Planck have been created to measure these inhomogeneities with very high accuracy.

Inflation answers the question of where the heterogeneity came from. In the usual Big Bang theory there was no explanation. It was simply assumed that the heterogeneities were there and they were added artificially, but there was no theory where they could come from. In inflationary models, where the whole substance is created by inflation, heterogeneities are also controlled by this inflation and appear due to quantum effects.
It is hard to believe that quantum effects can be important for the large-scale structure of the universe. The Andromeda Galaxy does not look as if it is a quantum oscillation. But if you look at this theory quantitatively, it really works very well. The theory is that the vibrations that we see in the cosmic background radiation were really purely a consequence of quantum theory, basically the uncertainty principle, which says that it is impossible to have something completely homogeneous. This is not consistent with the principle of uncertainty.
When we use the basic ideas of quantum mechanics, we can calculate the properties of these oscillations. To do this, we need to know more about very high energy physics, physics that was relevant in the period of inflation, in order to be able to predict the amplitude of these oscillations. We cannot predict amplitude. In principle, inflation would do this if we knew enough about the underlying particle physics, but we know too little about it. Therefore, in practice, we cannot predict amplitude.
However, inflationary models provide a very clear prediction of the spectrum of such fluctuations. By this I mean a change in the intensity of oscillations depending on the wavelength. Spectrum here means the same thing as for sound, except that you need to consider the wavelength, not the frequency, because these waves do not actually oscillate. But they have wavelengths just like sound waves, and, if we talk about the intensity of different wavelengths, the idea of the spectrum is really the same as in sound.

It can be measured. These are not exactly the last measurements, these are the last measurements for which I have a schedule. The red line is a theoretical prediction. Black dots are real measurements. This is a seven-year WMAP data. It is difficult to convey how happy I was when I saw this curve.
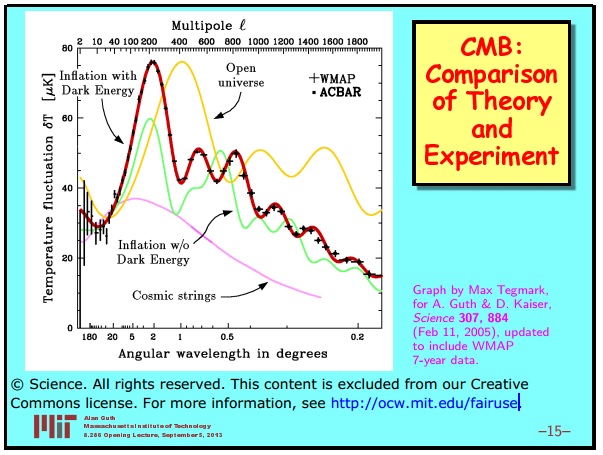
I also have graphs of what other theories predict. For a while, for example, people took very seriously the idea that the heterogeneities that we see in the Universe, these fluctuations, may have been caused by the random formation of so-called cosmic strings, which were formed in phase transitions in the early Universe. It was certainly a viable idea at one time, but as soon as this curve was measured, it turned out that the prediction of cosmic strings did not look like it at all. Since then, they have been excluded as a source of density fluctuations in the universe. Various other models are also shown here. I will not waste time on them, because there are other things that I want to talk about.

In any case, this is undoubted success. And this is the latest data. This is data from the Planck satellite, which was launched last March. I do not have it on the graph at the same scale, but again you see a theoretical curve based on inflation and points that show data with small tiny lines of errors. Absolutely clear match.
STUDENT: what happened to the theory of inflation after dark energy was discovered? Has it changed significantly?
TEACHER: Has the theory changed?
STUDENT: on the previous graph there was a different curve.
TEACHER: for inflation without dark energy. I think that not so much the theory of inflation is different for these two curves, but the curve that you see today is the result of inflation and the evolution that has occurred since then. And it is the evolution that has happened since then that makes a big difference between these curves.
Thus, the theory of inflation should not have changed much. And she really did not change. But, of course, the curve looks much better after dark energy was discovered, because the correct mass density became known, and gradually we got more and more data about these fluctuations that fit perfectly into what inflation predicts.

Now I want to go to the idea of the multiverse. I will try to quickly run through it so that we can finish. We still will not try to understand all the details now, so I will tell you about some of them in the remaining 10 minutes of the lecture. I want to talk a little bit about how inflation leads to the idea of the multiverse. We will come back to this at the very end of the course, and this is certainly a fascinating aspect of inflation.
Gravitationally repulsive material that creates inflation is metastable, as we said. He breaks up. This means that if you are in a place where inflation occurs, and ask yourself what the probability is that it will happen a little later, this probability decreases exponentially — it decreases twice in each doubling, each half-life. But at the same time, the volume of any area that swells up also grows exponentially, growing due to inflation. In fact, in any reasonable inflationary model, growth rates are much faster than rates of decay. If you look at the area that swells, if you wait for the half-life, half the volume of this area will no longer swell, by definition, the half-life. But the remaining half will be much larger than the volume with which we started. That's the whole point.
This is a very unusual situation, because it seems to have no end. The area that swells becomes more and more, even when it disintegrates, because expansion is faster than decay. This leads to the phenomenon of eternal inflation. The size of the swelling area increases with time, despite the fact that the swelling matter disintegrates. This leads to what we call eternal inflation. Eternal here means eternal in the future, as far as we can judge, but not eternal in the past. Inflation begins at some finite time, but then, as soon as it starts, it will continue forever.
Whenever a part of this swelling region goes through a phase transition and becomes normal, it locally looks like a Big Bang. Our Big Bang is one of these local events, and the universe formed by any of these local events where the expanding region disintegrates is called the pocket universe. Pocket simply because there are many such universes on the scale of this multiverse. They are in some sense small, although they are the same size as the universe in which we live. And our universe is one of those pocket universes.
Thus, instead of a single universe, inflation produces an infinite number of them. This is what we call the multiverse. It is worth noting that the word multiverse is also used in other contexts and other theories, but inflation, I think, is the most plausible way to build a multiverse. This is what most cosmologists have in mind when they talk about the multiverse.

What is the place of dark energy here? She plays a very important role. In 1998, two groups of astronomers, independently of each other, discovered that the universe is now expanding with acceleration. We now know that the universe has expanded rapidly over the past five billion years out of 14 billion years of universe history. There was a period when expansion slowed down to five billion years ago. The consequence of this is that inflation actually happens today. This accelerated expansion of the universe, which we see, is very similar to inflation, and we really interpret it as a similar kind of physics. We believe that it is caused by some kind of negative pressure, just as inflation was caused by negative pressure.
This matter, which apparently fills space and has negative pressure, we call dark energy. Dark energy is simply by definition something, whatever it is that causes this acceleration. One may ask, what is dark energy really about? The surest answer to this is nobody knows. However, there is the most plausible candidate. The most likely candidate, and other candidates are not very different from him, simply lies in the fact that dark energy is the energy of a vacuum. The energy of emptiness. It may be surprising that emptiness can have energy. But I will tell about it, and it is not so surprising.
But if dark energy is just vacuum energy, it fully corresponds to everything we know about the nature of the expansion of the universe, what we can measure.
STUDENT: why only in the last five billion years has the universe begun to expand rapidly?
TEACHER: I can now explain this. Now that I have said that there is probably vacuum energy, I can give you the answer. The answer is that the vacuum energy does not change with time, because it is just the vacuum energy. This is the same as I said about the energy density during inflation. This is just a constant. At the same time, ordinary matter becomes more discharged as the universe expands, reducing its density in proportion to the cube of the size of the universe.
It so happened that earlier about the last five billion years, ordinary matter dominated the universe, which created attracting gravity and caused the universe to slow down. But then, about five billion years ago, matter in the universe became so discharged that ordinary matter ceased to dominate the vacuum energy, and the vacuum energy began to cause acceleration. Vacuum energy was all the time, causing repulsion, but it was dominated by attracting gravity of ordinary matter until the last five billion years.

Now I want to talk, why can something be in the void? Why can emptiness have energy? The answer is actually quite clear to physicists today. Quantum vacuum, in contrast to the classical vacuum, is a very complex state. It is not at all empty. This is actually a complex set of vacuum oscillations. We think that even there is a field called the Higgs field, which you probably heard about, which on average has a non-zero value in a vacuum. Things like an electromagnetic field constantly oscillate in a vacuum due to the uncertainty principle, which leads to the presence of energy density in these fluctuations.
So, as far as we can judge, there is no reason for the vacuum energy to be zero. But this does not mean that we understand what its value is. Today, the real problem from the point of view of fundamental physics is not finding out why a vacuum can have a non-zero energy density. The problem is to understand why she is so small. Why is this a problem? Quantum field theory, which we will not study in detail, says that, for example, the electromagnetic field constantly fluctuates. This is due to the principle of uncertainty. These vibrations can have any wavelength. And each wavelength contributes to the energy density of the vacuum fluctuations.
There is no shortest wavelength. In a box of any size, there is the longest wavelength, but not the shortest wavelength. It turns out that when we try to calculate the vacuum energy density in quantum field theory, it diverges from the side of short wavelengths. It becomes literally infinite, since the formal calculation shows that all wavelengths contribute, and the shortest wavelength does not exist.
What does this mean in real physics? We believe that this is not necessarily a problem with our understanding of quantum field theory. In fact, we believe that this is only a limitation of the range in which our assumptions are correct. Of course, quantum theory works extremely well when it is tested in the laboratory. We think that at very short wavelengths something should limit this infinity. A good candidate for limiting infinity at short wavelengths is quantum gravity effects, which we do not understand.
Thus, one of the ways to estimate the true energy density predicted by quantum field theory is to limit the wavelength on the Planck scale, the energy scale, the length scale associated with quantum gravity, which is about 10 -33 centimeters. If you do this, then you can calculate the energy density of the electromagnetic field of a vacuum and get a finite number. But it is too big. It differs not by some small number, but very much. It is more by 120 orders of magnitude. Thus, we do not understand why the vacuum energy is as it is, since our simple estimates say that it should be 120 orders of magnitude larger.
It must be said that there is still a way out. The energy that we calculated here is only one of the contributions to the total vacuum energy. There are also negative contributions. If we calculate the fluctuation of the electron field, then its contribution to the energy will be negative. In principle, it is possible that these contributions accurately or almost exactly compensate each other, but we do not know why they should do this. Thus, there is a big question about the theoretical prediction of the vacuum energy density.

Now I want to tell a little about the landscape of string theory, which may be a possible explanation for the smallness of the vacuum energy. This is only a possible explanation, everything is very speculative here. But one possible explanation for this very small vacuum energy, which we observe, combines the idea of perpetual inflation and string theory. It is based on the idea that string theory does not have a unique vacuum. For many years, theorists have unsuccessfully tried to find a vacuum in string theory. They simply could not understand how the vacuum theory should look like in string theory.
And then, a little more than 10 years ago, many string theorists began to unite around the idea that maybe they could not find a vacuum, because there is no unique vacuum for string theory. Instead, they now claim that there are a huge number, they view numbers like 10,500 , an enormous number of metastable states that live long, any of which may look like a vacuum for a long period of time, even if it may eventually decay or go to one of the other metastable states. This is called string theory landscape. This huge set of vacuum states, any of which can be a vacuum, which, for example, fills in some pocket universe.
If we combine this with the idea of eternal inflation, then we can conclude that during the eternal inflation, all these 10,500 or more kinds of vacuum are likely to arise. That is, different pocket universes within themselves will have different types of vacuum, created randomly. Then we will have a multiverse, which will consist of many, up to 10,500 degrees or more different types of vacuums in different pocket universes.
With this assumption, string theory is the supposed law of physics that governs everything. But if you lived in one of these pocket universes, you would actually see the laws of physics, which were very different from the laws in other pocket universes. The fact is that the physics we actually see and measure is low energy physics compared to the energy scale of string theory. We see only small fluctuations in the structure of the vacuum in which we live.
So the particles that we see - electrons and quarks, which are combined into protons and neutrons, can be characteristic of our particular pocket universe. In other pocket universes there may be completely different kinds of particles that are oscillations of other kinds of vacuum. So, even if the laws of physics are the same everywhere - the laws of string theory, in practice, the observed laws of physics can vary greatly from one pocket universe to another. In particular, due to the fact that there is a different vacuum in different universes, the vacuum energy density may be different in different universes. And this gives a possible answer to why the observed vacuum energy is so small.
We will talk about this next time.
Your attention is invited to the translation of the first lecture: “Inflationary Cosmology. Is our universe part of the multiverse? Part 1".

The title slide shows a photograph of the Planck satellite. This satellite was launched several years ago to measure cosmic background radiation. Cosmic background radiation is the most important key to understanding the history of the universe. Planck is the third satellite that is fully designed to measure cosmic background radiation. The first satellite was called COBE, then it was WMAP, now Planck.
Planck is still in orbit. In fact, he completed the data collection, although the analysis of this data is far from complete. We will also discuss what exactly this satellite is observing.
')

I want to begin by discussing the standard Big Bang theory, which will be the main theme of our course. We will spend about 2/3 of the course on the discussion of the standard Big Bang theory, and then move on to topics such as inflation. When we proceed to the study of inflation, it turns out that inflation is a fairly simple thing, if you understand the basic equations that arise in standard cosmology. It seems to me quite reasonable to spend two-thirds of the course on a standard cosmology before proceeding to inflation. By this time we will deal with all the principles that we will use later, studying advanced topics such as inflation.
The standard Big Bang model is the theory that the universe, such as we know it, appeared 13-14 billion years ago. Today we can even much more accurately call the age of the universe. The calculations are based on data from the Planck satellite, as well as some other information. Age is 13.82 ± 0.05 billion years. Thus, at present, the age of the universe since the Big Bang is pretty well established.
However, I knowingly specified "the universe as we know it." Because we are not completely sure that the universe began with what we call the Big Bang. We have a very good description of the Big Bang and we are quite sure that it really was, and we understand how it looked. But was there anything before him - this question is still completely open.
I think we should not assume that the universe began with the Big Bang. Later, at the very end of the course, when we study some of the effects of inflation and the multiverse, we will see that there are good reasons to believe that the Big Bang was not the beginning of the universe, but was only the beginning of our local universe, which is often called the pocket universe.
In any case, the Big Bang theory claims that at least our part of the universe 13.82 billion years ago was an extremely hot, dense, uniform particle substance that, according to the generally accepted standard model of the Big Bang, literally filled the entire space. Now we are confident enough that it uniformly filled all the space that is available for us to observe. I want to emphasize that this is contrary to the common, but incorrect visual picture of the Big Bang. According to this pictorial picture, the Big Bang looked like a small bomb of very dense matter, which then exploded and scattered in empty space. This is not a scientific picture of the Big Bang.
The reason is not the illogicality of such a picture. It is difficult to say what is logical here and what is illogical. It just contradicts what we see. If it were a small bomb that exploded in empty space, we would expect today that the universe looked differently, if you look in the direction where the bomb was, and in the opposite direction. But we see no signs of this. When we look at the sky, the universe with very great accuracy looks exactly the same in all directions. We do not see any signs of a bomb exploding anywhere. On the contrary, it seems that the Big Bang happened evenly everywhere.
The Big Bang describes several important things that we will talk about in more detail in our course. He describes how the early universe expanded and cooled, and we will spend quite some time to understand the nuances that lie behind these words. In fact, the Big Bang is a very accurate model based on very simple assumptions. By and large, we assume that the early universe was filled with hot gas, which was in thermodynamic equilibrium, and that this gas was expanding and contracting back due to gravity.
From these simple ideas we can calculate, and we will learn how to calculate how quickly the universe expanded, what temperature it had, the density of matter at each moment in time. All the nuances can be computed from these simple ideas, and it is really interesting to explore.
The Big Bang also explains how light chemical elements were formed. This is the main theme of Steve Weinberg’s book The First Three Minutes. Just about this period formed the chemical elements. It turns out that most of the chemical elements in the universe were formed not during the Big Bang, but much later inside the stars. These elements were scattered into space during supernova explosions, and stars from later generations were formed from them, one of which is our Sun.
Thus, the substance from which we are made, in fact, was not created during the Big Bang, but was synthesized inside some distant star, which had long ago exploded. Or maybe many stars whose remnants come together and formed our solar system. However, most of the substance in the universe, unlike most different kinds of elements, formed in the Big Bang. Most of the matter in the universe is just hydrogen and helium.
About five different isotopes of hydrogen, helium and lithium were mainly formed in the Big Bang, and since we have a detailed picture of the Big Bang, which we will study further, we can calculate and predict the number of these different isotopes. These predictions are in very good agreement with observations. This is undoubtedly one of the main proofs of the fact that our picture of the Big Bang is true. You can predict how much helium-3 should be. This quantity has been measured, and it is consistent with the predictions. It's amazing.
Finally, the Big Bang explains how the substance eventually gathered into clumps, and stars, galaxies, clusters of galaxies formed. We will talk about this a bit, but we will not dive very deeply into this topic, because it goes beyond our course. In principle, work in this direction is still ongoing. People do not understand everything about galaxies. But the general picture, that everything began with an almost homogeneous Universe, and then matter gathered in clumps that formed galaxies and other structures, is considered true. And from this very simple picture one can understand a lot about the universe.
Now I want to talk about what the usual Big Bang theory doesn’t talk about, the emergence of new ideas such as inflation.

First, the conventional big bang theory says nothing about what caused the expansion of the universe. In fact, this is only a theory of the consequences of the explosion. In the scientific version of the Big Bang in the emerging universe, everything expands, without explaining how this expansion began. This explanation is not part of the Big Bang theory. So the scientific version of the big bang theory is not really the bang theory. In fact, this is the theory of the consequences of the explosion.
In addition, in the same way, the usual Big Bang theory says nothing about where all the matter came from. The theory actually assumes that for every particle that we see in the Universe today, at the very beginning there was, if not the particle itself, then at least some kind of predecessor particle, without explaining where all these particles came from. In short, I want to say that the Big Bang theory says nothing about what exploded, why it exploded, or what happened before it exploded. In the theory of the Big Bang, there really is no explosion. It is a non-explosive theory, despite its name.

Inflation, it turns out, provides answers, very plausible answers, to many of these questions. Basically, this is what we'll talk about today in the time remaining. As I said, in terms of the course, we will approach this topic in about the last third of the course.
What is cosmic inflation? In essence, this is a minor modification, in terms of the overall picture, of the standard Big Bang theory. The best word to describe it is a word that I think was coined in Hollywood. Inflation is a prequel to the usual theory of the Big Bang. This is a brief description of what happened before, just before the Big Bang. Thus, inflation is indeed the explanation of the big bang explosion in the sense that it really gives the thrust theory that led the universe to this huge expansion process that we call the big bang.
Inflation does it in such a way that I think of it as a miracle. When I use the word "miracle", I use it in a scientific sense, just something so amazing that it deserves to be called a miracle, although it is part of the laws of physics. There are only a few features of the laws of physics that are crucial for inflation. I will talk about two of them, which I consider to be a miracle because when I was a student, no one spoke about them at all. They simply were not part of the physics that people noticed and talked about.
The miracle of physics about which I speak is something known from the time of Einstein’s general theory of relativity, that gravity is not always an attraction. Gravity can act as a repulsion. Einstein described this in 1916, in the form of what he called the cosmological constant. The initial motivation for modifying the equations of the general theory of relativity was that Einstein considered the universe static. He realized that ordinary gravity would cause a static universe to shrink. The universe cannot remain static. Therefore, he introduced this element, the cosmological constant, to compensate for the attraction of ordinary gravity and to be able to build a static model of the universe.
As you will soon find out, such a model is completely wrong. The universe looks completely different. But the fact that the general theory of relativity can include this gravitational repulsion, which is compatible with all the principles of the general theory of relativity is an important thing that Einstein himself discovered. Inflation uses this opportunity, allowing gravity to be a repulsive force that has led the universe into the expansion phase we call the Big Bang.
In fact, if we combine the general theory of relativity with some generally accepted ideas of elementary particle physics, there are clear signs, not quite a prediction, but rather clear signs that at very high energy densities there are states of matter that literally turn gravity upside down and attraction turns into repulsion. Speaking a little more precisely, then, as we will learn later, gravitational repulsion is created by negative pressure.
According to the general theory of relativity, it turns out that both pressure and energy density can create a gravitational field. In contrast to Newtonian physics, where only the mass density creates a gravitational field.
Positive pressure creates an attractive gravitational field. Positive pressure is a kind of normal pressure, and attracting gravity is a kind of normal gravity. Normal pressure creates normal gravity. But negative pressure is possible, and negative pressure creates repulsive gravity. This is the secret of what makes inflation possible.
Thus, inflation assumes that at least a small portion of the repulsive gravitational substance existed in the early universe. We do not know exactly when inflation occurred in the history of the universe, or in other words, we do not know exactly at what levels of energy it occurred. But a very plausible possibility of when inflation could have happened is when energy levels in the Universe were comparable to energy levels in theories of the Grand Unification.

Theories of the Great Unification, which we will talk about a little later, are theories that combine weak, strong and electromagnetic interactions into one single interaction. This combination occurs at a typical energy of about 10 16 GeV, where GeV is approximately mass or energy equivalent to the mass of a proton. We are talking about energies that are about 10 16 times greater than the equivalent energy of the mass of a proton. With such energies it is very possible that there will be states that create repulsive gravity.
If this happened with such orders of energy, the plot could initially be incredibly small - about 10 -28 centimeters in order to finally create all that we see at great distances. And the universe that we see today is entirely a consequence of such a site.
The gravitational repulsion created by this small area of repulsion gravitational matter became the driving force of the Big Bang, which led to the exponential expansion of the area. With exponential expansion, there is a certain time in which the size of the section doubles. If you wait the same amount again, it will double again. If you wait the same amount, he will double again.

Since these doublings quickly accumulate, it does not take much time to create the entire Universe. After about 100 doublings, this tiny stretch of 10 -28 centimeters in size may become large enough not to become a universe, but to become the size of a small ball, which will eventually become the observable universe, after it continues to expand after the end of inflation.
If all this happens on a grand unification theory, the doubling time is incredibly short, 10-37 seconds, which is very fast. The site is expanding exponentially, at least 10 28 times, which, as I have already mentioned, takes only about 100 doublings, and it can expand much more. There are no restrictions here. If it has expanded more than needed to create our universe, it simply means that the part of the universe in which we live is more than what we see. There is nothing wrong with that. Everything that we see looks uniform, and how far it extends we are not able to find out. Thus, the large size of inflation is fully consistent with what we see.
The time it takes is only 10 -35 seconds, which is 100 times in 10 -37 seconds. The site, which is destined to become our currently observable Universe, at the end of inflation becomes the size of a ball about a centimeter in diameter.
Inflation ends because this repulsive gravitational matter is unstable. It disintegrates, in the same sense as the radioactive substance decays. This does not mean that it is rotting like a decaying apple, it means that it turns into other kinds of matter. In particular, it turns into matter, which is no longer gravitationally repulsive. Thus, the gravitational repulsion ends, and the particles created by the energy released at the end of inflation become the hot substance of an ordinary Big Bang.
This ends the prequel, and the main action begins - the usual Big Bang theory. The role of inflation is only to create the initial conditions for the conventional theory of the Big Bang. There is a small nuance here. Inflation ends because matter is unstable, but ends almost everywhere, and not completely everywhere.
This repulsive gravitational matter decays, but it disintegrates as a radioactive substance, exponentially, it has a half-life. But no matter how long the half-lives pass, there will always be a tiny little piece, only a little bit of this matter will remain. And this turns out to be important for the idea that in many cases inflation never ends completely. We will come back to this.

Now I want to talk about what happens during the exponential expansion phase. There is a very specific feature of inflation, this caused by the repulsive gravity of exponential expansion, which is that while it occurs, the mass density or the energy density of this repulsive gravitational matter does not decrease. It would seem that if something doubles in size, then the volume should increase by 8 times, and the energy density should decrease by 8 times.
And this certainly happens with ordinary particles. So, of course, it would have happened if we had gas, ordinary gas, which we simply allowed to expand twice as much, the density would decrease eight times, because the volume is equal to the cube of size. But this particular repulsive gravitational matter actually expands with constant density. It sounds as if energy conservation is disturbed, because it means that the total amount of energy inside this expanding volume increases. The energy per unit volume remains constant, and the volume becomes more and more exponentially.
I contend that I have not lost my mind, that this actually corresponds to the laws of physics that we know. And that is consistent with the conservation of energy. Conservation of energy is indeed the sacred principle of physics.We do not know anything in nature that violates the principle of energy conservation. Energy ultimately cannot be created or destroyed, the total amount of energy is fixed. It seems there is a contradiction. How do we get rid of him?
This requires the second miracle of physics. Energy really is definitely conserved. The trick here is that energy is not necessarily positive. There are things that have negative energy. In particular, the gravitational field has negative energy. This statement, by the way, is true both in Newtonian physics and in the general theory of relativity. We will prove it later.
If you were on the course of electromagnetism, the calculation of the energy density of the electrostatic field, then you know that the energy density of the electrostatic field is proportional to the square of the electric field intensity. It can be proved that this energy is exactly equal to the energy that needs to be added to the system in order to create an electric field of a given configuration. If we compare Newton's law of gravity with Coulomb's law, it becomes clear that this is in fact the same law, except that they use different constants.
They are both inverse square laws and proportional to two charges, where in the case of gravity these are masses that play the role of charges. But they have opposite signs. Two positive charges, as is known, repel each other, two positive masses attract each other.
The same argument, which allows to calculate the energy density of the Coulomb field, allows us to calculate the energy density of the Newtonian gravitational field, still within the framework of Newtonian physics, while there remains a change in the sign of force. This changes the sign in all the calculations performed, and a negative value is obtained, which is the correct value for Newtonian gravity. The energy density of the Newtonian gravitational field is negative. The same is true in the general theory of relativity.
This means that within the framework of energy conservation, it is possible to obtain more and more matter, more and more energy accumulated as ordinary matter, which occurs during inflation, as long as there is a compensating amount of negative energy created by the gravitational field, which fills a larger area of space. This is exactly what happens during inflation.
The positive energy of this repulsive gravitational substance, which grows and grows in volume, is exactly compensated by the negative energy of the gravitational field that fills the plot. Thus, the total energy remains constant, as it should, and there is a high probability that the total energy is exactly zero. Because everything we know at least agrees with the possibility that these two energies are exactly equal to each other or very close.

Schematically, the picture is that the total energy of the Universe consists of a huge positive energy in the form of matter and radiation, the matter with which we see, the matter with which we usually identify energy. But there is also a huge negative energy contained in the gravitational field that fills the universe. And, as far as we can judge, their sum can be equal to 0. At least, this does not contradict anything.
In any case, during inflation, the black bar goes up, and the red bar goes down. And they rise and fall on an equal amount. Thus, the processes occurring during inflation, save energy, because everything that complies with the laws of physics, of which we know, must save energy.

I want to talk about some evidence of the existence of inflation. So far, I have described what inflation is, and today this description is sufficient. As I said, we will come back and talk about all this in our course. Now let's discuss some reasons why we believe that our Universe may have really undergone this process called inflation, which I just mentioned. There are three things I want to talk about.
The first is the uniformity of the universe on a large scale. This is due to what I told you at the beginning, that if you look in different directions, the Universe looks the same in all directions. An object whose dependence on direction can be measured with the greatest accuracy is the cosmic background radiation, because we can measure it in any direction, and it is extremely homogeneous.
When this was done, it was discovered that the cosmic background radiation is uniform with incredible accuracy - about 1/100000. This is an impressive level of uniformity. This means that the universe is really extremely homogeneous.
I want to make one reservation here to be completely accurate. If you just take and measure cosmic radiation, it turns out that there is an asymmetry that is larger than what I just said. Asymmetry can be found around 1/1000, where one direction is hotter than the opposite. But we interpret this one-thousandth effect as our movement through the cosmic background radiation, which makes it hotter in one direction and cold in the opposite direction. And this effect of our movement has a well-defined angular distribution.
We have no other way to find out what our speed is relative to the cosmic background radiation. We simply calculate it from this asymmetry. But we cannot explain everything with this movement. We can calculate the speed. As soon as we calculate it, it will determine one of the asymmetries that we can subtract. After that, residual asymmetries, asymmetries that we cannot explain, saying that the Earth has a certain speed with respect to cosmic background radiation, are at the level of one hundred thousandth. And this one hundred thousandth, we refer to the universe, and not to the motion of the Earth.
To understand the consequences of this incredible homogeneity, we need to say a little about the history of this cosmic background radiation. Radiation in the early period of the universe, when the universe was plasma, was essentially trapped in matter. The photons moved at the speed of light, but in plasma there is a very large cross section for the scattering of photons on free electrons. This means that the photons moved with the substance, because they could move freely only for a very short distance, then scatter and move in another direction. Thus, with respect to matter, the photons did not fly away during the first 400,000 years of the universe’s history.
But then, according to our calculations, after about 400,000 years, the universe cooled enough to neutralize the plasma. And when the plasma is neutralized, it becomes a neutral gas, like the air in this room. The air in this room seems to be completely transparent to us, and it turns out that this also happened in the universe.
The gas that filled the universe after its neutralization really became transparent. This means that the typical photon that we see today in cosmic background radiation traveled in a straight line from about 400,000 years after the Big Bang. Which, in turn, means that when we look at the cosmic background radiation, we, in fact, see an image of how the universe looked 400,000 years after the Big Bang. Just as the light coming from my face to your eyes gives you an idea of how I look.
So, we see an image of the universe at the age of 400,000 years, and it is uniform with an accuracy of one hundred thousandth. The question is, can we explain how the universe could become so homogeneous? If you are ready to simply assume that the universe was initially completely homogeneous for more than one thousandth, then no one bothers to do so. But if you want to try to explain this uniformity without assuming that it was from the very beginning, then with the help of the usual Big Bang theory it is simply impossible.
The reason is that within the framework of the evolutionary equations of the conventional theory of the Big Bang, it can be calculated, and we will calculate it later, in order to smooth everything over time, so that the cosmic background radiation looks smooth, you need to be able to move matter and energy about 100 times faster. the speed of light. Otherwise, it just won't work. We in physics do not know anything that happens faster than the speed of light. So, in the physics we know and in the usual theory of the Big Bang, there is no way to explain this homogeneity, except to simply assume that it was there from the very beginning. For reasons we don’t know.
On the other hand, inflation solves this problem very well. Inflation adds exponential expansion to the history of the universe. Due to the fact that this exponential expansion was so large that if you look at our universe before inflation occurred, it was much smaller than in conventional cosmology, in which it did not have this exponential expansion.
Thus, there was enough time in the inflationary model so that the observed part of the Universe became homogeneous before the start of inflation, when it was incredibly small. And it became homogeneous, like air, which spreads evenly throughout the room, rather than gathering in one corner. After homogeneity was achieved in this tiny region, inflation then stretched this region, which became large enough to include everything we see now, thus explaining why everything we see looks so uniform. This is a very simple explanation, and it is possible only with the use of inflation, and not within the framework of the generally accepted theory of the Big Bang.
In inflationary models, the Universe begins with such a small size that homogeneity is easily established. Just as the air in the lecture hall evenly fills the lecture hall. Then inflation stretches a region that is large enough to include everything that we are now seeing. This is the first of my three proofs of inflation.

The second is what is called the problem of a flat universe. The question is, why was the early universe so flat? The question may immediately arise - what do I mean when I say that the early Universe was flat? One of the misconceptions that I sometimes encounter is that the flat is often perceived as two-dimensional. This is not what I mean. Flat does not mean like a two-dimensional pancake. The universe is three-dimensional. Flat in our case means Euclidean, obeys the axioms of Euclidean geometry, in contrast to the variants of non-Euclidean geometry, which are allowed by the general theory of relativity.
The general theory of relativity allows three-dimensional space to be curved. We consider only the uniform curvature. In reality, we see no curvature, but we know with greater accuracy that the universe is homogeneous than it is flat. So, imagine three possible curvature options for the universe, all of which will be considered homogeneous. Three-dimensional curved spaces are not easy to visualize, but all three of them are similar to two-dimensional curved spaces that are easier to imagine.

One of the options is the closed geometry of the surface of the sphere. The analogy is that a three-dimensional universe is analogous to a two-dimensional surface of a sphere. The number of measurements changes, but important things remain. So, for example, if you place a triangle on the surface of a sphere, and this can be easily visualized, the sum of its three angles will be more than 180 degrees. Unlike Euclidean geometry, where the sum is always 180 degrees.
STUDENT: Does the three-dimensional space bend in the fourth dimension? Just as two-dimensional models imply another dimension?
TEACHER: good question. The question was, does the three-dimensional curvature occur in the fourth dimension in the same way as the two-dimensional curvature occur in the third dimension? I think the answer is yes. But, I should clarify a little here. The third dimension from a purely mathematical point of view allows us to easily visualize the sphere. But from the point of view of people studying differential geometry, the geometry of a sphere is a clearly defined two-dimensional space without any need for a third dimension.
The third dimension is just a way for us to visualize the curvature. But the same method works for three-dimensional space. In fact, studying the three-dimensional curved space of a closed universe, we will do it that way. We use the same method, present it in four dimensions, and this will be very close to the two-dimensional picture you are looking at.
Thus, one of the possibilities is a closed geometry, where the sum of the three corners of the triangle is always more than 180 degrees. Another possibility is what is commonly called a saddle shape, or a space of negative curvature. In this case, the sum of the three corners, as they narrow, becomes less than 180 degrees. And only for a flat case, the sum of the three angles is exactly 180 degrees, which is the case of Euclidean geometry.
Geometry on the surfaces of these objects is not Euclidean, although if we consider the three-dimensional geometry of objects embedded in three-dimensional space, it is still Euclidean. But geometry on two-dimensional surfaces is not Euclidean on the top two surfaces, and Euclidean on the bottom surface.
This is how it works in the general theory of relativity. There are closed universes with a positive curvature and a sum of angles greater than 180 degrees. There are open universes where the sum of the three corners is always less than 180 degrees. And there is a case of a flat universe, which is on the border of these two, in which Euclidean geometry works. In our universe, Euclidean geometry works very well. That's why we all taught her at school. We have very good evidence that the early Universe was unusually close to this flat case of Euclidean geometry. This is what we are trying to understand and explain.
In accordance with the general theory of relativity, the geometry of the universe is determined by the density of mass. There is a certain value of the mass density, called the critical density, which depends on the rate of expansion, by the way, this is in no way a universal constant. But for a given expansion rate, you can calculate the critical density, and this critical density is the density that makes the universe flat. Cosmologists determine a number called Ω (Omega). Ω is simply the ratio of the actual mass density to the critical mass density. So, if Ω is 1, then the actual density is equal to the critical density, which means a flat universe. If Ω is greater than 1, then a closed universe will result, and if Ω is less than 1, the open Universe will be.

The evolution of the value of Ω is special because Ω is equal to 1, during the development of the Universe in ordinary cosmology, it behaves very much like a pencil balancing on its tip. This is an unstable equilibrium point. In other words, if Ω were exactly equal to 1 in the early Universe, it would remain exactly equal to 1. Just like a pencil, which is ideally placed on its tip, it will not know where to fall and in principle will remain in this position forever. At least in classical mechanics. We will not consider quantum mechanics for our pencil. For the analogy, we use a pencil of classical mechanics.
But if the pencil leans slightly in any direction, it will quickly begin to fall in that direction. Similarly, if Ω in the early universe were a little more than 1, it would quickly increase to infinity. This is a closed universe. Infinity in effect means that the universe reaches its maximum size, then begins to shrink and collapses. If Ω were a little less than 1, it would quickly decrease to 0, and the universe would simply become empty, as it would quickly expand.
Therefore, the only way for Ω to be close to 1 today, and as far as we can tell, Ω today is 1 - this is initially incredibly close to 1. It’s like that pencil that has stood for 14 billion years and hasn’t yet fallen. Numerically, in order for Ω to be somewhere in the allowable range very close to 1 today, it means that Ω one second after the Big Bang had to be equal to 1 with an incredible accuracy of 15 decimal places. This makes the density of the mass of the universe one second after the Big Bang, probably the most accurate number that we know in physics. We really know it to within 15 decimal places. If it were not in this range, then it would not be close to 1 today due to the amplification effect during the evolution of the universe.
The question is, how did this happen? In the usual Big Bang theory, theoretically, the initial value of Ω could be anything. To correspond to what we are seeing now, it should have been in this incredibly narrow range, but in theory there is nothing that would force him to be there. The question is, why was Ω originally so incredibly close to 1? As in the earlier mentioned problem of homogeneity, one can simply assume that it initially turned out to be what it should be, i.e. equal to 1. You can do so. But if you want to have some explanation of why this happened, there is nothing in ordinary cosmology that can explain it. However, inflation allows us to explain this.

In the inflationary model, the evolution of Ω changes, because gravity turns into a repulsive force instead of an attracting force, and this causes Ω to change differently. It turns out that during inflation, Ω does not move away from 1, as it did throughout the rest of the history of the universe, but, on the contrary, quickly moves to 1, exponentially fast. With this amount of inflation, which we talked about, inflation is about 10 28 times, it is enough that the value of Ω before inflation is not severely limited. Ω before inflation could not be 1, but could be 2 or 10 or 1/10 or 100 or 1/100.
The farther the initial Ω was from 1, the longer the inflation will be required to bring it sufficiently close to 1. But for Ω which is significantly different from 1, inflation will not take much longer, since inflation brings the omega to 1 exponentially. This is a very powerful force, bringing omega closer to 1. And this gives us a very simple explanation of why Ω in the early universe seemed to be extremely close to 1.
In fact, this prediction follows. Since inflation is so close to Ω to 1, we expect that today Ω really should be 1, or within the limits of the measured accuracy. You can imagine inflationary models, where Ω would turn out to be, say 0.2, this is what it was previously thought of, but to do this, inflation must end at exactly the right time before it gets even closer to 1. Because every exponential increase makes it even an order of magnitude closer to 1. This is a very fast effect. Therefore, without very careful adjustment, the majority of any inflationary models will bring Ω so close to 1 that today we see it as 1.
Previously, it seemed that it is not. Until 1998, astronomers were confident that Ω was only 0.2 or 0.3, while inflation had a fairly clear prediction that Ω should be 1. For me personally, this was quite a big inconvenience. Whenever I dined with astronomers, they said that inflation is a beautiful theory, but it cannot be correct, because Ω is 0.2, and inflation predicts Ω is 1. And this is just a discrepancy.
That all changed in 1998. Now the most accurate number for Ω that we have, obtained from the Planck satellite, along with some other measurements, is 1.0010, ± 0.0065. 0.0065 is an important thing. The number is very, very close to 1, and the margin of error is greater than this difference. Thus, today we know that with an accuracy of 0.5% or, maybe, 1%, Ω is equal to 1, which is predicted by inflation.
The new component that made all this possible, which changed the measured omega value from 0.2 to 1, is a new component of the energy balance of the Universe, the discovery of what we call dark energy. We learn a lot about dark energy during the course. The discovery in 1998 was that the expansion of the Universe does not slow down under the influence of gravity, as was expected before that time, but instead the expansion of the Universe is in fact accelerating.
This acceleration must be due to something. What causes this acceleration is called dark energy. Even though there are significant gaps in knowledge about dark energy, we can still calculate how much it should be in order to create the acceleration that we observe. And when all this is added together, we get a number that is much better consistent with inflation than the previous one.
STUDENT: Was the accelerating Universe unknown at that time a factor due to which it was incorrectly believed that Ω was 0.2 or 0.3?
TEACHER: Yes, it is. This was entirely due to the fact that it was not known about acceleration at that time. In fact, exactly measured the visible substance. This gave only 0.2 or 0.3. And this new component, the dark energy, which we know only because of acceleration, makes the necessary difference.
STUDENT: Is this data that makes Ω 0.2 or 0.3, really just a component of the Universe that we see through telescopes?
TEACHER: right. Including dark matter. In fact, we do not see everything. Without going into details now, we will discuss them later in the course; there is something called dark matter that is different from dark energy. Despite the fact that matter and energy are essentially the same, in our case they are different. Dark matter is matter, the conclusion about the existence of which we do because of its influence on another matter. Looking, for example, at the speed of rotation of galaxies, it is possible to calculate how much matter must be inside these galaxies for the orbits to be stable. It turns out that substances need much more than we actually see. This invisible matter is called dark matter, and it gives a contribution of 0.2 or 0.3. Visible matter is only about 0.04.
The next point I want to talk about is the heterogeneity of the universe on a small scale. On the largest scales, the universe is incredibly uniform - up to one thousandth, but on a smaller scale, the universe is extremely heterogeneous today. The Earth is a large cluster in the density distribution of the mass of the universe. Earth is about 10 30 degrees of times denser than the average density of matter in the universe. This is an incredibly tight clot. The question is, how did these clots form? Where did they come from?
We are confident that these bunches have evolved from the very minor disturbances that we see in the early universe, most clearly visible through cosmic background radiation. The mass density in the early universe, in our opinion, was homogeneous with an accuracy of about one hundred thousandth. But at the level of one hundred thousandth, we see that there are inhomogeneities in the cosmic background radiation.
Objects such as Earth have formed, because these small inhomogeneities in mass density are gravitationally unstable. In places where there is a slight excess of the density of a substance, this excess of density creates a gravitational field that attracts even more matter to these areas, which, in turn, produces an even stronger gravitational field that attracts even more matter. The system is unstable, it forms complex clusters that we see, such as galaxies, stars, planets, and so on.
This is a difficult process. But it all starts with these very weak discontinuities, which we believe existed shortly after the Big Bang. We see these inhomogeneities in the cosmic background radiation. Their measurement tells us a lot about the conditions in which the universe then existed and allows us to construct theories explaining how this universe came about. Satellites such as COBE, WMAP and Planck have been created to measure these inhomogeneities with very high accuracy.

Inflation answers the question of where the heterogeneity came from. In the usual Big Bang theory there was no explanation. It was simply assumed that the heterogeneities were there and they were added artificially, but there was no theory where they could come from. In inflationary models, where the whole substance is created by inflation, heterogeneities are also controlled by this inflation and appear due to quantum effects.
It is hard to believe that quantum effects can be important for the large-scale structure of the universe. The Andromeda Galaxy does not look as if it is a quantum oscillation. But if you look at this theory quantitatively, it really works very well. The theory is that the vibrations that we see in the cosmic background radiation were really purely a consequence of quantum theory, basically the uncertainty principle, which says that it is impossible to have something completely homogeneous. This is not consistent with the principle of uncertainty.
When we use the basic ideas of quantum mechanics, we can calculate the properties of these oscillations. To do this, we need to know more about very high energy physics, physics that was relevant in the period of inflation, in order to be able to predict the amplitude of these oscillations. We cannot predict amplitude. In principle, inflation would do this if we knew enough about the underlying particle physics, but we know too little about it. Therefore, in practice, we cannot predict amplitude.
However, inflationary models provide a very clear prediction of the spectrum of such fluctuations. By this I mean a change in the intensity of oscillations depending on the wavelength. Spectrum here means the same thing as for sound, except that you need to consider the wavelength, not the frequency, because these waves do not actually oscillate. But they have wavelengths just like sound waves, and, if we talk about the intensity of different wavelengths, the idea of the spectrum is really the same as in sound.

It can be measured. These are not exactly the last measurements, these are the last measurements for which I have a schedule. The red line is a theoretical prediction. Black dots are real measurements. This is a seven-year WMAP data. It is difficult to convey how happy I was when I saw this curve.

I also have graphs of what other theories predict. For a while, for example, people took very seriously the idea that the heterogeneities that we see in the Universe, these fluctuations, may have been caused by the random formation of so-called cosmic strings, which were formed in phase transitions in the early Universe. It was certainly a viable idea at one time, but as soon as this curve was measured, it turned out that the prediction of cosmic strings did not look like it at all. Since then, they have been excluded as a source of density fluctuations in the universe. Various other models are also shown here. I will not waste time on them, because there are other things that I want to talk about.

In any case, this is undoubted success. And this is the latest data. This is data from the Planck satellite, which was launched last March. I do not have it on the graph at the same scale, but again you see a theoretical curve based on inflation and points that show data with small tiny lines of errors. Absolutely clear match.
STUDENT: what happened to the theory of inflation after dark energy was discovered? Has it changed significantly?
TEACHER: Has the theory changed?
STUDENT: on the previous graph there was a different curve.
TEACHER: for inflation without dark energy. I think that not so much the theory of inflation is different for these two curves, but the curve that you see today is the result of inflation and the evolution that has occurred since then. And it is the evolution that has happened since then that makes a big difference between these curves.
Thus, the theory of inflation should not have changed much. And she really did not change. But, of course, the curve looks much better after dark energy was discovered, because the correct mass density became known, and gradually we got more and more data about these fluctuations that fit perfectly into what inflation predicts.

Now I want to go to the idea of the multiverse. I will try to quickly run through it so that we can finish. We still will not try to understand all the details now, so I will tell you about some of them in the remaining 10 minutes of the lecture. I want to talk a little bit about how inflation leads to the idea of the multiverse. We will come back to this at the very end of the course, and this is certainly a fascinating aspect of inflation.
Gravitationally repulsive material that creates inflation is metastable, as we said. He breaks up. This means that if you are in a place where inflation occurs, and ask yourself what the probability is that it will happen a little later, this probability decreases exponentially — it decreases twice in each doubling, each half-life. But at the same time, the volume of any area that swells up also grows exponentially, growing due to inflation. In fact, in any reasonable inflationary model, growth rates are much faster than rates of decay. If you look at the area that swells, if you wait for the half-life, half the volume of this area will no longer swell, by definition, the half-life. But the remaining half will be much larger than the volume with which we started. That's the whole point.
This is a very unusual situation, because it seems to have no end. The area that swells becomes more and more, even when it disintegrates, because expansion is faster than decay. This leads to the phenomenon of eternal inflation. The size of the swelling area increases with time, despite the fact that the swelling matter disintegrates. This leads to what we call eternal inflation. Eternal here means eternal in the future, as far as we can judge, but not eternal in the past. Inflation begins at some finite time, but then, as soon as it starts, it will continue forever.
Whenever a part of this swelling region goes through a phase transition and becomes normal, it locally looks like a Big Bang. Our Big Bang is one of these local events, and the universe formed by any of these local events where the expanding region disintegrates is called the pocket universe. Pocket simply because there are many such universes on the scale of this multiverse. They are in some sense small, although they are the same size as the universe in which we live. And our universe is one of those pocket universes.
Thus, instead of a single universe, inflation produces an infinite number of them. This is what we call the multiverse. It is worth noting that the word multiverse is also used in other contexts and other theories, but inflation, I think, is the most plausible way to build a multiverse. This is what most cosmologists have in mind when they talk about the multiverse.

What is the place of dark energy here? She plays a very important role. In 1998, two groups of astronomers, independently of each other, discovered that the universe is now expanding with acceleration. We now know that the universe has expanded rapidly over the past five billion years out of 14 billion years of universe history. There was a period when expansion slowed down to five billion years ago. The consequence of this is that inflation actually happens today. This accelerated expansion of the universe, which we see, is very similar to inflation, and we really interpret it as a similar kind of physics. We believe that it is caused by some kind of negative pressure, just as inflation was caused by negative pressure.
This matter, which apparently fills space and has negative pressure, we call dark energy. Dark energy is simply by definition something, whatever it is that causes this acceleration. One may ask, what is dark energy really about? The surest answer to this is nobody knows. However, there is the most plausible candidate. The most likely candidate, and other candidates are not very different from him, simply lies in the fact that dark energy is the energy of a vacuum. The energy of emptiness. It may be surprising that emptiness can have energy. But I will tell about it, and it is not so surprising.
But if dark energy is just vacuum energy, it fully corresponds to everything we know about the nature of the expansion of the universe, what we can measure.
STUDENT: why only in the last five billion years has the universe begun to expand rapidly?
TEACHER: I can now explain this. Now that I have said that there is probably vacuum energy, I can give you the answer. The answer is that the vacuum energy does not change with time, because it is just the vacuum energy. This is the same as I said about the energy density during inflation. This is just a constant. At the same time, ordinary matter becomes more discharged as the universe expands, reducing its density in proportion to the cube of the size of the universe.
It so happened that earlier about the last five billion years, ordinary matter dominated the universe, which created attracting gravity and caused the universe to slow down. But then, about five billion years ago, matter in the universe became so discharged that ordinary matter ceased to dominate the vacuum energy, and the vacuum energy began to cause acceleration. Vacuum energy was all the time, causing repulsion, but it was dominated by attracting gravity of ordinary matter until the last five billion years.

Now I want to talk, why can something be in the void? Why can emptiness have energy? The answer is actually quite clear to physicists today. Quantum vacuum, in contrast to the classical vacuum, is a very complex state. It is not at all empty. This is actually a complex set of vacuum oscillations. We think that even there is a field called the Higgs field, which you probably heard about, which on average has a non-zero value in a vacuum. Things like an electromagnetic field constantly oscillate in a vacuum due to the uncertainty principle, which leads to the presence of energy density in these fluctuations.
So, as far as we can judge, there is no reason for the vacuum energy to be zero. But this does not mean that we understand what its value is. Today, the real problem from the point of view of fundamental physics is not finding out why a vacuum can have a non-zero energy density. The problem is to understand why she is so small. Why is this a problem? Quantum field theory, which we will not study in detail, says that, for example, the electromagnetic field constantly fluctuates. This is due to the principle of uncertainty. These vibrations can have any wavelength. And each wavelength contributes to the energy density of the vacuum fluctuations.
There is no shortest wavelength. In a box of any size, there is the longest wavelength, but not the shortest wavelength. It turns out that when we try to calculate the vacuum energy density in quantum field theory, it diverges from the side of short wavelengths. It becomes literally infinite, since the formal calculation shows that all wavelengths contribute, and the shortest wavelength does not exist.
What does this mean in real physics? We believe that this is not necessarily a problem with our understanding of quantum field theory. In fact, we believe that this is only a limitation of the range in which our assumptions are correct. Of course, quantum theory works extremely well when it is tested in the laboratory. We think that at very short wavelengths something should limit this infinity. A good candidate for limiting infinity at short wavelengths is quantum gravity effects, which we do not understand.
Thus, one of the ways to estimate the true energy density predicted by quantum field theory is to limit the wavelength on the Planck scale, the energy scale, the length scale associated with quantum gravity, which is about 10 -33 centimeters. If you do this, then you can calculate the energy density of the electromagnetic field of a vacuum and get a finite number. But it is too big. It differs not by some small number, but very much. It is more by 120 orders of magnitude. Thus, we do not understand why the vacuum energy is as it is, since our simple estimates say that it should be 120 orders of magnitude larger.
It must be said that there is still a way out. The energy that we calculated here is only one of the contributions to the total vacuum energy. There are also negative contributions. If we calculate the fluctuation of the electron field, then its contribution to the energy will be negative. In principle, it is possible that these contributions accurately or almost exactly compensate each other, but we do not know why they should do this. Thus, there is a big question about the theoretical prediction of the vacuum energy density.

Now I want to tell a little about the landscape of string theory, which may be a possible explanation for the smallness of the vacuum energy. This is only a possible explanation, everything is very speculative here. But one possible explanation for this very small vacuum energy, which we observe, combines the idea of perpetual inflation and string theory. It is based on the idea that string theory does not have a unique vacuum. For many years, theorists have unsuccessfully tried to find a vacuum in string theory. They simply could not understand how the vacuum theory should look like in string theory.
And then, a little more than 10 years ago, many string theorists began to unite around the idea that maybe they could not find a vacuum, because there is no unique vacuum for string theory. Instead, they now claim that there are a huge number, they view numbers like 10,500 , an enormous number of metastable states that live long, any of which may look like a vacuum for a long period of time, even if it may eventually decay or go to one of the other metastable states. This is called string theory landscape. This huge set of vacuum states, any of which can be a vacuum, which, for example, fills in some pocket universe.
If we combine this with the idea of eternal inflation, then we can conclude that during the eternal inflation, all these 10,500 or more kinds of vacuum are likely to arise. That is, different pocket universes within themselves will have different types of vacuum, created randomly. Then we will have a multiverse, which will consist of many, up to 10,500 degrees or more different types of vacuums in different pocket universes.
With this assumption, string theory is the supposed law of physics that governs everything. But if you lived in one of these pocket universes, you would actually see the laws of physics, which were very different from the laws in other pocket universes. The fact is that the physics we actually see and measure is low energy physics compared to the energy scale of string theory. We see only small fluctuations in the structure of the vacuum in which we live.
So the particles that we see - electrons and quarks, which are combined into protons and neutrons, can be characteristic of our particular pocket universe. In other pocket universes there may be completely different kinds of particles that are oscillations of other kinds of vacuum. So, even if the laws of physics are the same everywhere - the laws of string theory, in practice, the observed laws of physics can vary greatly from one pocket universe to another. In particular, due to the fact that there is a different vacuum in different universes, the vacuum energy density may be different in different universes. And this gives a possible answer to why the observed vacuum energy is so small.
We will talk about this next time.
Source: https://habr.com/ru/post/411067/
All Articles