Cosmology - Stanford. Abstract. Lecture 1

This article opens a series of notes with notes on Cosmology at Stanford University. The English lectures themselves are available at: Cosmology (2013) - Leonard Susskind - Stanford University . Lecturer Leonard Susskind explains very accessible and fascinating. A talented person and an excellent teacher.

Stanford University is also famous for the fact that our distinguished compatriot Andrei Linde works there, who is likely to be awarded the Nobel Prize in Physics for his contribution to modern cosmology soon. Who cares, I advise you to watch his public lecture The many-sided Universe .

This summary is my attempt at self-education. I would have written it all the same for myself in a notebook. But I decided to combine business with pleasure. I hope that someone will be interested too.
')
Immediately make a reservation that I tried to take notes close to the original text. However, in some places I allowed myself to supplement or summarize the lecturer's remarks, drawing on my own experience as a physicist. This was done solely to promote understanding, understanding and assimilation of the material.

In this article, the summary of lecture 1 is offered to your attention. Continuing will appear gradually.

Historical overview

Cosmology is a very ancient subject. The history of cosmology goes back thousands of years. In particular, the ancient Greeks knew about cosmology for a very long time.

These lectures cover a period of time no further than the second half of the twentieth century, when Edwin Hubble discovered the law of expansion of the Universe.

If we talk about cosmology as a science, then this is a fairly new area of ​​knowledge. Modern cosmology originates from the discovery of microwave background radiation and the formulation of the big bang theory . And this happened only in the 1960s.

Up to this point, cosmology was not a division of physics, but rather belonged to the natural sciences. That is, in cosmology, the phenomenological approach prevailed: observation, measurement, classification, cataloging, etc.

At that time, the measurement accuracy was low. And therefore it was impossible to formulate precise statements. There were equations, but they were incorrect and inaccurate. Physicists have always been involved in the process of learning, since stars, galaxies and other celestial bodies have physical characteristics such as angular momentum, for example. Physical chemists have also been involved, since celestial bodies have a chemical composition.

However, the attitude to the Universe itself as a physical object, the Universe as a system that should be studied mathematically using a set of physical principles and the corresponding exact correct equations, is a relatively young approach.

Properties of the universe

In these lectures, the Universe is viewed as a physical system. And we will study it with the help of equations. We can start exploring the universe with some general observations.

Isotropy

So, the first observation, which, generally speaking, may not be absolutely accurate, just as all physics is not absolutely accurate - this is that the Universe is isotropic .

Isotropy means that the universe looks the same in any direction. Of course, this is true only for fairly large distances. If you look too closely, then isotropy may not be observed due to local inhomogeneities, for example, due to the shape of our galaxy.

Uniformity

If the Universe is isotropic, then it can be argued with a large degree of confidence that the Universe must also be homogeneous . Homogeneity means sameness not in every direction, but in every place. That is, on a large scale, the Universe looks the same regardless of where the observer is - in our galaxy or in some other one, which is far, far away from us.

Galaxies

Galaxies on the scale of the Universe are effectively mass concentration points . We can treat them as material points. The approximate number of galaxies in the visible part of the universe is one hundred billion. $$$10 ^ {11} = 100 \, 000 \, 000 \, 000$ . In turn, each galaxy also contains approximately $$$10 ^ {11}$ one hundred billion stars. We must remember that this number of galaxies is only inside the sphere that we can see. Only as far as astronomers can see with telescopes. That is, the most distant thing that we can see is at a distance, from where the light managed to reach us for the entire duration of the Universe: about 13 billion years.

Interesting fact. The total number of stars in the visible part of the universe $$$10 ^ {11} \ cdot 10 ^ {11} = 10 ^ {22}$ , and if each star has on average 10 planets, it turns out $$$10 ^ {23}$ - Avogadro number of planets in the Universe. Planetary mole of matter! (lecturer laughs)

Argument against the homogeneity of the universe. Denial

Consider a piece of the universe where we are. We know for sure because we see that the Universe is isotropic . We assume that the Universe is also homogeneous . But what would happen if the Universe were not homogeneous?

If the Universe is isotropic, then the only way for it to not be homogeneous at the same time is to have a structure in the form of a kind of shells.


Hypothesis of a heterogeneous universe. On the left isotropic homogeneous Universe, on the right isotropic non- uniform Universe. The cross in the center denotes us.

If this were the case, then at any other point the Universe would not look isotropic. That is, if we don’t want to believe that somehow we were exactly in the center of the Universe, and so that the whole Universe has spherical symmetry around us, then we will have to admit that the Universe is not only isotropic, but homogeneous.

Cosmological principle

So, if we do not believe that we are exactly in the center of the Universe, then the Universe must be homogeneous. The homogeneous Universe means that the Universe is uniformly filled with particles (galaxies) throughout its volume. This is called the cosmological principle . The cosmological principle is valid, because our observations indicate this, of course, to some extent approximation.

Some astronomers claim that they observed large-scale inhomogeneities in the universe. The lecturer doubts the reliability of these sources and statements.

Of course, the idea of ​​homogeneity of the universe is not absolutely accurate. Even the fact that there are galaxies, already suggests that there is heterogeneity. By the way, there are not only galaxies, but also clusters of galaxies. However, on a fairly large scale, about 1 billion light-years, the Universe looks homogeneous.

At first, the cosmological principle was only a postulate. But with the accumulation of observational data, it was confirmed more and more reliably, and in the end, the relic microwave radiation was discovered, which indicates that the initial distribution of matter in the Universe was highly homogeneous.

Setting a physical problem

There is a homogeneous gas from particles-galaxies. And each galaxy interacts with other galaxies. Galaxies as a whole are electrically neutral. But they are not neutral gravitationally. They interact through Newtonian gravity. And this is the only important force on a large scale. Gravity affects galaxies and tries to pull them all together.

So, if we consider any point in the Universe and ask ourselves where it should move, then we can guess that it is surrounded by the same amount of mass from all sides. Following this logic, we can assume that no galaxy should move at all, and the Universe should be static, since the resultant forces acting on any point in the Universe is zero. This is absolutely wrong!

And now we get the Newtonian equations of motion for the Universe. You may have heard that the expanding universe is in good agreement with Einstein’s general theory of relativity, and that before the general theory of relativity, the law of the expanding universe was incomprehensible. This is simply not true. Perhaps it was so historically. But this is only a historical fact about dates, not about logic. Newton could get the equations of an expanding universe. And we will now do it the way Newton should have done.

Coordinate system

In any physical problem, you must first enter the coordinate system. Instead of choosing the grid step as a distance: 1 meter, a million kilometers, a thousand light years, we will choose a coordinate grid so that its nodes are rigidly attached to the galaxies. Since the Universe is homogeneous, we can do it. Then the galaxies will always remain in approximately the same coordinates regardless of what happens to the Universe. That is, the galaxies like "frozen" in the coordinate grid.

It is not at all obvious that this can be done. If the galaxies moved completely randomly and in completely different directions, then we could not do that. But we see that galaxies are moving by chance. We see that galaxies move in concert, exactly as if they were embedded in some kind of coordinate grid. And what we see allows us to do this, because the speeds of galaxies relative to each other are consistent and not accidental.

We enter the grid $$$(x, y, z)$ . These coordinates are not measured in units of length. If we consider two galaxies separated by intervals $$$\ Delta x$ that distance $$$D$ between them (in meters) is expressed as

$$

$$D = a \, \ Delta x$$

Where $$$a$ - This is a scale parameter that can be a constant, and generally speaking, it may not be. The scale parameter may be time dependent. $$$a = a (t)$ .

Thus, by the Pythagorean theorem, the distance between two galaxies is generally written as

$$

$$D = a (t) \ sqrt {\ Delta x ^ 2 + \ Delta y ^ 2 + \ Delta z ^ 2}$$

And of course, the parameter $$$a$ is not constant. If it were a constant, then the galaxies would be static, they would not move anywhere. And this is not what we observe. We see that they fly apart from each other.

Hubble law

We write the relative velocity between the two galaxies. Let's differentiate the previous formula by time. We take into account that $$$\ Delta x$ - this is a fixed interval, which can not be changed according to the conditions of building a coordinate system. Then

$$

$$\ mathcal {V} = \ dot {a} \, \ Delta x$$

where we use the designation $$$\ dot {a} = da / dt$ .

We now write the ratio of the relative speed of two galaxies to the distance between them.

$$

$$\ frac {\ mathcal {V}} {D} = \ frac {\ dot {a} (t)} {a (t)}$$

Note that $$$\ Delta x$ is reduced, and this ratio does not depend on coordinates at all. That is, this formula is valid for any two galaxies no matter how far or close they are.

This ratio is called the Hubble constant parameter.

$$

$$H (t) = \ frac {\ dot {a} (t)} {a (t)}$$

and it does not depend on the coordinates. Then you can write the same thing in standard form.

$$

$$\ mathcal {V} = H \, D$$

The relative speed of two galaxies is proportional to the distance between them.

We need to understand that we would never have written this down if Hubble had not discovered his law. On the other hand, the Hubble Act is not so amazing. There is a saying: “There is nothing surprising in the fact that the fastest horse gallops ahead of everyone.” The faster you move, the farther you are. And this is a fact that Hubble discovered.

Mass of matter in the universe

Consider some volume $$$\ Delta x \, \ Delta y \, \ Delta z$ . Ask a question: what is the mass concentrated in this volume? Let be $$$\ nu$ - is the mass of the substance in the elemental volume $$$dx \, dy \, dz$ (in kilograms). Then the mass in volume $$$\ Delta x \, \ Delta y \, \ Delta z$ equals

$$

$$M = \ nu \, \ Delta x \, \ Delta y \, \ Delta z$$

What is the metric volume of this area? Because $$$D = a \, \ Delta x$ we can write

$$

$$V = a ^ 3 \, \ Delta x \, \ Delta y \, \ Delta z$$

What is the density of a substance in this area? By definition, the density is $$$\ rho = M / V$ that is, taking into account the two previous formulas, we obtain

$$

$$\ rho = \ frac {\ nu} {a ^ 3}$$

This is the standard physical density of a substance.

Although the total amount of mass in volume $$$\ Delta x \, \ Delta y \, \ Delta z$ does not change, since the galaxies are “frozen” into the coordinate grid, the absolute density of matter in the same volume can vary, since the parameter $$$a (t)$ depends on time.

Newton's theorem

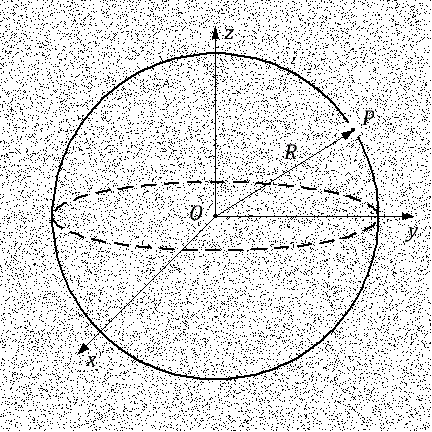
Illustration for Newton's theorem

Consider two galactites. We can always put one of them at the origin. Let galaxy $$$O$ is at the origin, and the galaxy $$$P$ is at some distance from it.

Newton's theorem states that the force of gravity acting on a galaxy $$$P$ depends only on the amount of mass inside the sphere with the center at the origin $$$O$ and passing through the galaxy $$$P$ . The second statement of Newton's theorem is that the whole mass inside this sphere can be considered concentrated in the center at the origin of coordinates at the point $$$O$ , provided that the mass inside the sphere is distributed, if not uniform, then at least isotropic .

In other words, the effect of the entire mass inside the sphere on the galaxy $$$P$ equivalent to as if this mass was concentrated at one single point $$$O$ which is the center of the sphere.

Newton's equations of motion

Find the distance between the galaxies $$$P$ and $$$O$ . Galaxy $$$P$ has coordinates $$$(x, y, z)$ that is, the distance from the center to the galaxy $$$P$ equally

$$

$$D = a (t) \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

We can enter the designation

$$

$$R = \ sqrt {x ^ 2 + y ^ 2 + z ^ 2}$$

$$$R$ measured not in meters, but in the same units as $$$x$ , $$$y$ and $$$z$ and does not depend on time. Then

$$

$$D = a (t) \, R$$

We now write the speed and acceleration of the galaxy $$$P$

$$

$$\ mathcal {V} = \ dot {a} (t) \, R$$

$$

$$\ mathcal {A} = \ ddot {a} (t) \, R$$

Now we must equate acceleration $$$\ mathcal {A}$ to acceleration associated with the entire gravitating mass inside a sphere of radius $$$R$ . Denote the mass of the galaxy $$$P$ behind $$$m$ and the mass of the whole substance inside the sphere is $$$M$ . Then the force of gravity acting on the galaxy $$$P$ equals

$$

$$F = -G \ frac {m \, M} {D ^ 2}$$

Where $$$G = 6.67408 \ times10 ^ {- 11} \ mathrm {N \ cdot m ^ 2 \ cdot kg ^ {- 2}}$ - gravitational constant. The minus sign in the formula means that it is gravity.

Now you can record the acceleration of the galaxy $$$P$

$$

$$\ mathcal {A} = -G \ frac {M} {D ^ 2}$$

Equate two expressions for $$$\ mathcal {A}$ and get

$$

$$\ ddot {a} (t) \, R = -G \ frac {M} {D ^ 2}$$

Consider that $$$D = a \, R$ then

$$

$$\ ddot {a} \, R = - \ frac {M \, G} {a ^ 2 \, R ^ 2}$$

Let's divide both parts by $$$a \, R$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {M \, G} {a ^ 3 \, R ^ 3}$$

Find the volume of the sphere

$$

$$V = \ frac {4} {3} \ pi \, D ^ 3 = \ frac {4} {3} \ pi \, a ^ 3 \, R ^ 3$$

Multiply the numerator and denominator of the right side by $$$4 \ pi / 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4} {3} \ pi \, G \, \ rho$$

This equation does not depend on $$$R$ and it is true for any galaxy in the universe. This equation is the central fundamental equation of cosmology .

One of the consequences of this equation is that it is impossible for the Universe to be static if it is not empty. From this equation it follows that the Universe can be static only if it is empty.

We can rewrite this equation, given that $$$\ rho = \ nu / a ^ 3$

$$

$$\ frac {\ ddot {a}} {a} = - \ frac {4 \ pi} {3} \ frac {G \, \ nu} {a ^ 3}$$

This equation was first obtained in the context of the general theory of relativity by Alexander Friedman. This equation does not tell us whether the universe is expanding or contracting. It only says that the second derivative of the scale factor is negative. That is, if the Universe expands, then it slows down, and if the Universe contracts, then it accelerates.

In fact, the universe is expanding and not slowing down. We only did what Newton could do and what all Cosmologists thought was right up until around 1998. This model was generally accepted and was called the standard model of the Universe until the accelerating expansion of the Universe was discovered. So far, there is only one term on the right side of the equation. In fact, there should be several terms that are related to the general theory of relativity.

Departure speed

Now we write the full galaxy energy $$$P$ as the sum of kinetic and potential

$$

$$E = \ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D}$$

The energy can be positive or negative, depending on the relationship between these two terms. It is also important to remember that the total energy of a particle $$$P$ preserved. If the total energy is positive, then the particle cannot turn back. A particle turns back only when the total energy is negative. The boundary case is that the total energy is zero. Solve the equation $$$E = 0$ for $$$\ mathcal {V}$ to find the departure speed.

$$

$$\ frac {1} {2} m \ mathcal {V} ^ 2 - G \ frac {m \, M} {D} = 0$$

$$

$$\ mathcal {V} _ {0} = \ frac {2MG} {D}$$

Just like a galaxy $$$P$ the whole Universe can have a speed higher than the speed of departure, less than the speed of departure or equal to the speed of departure. If the speed of the Universe is higher than the speed of departure, then it expands and never begins to shrink, but if the Universe has a speed lower than the speed of departure, then sooner or later it will shrink.

Rewrite the total energy equation

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = E$$

Friedmann equation

Consider the case when the speed of the universe coincides with the speed of departure.

$$

$$\ frac {1} {2} m \, \ dot {a} ^ 2 R ^ 2 - \ frac {m \, MG} {aR} = 0$$

Simplify the expression: divide by $$$m$ multiply by 2, divide by $$$a ^ 2 R ^ 2$

$$

$$\ frac {\ dot {a} ^ 2} {a ^ 2} - \ frac {2MG} {a ^ 3R ^ 3} = 0$$

In the second term, we multiply the numerator and denominator by $$$4 \ pi / 3$ . Then in the denominator we get the metric volume of the sphere $$$V$ . Considering that $$$M / V = ​​\ rho$ get

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} G \ rho$$

This is called the Friedmann equation . It is equivalent to the Newtonian equation obtained above. Since we assumed that the total energy is zero, such a universe expands, slowing asymptotically to zero, but never crosses zero and does not begin to contract.

Now remember what $$$\ rho = \ nu / a ^ 3$ . Rewrite the Friedman equation

$$

$$\ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi} {3} \ frac {\ nu G} {a ^ 3}$$

Parameter $$$\ nu$ very flexible.It depends entirely on our choice of grid. And, generally speaking, we could even choose it so that$$$\frac{8\pi}{3}\nu G = 1$ . Then

$$

$$\left(\frac{\dot{a}}{a}\right)^2 = \frac{1}{a^3}$$

The right side of this equation is always positive, and therefore the expansion rate
$$˙ a never becomes zero. Recall now that$\dot{a}$$$˙ a /a=His aconstantHubble parameter. It also follows from the equation that the Hubble parameter never changes sign. However, it still slows down. The Hubble parameter is getting smaller and smaller with time. This equation is extremely important for all cosmology. A simple way to solve it is to look for a solution of a certain type, namely, we will look for a solution in the form$\dot{a}/a = H$

$$

$$a(t) = c\,t^p$$

Where $$$c$ and $$p - some constants.$p$

$$

$$\dot{a} = c\,p\,t^{p-1}$$

$$

$$\frac{\dot{a}^2}{a^2} = \frac{p^2}{t^2}$$

$$

$$\frac{p^2}{t^2} = \frac{1}{c^3\,t^{3p}}$$

$$

$$3p = 2\\ p^2 = \frac{1}{c^3}$$

$$

$$p = \frac{2}{3}\\ c = \left(\frac{3}{2}\right)^{\frac{2}{3}}$$

We obtained the solution of the Friedmann equation.


The graph of the solution of the Friedmann equation. The

Real Universe follows this solution only up to a certain point in time, and then begins to accelerate. Newton could do it. He came very close. I asked all the right questions. The lecturer is confident that Newton, quite probably, did it and received this decision. However, such information about the universe went against his religious views, and therefore he did not publish his discoveries.