How to make impossible wallpapers: the history of forbidden symmetries

On the left - a sixth-order pattern of rotation of the wallpaper around each of the brown-green rosettes. On the right there is a pattern of wallpaper with mirror symmetry relative to the horizontal lines passing through each elliptical element of the stained glass ornament.

At first glance, to invent a wallpaper is no more difficult than doing tasks from kindergarten. Designers can choose any combination of colors and shapes for the original piece, and simply multiply it in two directions. Depending on the pattern of the initial piece and the choice of directions, additional symmetries may appear - for example, sixth-order symmetry in the first picture, or mirror one in the second. Both patterns are created by the mathematician Frank Faris from the University of California, Santa Clara.


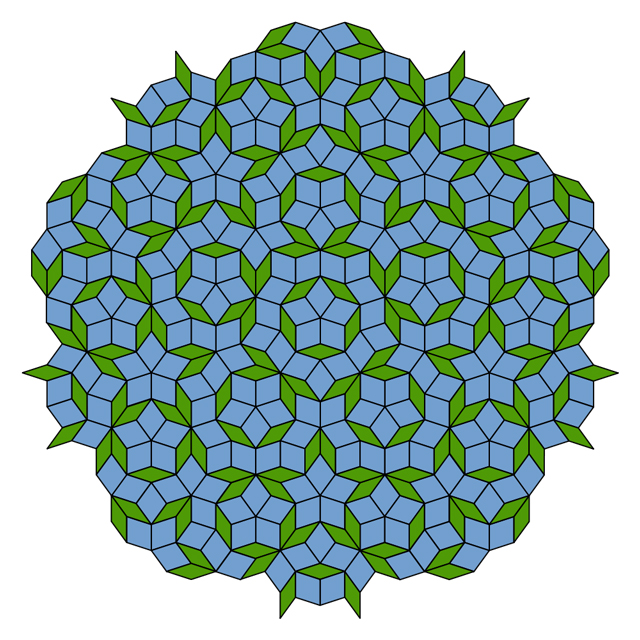
Penrose tiles show many examples of fifth-order local symmetry, but they have no pattern repetitions. When filling large areas on a plane, the ratio of the number of wide tiles to the number of narrow ones approaches the golden section.

But, although you can make wallpaper with rotational symmetries of the second, third, fourth or sixth order, it is impossible to create wallpaper with fifth-order symmetry [the order shows how many times during the 360 ​​° rotation the pattern will self-align itself - approx. trans.]. This limitation is known by mathematicians for almost 200 years as a "crystallographic constraint". The geometry of the pentagon forbids patterns with fifth-order symmetry. The same is true for orders of seven or more.
')
However, the most interesting patterns, such as Penrose tiles, exhibit fifth-order local symmetry in many places and on different scales, but without repeating patterns. Using a method different from Penrose's approach, Farris bridled the unusual fifth-order symmetry geometry and created a new set of exciting images - pseudo-wallpapers, not obeying, at first glance, crystallographic constraints.


Fig. four

The 4th figure looks like a counterexample for a crystallographic constraint, having fifth-order rotational symmetry around point A, while the pattern can be shifted in a plane in the directions AB or AC. In fact, Faris writes in his article for the journal Notices of the American Mathematical Society that this picture is just a clever fake.

“You know that the symmetry you are observing is impossible,” says Stephen Kennedy of Carleton College in Minnesota.

The rotational symmetry of the fifth order around point A seems to be satisfied. But if you look closely, you can see that the wheels around points B and C are slightly different from A. If we could move away from the pattern to see more repetitions, then visible repetitions of the pattern would be less and less like the pattern around the point And, even if more and more convincing copies of A would appear in other places, as in fig. 5. Faris showed that such illusions can be created on a larger scale, moving away from the pattern and repeating it a certain number of times — specifically, the number of times corresponding to numbers from the Fibonacci series (1, 1, 2, 3, 5, 8, 13, 21, ... where each following number is the sum of the two previous ones), which also plays its role in the geometry of Penrose tiles.


Fig. five

“By reason, we understand that this is some kind of deception,” says Faris. Nevertheless, as he writes in the article, these images "invite our view to study and enjoy them in almost perfect repetitions."

Faris thought of these fakes by changing the technology with which he created real wallpapers with rotational symmetry of the 3rd order, such as in fig. 6

To create 3rd order symmetry, Faris began work in three-dimensional space, which has one particularly natural rotation, sorting out three spatial coordinates, and rotating points in space 120 degrees around the diagonal. Then Faris created three-dimensional patterns of wallpaper, superimposing specially selected sinusoids and combining them with a pre-selected palette of colors. The points were colored depending on their position on the superimposed sinusoids. Then Faris brought out flat wallpaper, limiting this color to a two-dimensional plane, perpendicular to the intersection of the axis of rotation of the original space.

This smooth, sine-wave approach to creating wallpaper patterns is different from the traditional method of copying and pasting, Kennedy says. "This is a very new way to create symmetrical patterns."


Fig. 6

The same procedure, done in five-dimensional space, was supposed to lead to the creation of a pattern with fifth-order symmetry - if only we did not know that this was impossible. Interestingly, Faris thought, at what point does this system fail?

Theoretically, the five-dimensional space is possible, although it is difficult to imagine. It has a natural analogue of fifth-order rotation symmetry, as in three-dimensional space - the third symmetry. In five-dimensional space, you can choose one of two planes, each of which is perpendicular to the axis of rotation and the other plane. Each of them can be rotated around the point at 72 or 144 degrees. It may seem difficult to imagine two planes and a straight line, perpendicular to each other, but in five dimensions they all have enough space.

Faris realized what the problem is - if a perpendicular plane neatly cuts through three-dimensional space, and contains infinite wallpapers with an infinite number of points with integer coordinates, then two perpendicular planes in five-dimensional space are irrational, and do not contain points with integer coordinates (except for the reference point) . Since the wallpaper pattern created from sinusoids is repeated through shifts by integers, such planes do not inherit patterns from higher order spaces.

“This is how a fly appears in a soup,” Faris writes in an article.

However, on these two planes, the illusion of the structure of the wallpaper appears, thanks to the participation of the so-called. the golden section, an irrational number describing the directions of two planes, and Fibonacci numbers.

Thanks to their interrelations, Faris was able to show that although there are no points with integer coordinates on two planes, each of them comes very close to the infinite scattering of points with integer coordinates whose coordinates are Fibonacci numbers. Each time a plane approaches one of these Fibonacci points, the pattern looks almost the same as at the reference point, which creates the illusion of an exact copy.



Faris also thought up how to combine the colors and patterns of nature photos with wave functions in order to incorporate them into the design of patterns, as a result of which you can get a huge amount of "unreal" wallpapers. In the above figure, you can see the branches of trees, migrated from the photo.