Which figure of the same flat objects will look farther than the edge of the table?

In November, Quanta magazine puzzled its readers with questions regarding the compilation of figures from identical flat objects (such as coins or dominoes). This article provides both questions and detailed answers to them.

Question 1

In the classical task of constructing an overhanging figure, all blocks must be uniform, equal in size and shape, and their length is taken as one. At each level of the figure there can be only one block. Blocks cannot be joined or glued. If you have five such blocks, at what maximum length can the end of the top block lean out beyond the edge of the table on which they lie? Can you derive a formula for maximum overhang when using n blocks?

Physically, the task requires balancing the torque of the figure on both sides of the edge of the table. The torque of each side is the product of the mass of this side and the distance from the center of mass to the edge. When the center of mass of the whole figure is above the edge, the same moment acts on both sides of it, and the total torque of the system is zero. For a composite object, the total torque for any face can be found by adding the torque of all the component parts. Therefore, we can divide and conquer over the original task, considering only the changes that occur when adding a new block to an existing stack, something like mathematical induction (let's call it physical induction).

Consider a stack of n-1 blocks, each of which weighs one unit of weight and has a length of one unit of length. Pile balanced on the edge of the table. Imagine that the line of sight is directed along the edge of the table, and the table on the left — that is, the hanging ends of the blocks protrude to the right. Since the stack is balanced at the edge, the center of mass is directly above the edge, and its torque is zero. Now imagine that we lifted the whole stack vertically, and placed another block under it so that its right edge was flush with the edge of the table. In practice, this can be difficult, but in a thought experiment it is easy.
')
We added a bit of stability to the stack, adding the nth block from the bottom, since the center of mass of the whole stack shifted slightly to the left. We denote this offset x. n blocks weigh n units, and they have a total torque x * n around the edge of the table, pointing left. Recall that the total moment of a stack of n-1 blocks is zero. We have added only the moment of the new block - with a mass of one unit of mass and with a distance to the center of mass from the edge of the table to half the unit length.

It turns out that x * n = 1/2, which means x = 1 / 2n, where x is the distance to the new center of mass from the edge of the table.


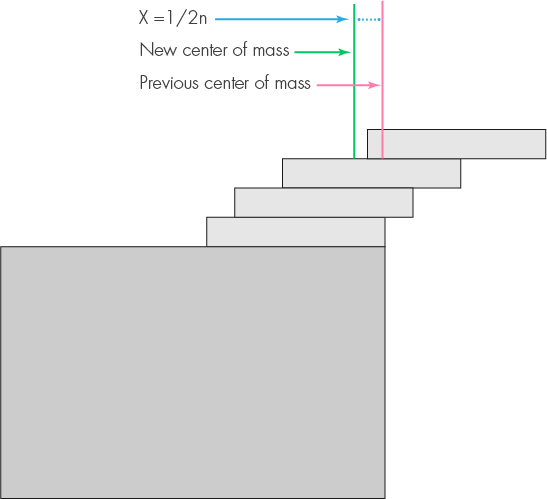
This means that if you move the entire stack of n blocks to the right by 1 / 2n length, it will be perfectly balanced at the edge - and this is the maximum possible shift. To complete the construction of induction, we note that the maximum overhang of the first block from the edge of the table is 1/2 units of length.

Therefore, for five blocks, we substitute in the formula n for each level from 1 to five to get the maximum overhang:

x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6) 

It can be seen that if you start from the top and then add blocks down, each shift will be half the reverse number of available blocks. Such sequences of inverse numbers are known as harmonic series. Such a series slowly diverges, and as n tends to infinity, it also tends to infinity.

The general sum formula for n blocks is obtained by summing all members of the series. It turns out half of the n-th harmonic term, which can be written as:

Question 2

Imagine that you have the same five blocks, and you want to put some kind of decoration on the topmost one, at a point that is a quarter of the block's distance from the hanging end. All blocks weigh one unit of weight, and the ornament weighs one-fifth of the block. What is the length of the maximum overhang? How does this change the basic formula?

First, consider the first block with the decoration on it, and lying so that its right edge is flush with the edge of the table. The center of mass of the block without decoration is half the unit length from the edge of the table. Decoration will move it to the right, for example, by x. The mass of the decoration is 1/5, and its distance from the new center of mass will be 1/4. Equate the moments and get x = 1/5 * (1/4-x), therefore, x = 1/24. Because of the decoration, it is necessary to move the first block to the left by 1/24 of the length, therefore the maximum overhang is now 11/24 instead of 1/2.


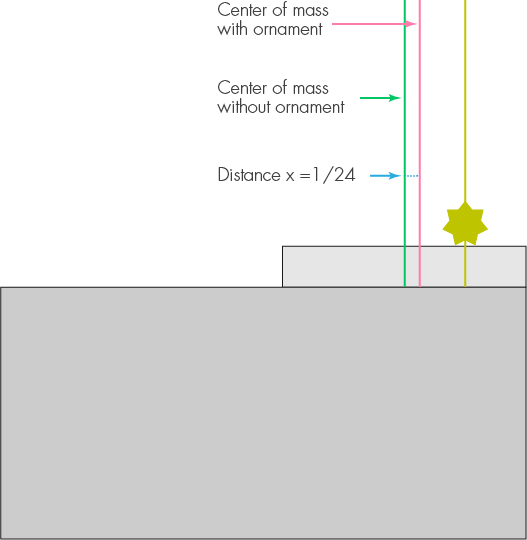
For subsequent blocks, you can apply the same induction as in the first question. We obtain the equation x (n + 1/5) = 1/2, which for n blocks is simplified to 1/2 (n + 1/5). This gives us the sequence 1/24 + 5/12 + 5/22 + 5/32 + 5/42 ..., which results in a maximum overhang of 1.057 for the five-level shape. Note that the overhang of the first block does not fit into the general scheme due to the additional weight of the decoration. However, a simple harmonic sequence appears through which the final sum can be easily calculated.

Question 3

Imagine that you are competing with a friend in a game in which you need to create overhanging structures. First you have one block. You place your blocks with any overhang from the edge of the table. Then you are given a random, but equal number of additional blocks from one to four. Each turn begins with the initial block as a basis, the position of which cannot be changed later, and with an additional set of one to four blocks. How much you need to move the initial block to the edge of the table so that you have the maximum possible overhang after a large number of moves?

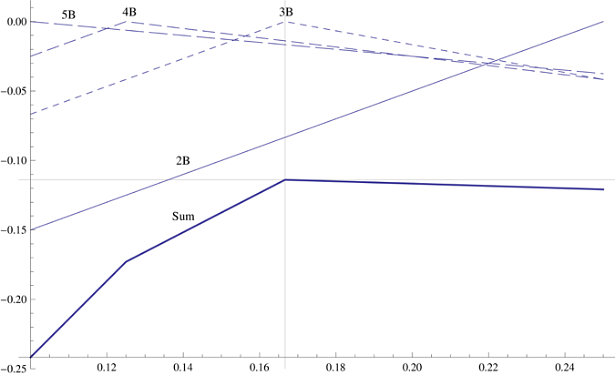
Since the probability of having from two to five blocks is the same, you need to maximize the amount representing the maximum overhang for these four cases. For a stack of 2-5 blocks there is an optimal position of the first block, which gives the maximum overhang of the entire stack. If you plot on the graph the largest overhang for each of the four possible sizes of the next stack, you will get two line graphs and two graphs in the form of an inverted V. Their vertices indicate the optimal initial position of the initial block for stacks of 3-4 blocks. Summing up the graphs, we obtain the overall overhang graph, which dramatically changes direction in each of the four optimal positions. It turns out that the best overall overhang is achieved in the optimal position for the three blocks, after which the graph goes down. Therefore, you need to have the original block in the assumption that you will be given three additional blocks, and the overhang will be 1/6 of a unit of length.


Readers pointed out several restrictions prohibiting this hypothetical mathematical bridge to go to infinity: wind, unevenness, lack of infinite accuracy, elasticity or insufficient hardness of the blocks and the table, etc. This, of course, is correct. To this can be added the curvature of the Earth and the absence of infinite space. Which of these restrictions fastest roll our pile? In order to answer this question, it is useful to study adjacent to it: if you forget about the overhangs from the edge and simply fold the Jenga blocks one on another, there is no mathematical restriction on the height of the tower. But its small imperfections in the blocks and inaccuracies in their construction will collapse, and the role of the last straw will be played by vibration or wind. The same is true for our dangling figure. If all these factors are corrected, at some point the rigidity of the blocks will also play, when the lower blocks warp slightly and move away from the horizontal due to the total torque of all the blocks above, which will lead to the upper blocks slipping.

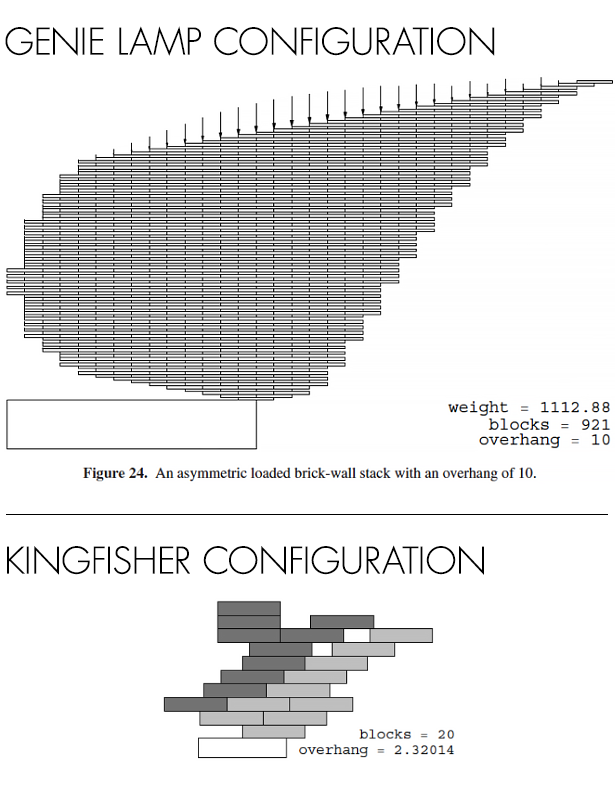
I mentioned that the greatest overhang can be achieved by allowing the use of several blocks on the same level. As several readers noted, the optimal solution to this problem is described in the 2009 work “ Maximum Overhang ” [ Maximum Overhang , by Paterson, Peres, Thorup, Winker and Zwick]. To me, small constructions made according to the Paterson-Zwick method resemble a kingfisher. The large ones look like magic lamps. For an overhang of two units of length, these schemes are 2-3 times more effective than classical harmonic overhangs, and reach such an overhang with the help of 14 blocks instead of 32. Unfortunately, their mathematics is too complicated for this article.