Musical theory for geeks

Someone considers music as a lot of selected talents, someone - a set of physical laws. The author of the material attempts to explain familiar musical terms to everyone, such as tone, interval, amplitude, note, octave, score, chord, and so on, using calculations and technical justifications. Below is a translation of the original text.

I don't know anything about music. I know that there are sign marks in music, but sometimes they grow squiggles. I know that increasing the octave doubles the pitch. I know that in order to write a song in the pop style, only four chords are enough. Here, perhaps, that's all.

All other rules for me look perfect, well, just completely arbitrary. Why do we have 12 notes, but only 7 letters are used to designate them? Where did the signs come from at the key? Why is it impossible to understand any single article on music on Wikipedia without first reading all the rest?

A few days ago, some of this finally cleared up. I feel like an idiot because I didn’t understand this before, but I suppose the whole thing is that everyone is trying to explain music to you using, ahem, musical notation that hardly makes any sense while you you do not understand why everything is arranged that way, and not otherwise.
')
Here I will tell you about the conclusions I made from the perspective of a person whose musical lessons were limited to trying to learn how to play 4 notes using a recorder in the second grade. I emphasize that I do not know anything about music. If you can at least whistle, please do not read this post, otherwise you will laugh at me.

Sounds and Waves

Music is a kind of sound. Sound is a pressure wave.

Imagine what happens when you beat the drum. When you beat it, its membrane, made of elastic material, deforms first inside, then bounces out, then inside again, and so on until it loses all its energy. If at this moment you observe a point in the center of the membrane, its movement will be very similar to what you get when you hold a toy walking spring (slink) at one end and let go of the other.

When the membrane bounces out, it pushes the air in front of it. This air pushes even more air in its path, which repeats the same action with the air molecules surrounding it, creating three-dimensional ripples emanating from the drum. Meanwhile, the membrane bounces inward, leaving behind a vacuum that is rapidly filled with ambient air, leaving another vacuum behind, and so on ... In the results, air molecules around the drum move back and forth relative to their initial position, just like the membrane or the spring of the link.

Ultimately, the pressure wave reaches your eardrums, which vibrate in the same way and you interpret these vibrations as music. Well, or as noise, depending on your tastes.

I would be happy to give an illustration of this process, but the fact is that it would look like a ripple on the surface of a pond, the waves of which at the same time move upwards . Sound vibrations occur in three dimensions, the movement is directed forward / away from the source of the oscillation, and this, in my opinion, is a very important difference.

So instead of illustrations, let’s go straight to the graphs and first take a look at the sine wave.

It doesn’t matter what a sine wave is . It is simple to depict it very easily on a graph and therefore it is convenient to cite as a typical example of a wave.

On charts like this, the time starts from zero and increases from left to right, and the wave shows how strongly the air (or your membranes, or other medium) has moved from its initial position. The complete silence on this graph can be displayed as a straight line going from left to right at zero level.

All sounds that you have ever heard, can be represented in the form of the same schedule. This is how simple it is. If you “open” a song in Audacity and zoom in on the graph, you will see a wave. It will most likely look somewhat more complicated, but it will still be a wave.

Any wave can be defined using several characteristics: frequency, amplitude and shape. Every sound you hear has some form that allows us to unmistakably distinguish the sound of a guitar and a violin. Musicians call this property the timbre .

A sine wave sounds like this :

Amplitude is the distance between the highest and lowest points of the wave. Well, or some experts define it as half of this value, that is, the distance between the highest point and zero. For our ear, the amplitude is the loudness of a sound, which is quite logical, because in terms of physics, amplitude is the largest numerical indicator of the deviation of the medium from the initial state. If you tap the membrane lightly, it will respond with a short wobble, and the sound will be quiet. If you start to play at full strength, then the vibrations of the membrane will become clearly visible, and the drum will sound much louder.

Frequency allows you to understand how often the wave literally repeats. If the waves on the graph are very thin, then it repeats more often, that is, its frequency is higher. If the wave crests are wide, then the wave repeats less frequently and its frequency is lower. Musicians call frequency pitch . Nemusykanta probably call it just a note or tone that will cause ridicule from the musicians, but what to take from them.

Frequency is measured in Hz (hertz). This is such a fun replacement for the phrase "per second." If it takes half a second to get from one point of the wave on the graph to the same point of the next wave, it is 2 Hz, because in a second, 2 waves “run through” the graph. In the above recording, you heard a 440 Hz sound. (The frequency of the wave on the graph, of course, is not the same. It shows a completely constant sine wave generated by wxMaxima, so its frequency is 1 / τ = 1 / (2π)).

An important property of the human ear, which determines many other musical patterns, is that if you double the frequency or frequency of the sound, then the resulting sound will seem to you in some sense "the same." Obviously, you will perceive it as a higher or lower , and yet you "feel" that it is very similar to the original sound. Of course, I can only guess about the physical nature of this phenomenon, but this rule is somehow very conditional.

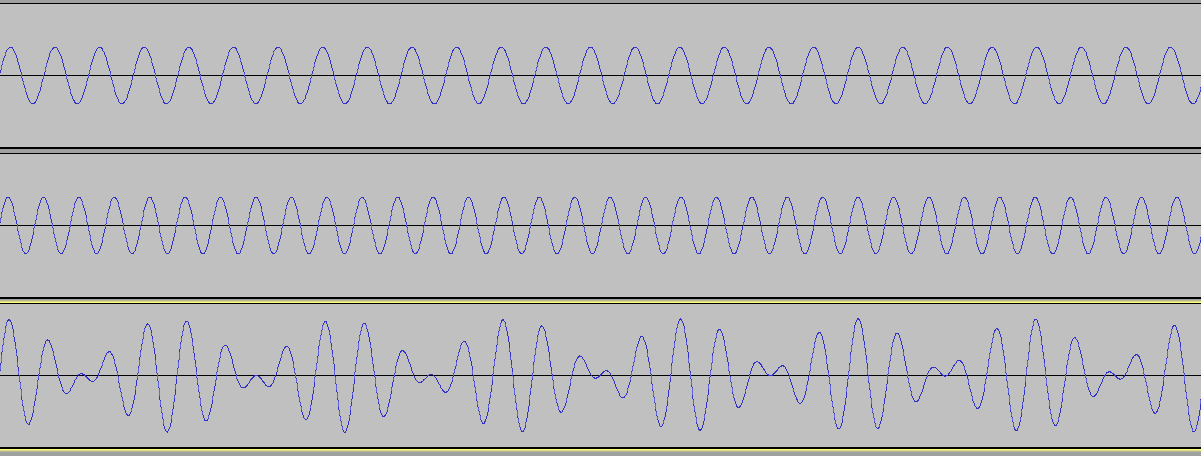
Compare these three sine waves if you want. The first is the same one shown earlier. The second frequency is 1.5 times more than the first, and the third frequency is doubled. The first and third are much closer in sound than the second in relation to both of them.

440 Hz wave
Wave frequency of 660 Hz
Wave frequency 880 Hz

Sheet music and octaves

The difficulty with musical theory lies in the fact that only half of the rules in it have a rationale, but the other half is quite arbitrary, and it is impossible to see the difference between these two categories at a glance.

Let's start with the following fact about human organs of hearing: if you first listen to the sound of the same height, and therefore double its height (that is, the frequency), then the second version will sound for us “just like the first one, but explain where this similarity we can not. Thus, for any initial tone f, you can create an infinite number of other tones that sound “also”: ½f, 2f, ¼f, 4f, and so on. Of course, only a finite amount of them will fall into the range of perception of the human ear. All of these tones together have some kind of common quality, so let's call them a group note .

Note can also be called a separate tone. Introducing such a thing as “tone class” would eliminate this ambiguity, but I will still continue to use the term “note” as a collective one .

If we accept that a frequency of 440 Hz reproduces a note called A, then 880 Hz, 220 Hz, 1760 Hz, 110 Hz and others will also correspond to a note called A. Hence the important conclusion: the frequency range of 440 Hz and 880 Hz is enough to identify all the notes we can come up with. The frequency of any other pitch can be increased or decreased by half until the value obtained falls within this range and becomes consistent with its note in it.

This range is called an octave . Why is it called so we will see a little later. Every note can exist only within a given octave, no matter how you call it. For example, the lowest f -tone is the same note as 2f , which, therefore, refers to the next octave.

And this is good news! This means that we can choose a certain group of tones whose frequencies lie within a small range - any small range of size f - 2f and increase or decrease their frequencies by half until we get a standard set of notes covering the entire range of human hearing.

In this regard, another question arises: by what rule will we choose these tones? You can offer a simple, at first glance, approach. For example, take all heights from f to 2f in increments of 0.1f and get the sequence f, 1.1f, 1.2f, 1.3f, 1.4f, and so on. What could be simpler and clearer than a uniform step?

Great plan! Unfortunately, in practice it does not work very well. Try it yourself and make sure that the difference in sound between f and 1.1f is not at all the same as the difference between 1.9f and 2f .

The human ear distinguishes pitch based on certain proportions (coefficients), which, in particular, explains the effect of doubling or dividing the frequency in half. The difference between f and 1.1f is 10%, whereas 1.9f and 2f differ from each other by only ~ 5%.

That is, it turns out, we need a set of tones with the same sound ratios between each other, and not the same difference in numerical measurement. If we need n tones, then we need to find such a number, multiplying that n times we can pass the entire range from f to 2f .

f × x × x × × ×… × x = 2f
fxⁿ = 2f xⁿ = 2 x = ⁿ√2

Wow. We need the nth root of the two. It is a bit strange and unusual, because the result will somehow be irrational for any n> 1.

Intervals in Western music

There are 12 different tones in western music. The choice of this value is largely arbitrary. That is, the twelve have, of course, some pleasant mathematical properties, but everything is not outstanding in it. You could easily invent your own set of notes with 11 tones, or 17th, or hundred or five. Some other musical forms used in other parts of the world do that.

The multiplication factor between consecutive tones in Western music is thus equal to the 12th power root of 2, or ¹²√2 ≈ 1.0594631. Taking, for example, the frequency of 440 Hz and sequentially multiplying it by this coefficient, we get 12 tones, the frequency of which does not exceed the value of 880 Hz.

In fact, no one wants to work with these numbers. When this system was invented, no one simply knew about them. Instead, in practice, musical terminology is based on ratios.

The ratio between the two tones is called the interval , and the interval is the size of the 12th root of the two - semitone . Using spacing allows you to throw all these terrible irrational numbers to hell, and we get the opportunity most of the time to speak the language of integers.

In fact, we work with a logarithmic scale. In fact, this only means that the concept of “add” turns into “multiply”.

And now remember that the human ear loves proportions. Especially nice are proportions consisting of small integers, which is why doubling the tone sounds “similar”: in this case, a 2 to 1 ratio is formed, the smallest of all integers you can think of.

Despite the fact that the 12th root of 2 is an irrational number, it is nevertheless almost ideal for creating several remarkable proportions. I don’t know why exactly 12 has such an effect, does the same happen with any other roots, but this is probably the very reason why Western music stopped at 12. Let's give data on the tones of all 12 notes and how they relate to the first tone of the scale. Some of these quantities are very close to the correct fractions.

Apart from the octaves, we get seven nice-looking fractions.

Hm Seven . What a remarkable number.

Gammas

Surprise! These seemingly pleasant ratios form a major scale . If we start from the note C (that is, before), we will get well-known to us "natural" notes, forming a gamut of C major (C major). Using the sign (the so-called sharp ), which means “increase by one semitone”, and ♭ (the so-called flat ), that is, “decrease by one semitone”, we can designate all the other notes.

I don’t know for sure, but I’d not be surprised if I find out that it is this kind of logic that I described here that led to the emergence of a modern system of naming sounds.

Now you can see where the names of some intervals come from. Net fifth (lat. Quinta - fifth ) - the interval between the first and fifth notes of the scale. Octave from (Latin Octava - eighth ) covers a total of eight notes. In the same way, the smallest interval received the name of a semitone, since the distance between the majority of notes was called a whole tone, and they themselves are two steps away from each other.

The intervals between successive notes can be recorded as tone-tone-semitone-tone-tone-tone-semitone. Since the octaves are repeated in a circle, you can create seven different variations, choosing any of the seven notes as the beginning of a sequence. The gammas obtained in this way are called diatonic, and the choice of the initial position is called the mode or tonality. I will give here all seven options. Roman numerals indicate the ordinal number of the degree of C-major, taken as the first in a particular column. The resulting notes look "natural."

Notice that the two columns are highlighted. In column number I you see the major scale ( gamma ), and in column VI - the natural minor scale ( gamma ). Now we can explain the origin of the names of the remaining intervals: a small ( minor, English ) third is the gap between the first and third notes of the minor scale, while a large ( major, English ) third is the interval between the first and third notes in the major scale. As for the fourth and fifth notes, the distance between them and the first note is the same in both types of scales.

(The same with the interval between the second and the first notes, and therefore the origin of the “minor (minor, English) seconds” is clear to me).

To create a major or minor scale, you can start from any note. It is only important to keep the same spacing pattern. The presence of 12 notes allows you to create a total of twenty-four major and minor scales, which is enough for a whole big and boring chart. I will give you several other major scales.

If you “rotate” these major scales so that they begin with C, they will look like this:

And here are a few minor scales recorded in the same form:

So what we see? Yes, each major gamma is equivalent to a minor one, if you start the countdown with the penultimate note. Such scales occur in parallel major and parallel minor .

And this notation has one little problem. It lies in the fact that the music recorded in scores is simply terrible.

Score and key marks

If you know something about a musical note, you probably noticed that no definite place is reserved for the recording of flat and sharp sharps.

That is, if you want to add other, raised or lowered notes, you do it on the same ruler , but with ♯ or ♭ next to them. Therefore, notes from D major, including F♯ and C♯, are written on the same ruler as F or C, but with ♯ added right in front of them. Writing this sign each time is not very convenient, so you can put it in the form of a sign at the key at the very beginning. Such a record looks like a few ♯ or ♭ recorded in certain places in order to indicate which notes should be raised or lowered. After that, any note not decorated with a similar designation will be considered raised or lowered by default.

And the notes themselves can be portrayed far from only as shown above. They also have squiggles that can connect them with other notes from above or below, which partly also depends on how the neighboring notes were drawn.

Well ... I guess ... is it convenient? If your music is almost entirely based on the use of seven notes of a certain scale, then it will be more compact to have a score designed for only 7 notes and adjust their designation to this system when needed ... yes?

However, this approach completely refutes the relationship between tones. Looking at some scores, you can’t even easily say in what key they are written, let alone memorize it all. In the above example, there are ♯ for C and F. But how exactly, looking at this designation, you must understand that it is about the key of “D major”?

Anyway, I touched on this topic just to draw your attention to the notation system. Let's look at C♯ major again:

It turns out that two pairs of notes use the same letter designation - C and C♯, F and F♯ and therefore occupy the same line in the score. The scheme of adding characters just described by me at the key does not allow doing this.

To remedy this situation, composers resort to a little trick. C is half a tone higher than B, so it can also be written as B♯. F is half a tone higher than E, so instead of F you can also write E♯. That is, this is how C♯ will look like in the end:

Due to this, all seven letters will be used in it only once.

I do not think that I fully understand the meaning of this approach, because it seems to me too sophisticated. That is, you need to turn C into C♯ in your mind, and after that you also need to translate C into that note that is actually played on your instrument in this case. What did the authors of this method try to achieve? Perhaps the only rational explanation for this that comes to my mind is the desire to keep the score of the score compact and fit exactly 7 notes.

I believe that by changing the key signs, you can change the sound of the entire piece of music. Sometimes this is enough, that is, after this action you don’t have to perform any additional manipulations at all. I wonder how this will affect the music, which also uses notes that go beyond the gamma used? However, this is rather a matter of composition, in which I absolutely do not understand anything.

Something there, something there and chords

Let's start to slowly get out of the wilds.

As I said, major and minor scales "go in pairs": each major scale has a "related" minor, having a completely identical set of notes and vice versa. So, C major is identical in A minor. Why do we need two identical scales at once? And more importantly, how can we even tell which of them is used in a particular piece of music, if both of them have the same set of characters on the key?

Many people tried to explain to me that parallel scales differ in mood, they have different sounds and a lot more of that, but all these arguments create new questions rather than answer questions already asked. I came to the conclusion that the correct answer consists of two parts.

The first part . When writing music, the composer pushes away from the key , which includes both the scale, and typical chords , and besides, there is a lot more of something else. A chord is a few notes that sound simultaneously or almost simultaneously. You can create many different chords, but the most popular of them are major chords and minor chords , which consist of the first, third and fifth notes of the scale. Chord C major (which is often for some unknown reason simply recorded as C), thus, consists of C, E and G, while the chord A minor (recorded as Am) consists of A, C and E.

Major chords consist of some pitch and two notes that are 4 and 7 semitones up from it, or, if it is even simpler, then {0, 4, 7}. Minor chords are {0, 3, 7}. The first and last notes in both types of chords are separated from each other by 7 semitones, that is, pure quint - thus a pleasant 3: 2 ratio. Major and minor chords with the same pitch are similar in sound, but the slightly lower middle note of the minor chord makes it sound a bit more dramatic or gloomy.

By the way, if you compare the major and minor scales starting with the same note, you will notice something interesting. They are very similar to each other, except that in a major three notes sound half a tone higher.

For each major and minor scale, you can make seven chords of this form, one for each note. For example, the second chord in the C major scale is a group of DFA notes, or simply D minor. Yes, it is minor. This is the same note order as in the first chord of the D minor scale.

Sometimes you will find chords recorded using Roman numerals. In such cases, the capital (large) characters are used to designate the notes that make up the major chords of a given key, and lower-case (small) ones for the minor. The chords of the major scale are recorded as I, ii, iii, IV, V, vi, and vii, the chords of the minor scale are i, ii, III, iv, v, VI, and VII. The number “I” merely means that a chord is constructed from the first note of the gamma, and so on. This notation allows you to talk, for example, about chord sequences , without worrying about the signs at the key.

Anyway, returning to the question of why we use both A minor and C major, we come to ...

The second part of the answer . It is just a custom. In Western music, there is a tendency to write works according to certain generally accepted standards, and people who are well versed in them can recognize which scale is involved in a particular case. The music recorded in C major will often begin with C or end on that note or even chord in C major. Music written in A minor will often begin with A or end on that note or A minor chord.

I believe that the advantage of this approach is the same as in the case of any other generally accepted norms: your work will be more accessible to other people from your field of activity. Transposing music from one key to another, for example, truly makes sense only if you can say with certainty which key signs were used initially. By the way, I recently got rid of an interesting link to the Für Elise performance in A major , instead of A minor, in which it was originally written.

And if you played it in C major, it would sound like ... uh ... stop, I'm confused.

Of course, it is not surprising that this generally accepted norm manifests itself in a huge number of very different nuances. For example, there is a harmonic minor scale , the seventh note in which is raised up to a semitone. In the melodic minor scale, the adjustments are made in several notes at once, but only in an ascending order, and not in a descending order. There are also increased chords (and intervals), the highest notes of which rise by a semitone, and reduced chords (and intervals), the highest notes of which, on the contrary, are reduced by a semitone. And so much more. All these nuances rather randomly overlap each other and create many conflicting names for the same concepts. At the same time, they themselves are more like attempts to describe human intentions than an objective form of sound vibrations.

There is such a thing called the " fifth circle ", which is a graphic display of all major and minor scales, where they are located in a circle. It turns out that if you name them and put them in the correct order, each scale will have a different number of sharps and flat. , , . « » . 7 ( «» ). , «» 7- , . , , , .

, , , , . . — A4 E5, 12- . , 3:2, 6 , .