The missing part: why physicists are forced to seek a quantum theory of gravity

Mathematics used in science in general and in physics in particular is often compared with language - and this creates the impression that it basically serves as a secret code for scaring strangers and that it is more inconvenience than a necessity. And although I support and highly appreciate the popularization of science, careful avoidance of technical terms and equations leads to the fact that mathematics is perceived as something optional, at best - cursive, and at worst - a tool of torture. But math is so much more.

Mathematics is first and foremost a discipline of thoughts. It is cleared of the uncertainty of the language and serves as a tool for deriving consequences from assumptions. She is not subject to human frailties, does not know pity and stands guard over objectivity.


')
Modern theoretical physics works by creating theories based on a set of assumptions or axioms, although they do not need to be clearly established and are sometimes given only implicitly. However, being formulated in mathematical terms, these assumptions lead to a much larger set of conclusions imposed on physicists. In order for a theory to become permissible in the sense of its applicability to the Universe, all these conclusions must be both internally consistent, that is, not to give rise to contradictions, and to coincide with observations.

To describe the most fundamental levels of nature at the moment, we have two theories - GTR and the Standard Model in Particle Physics. GRT is a classical theory, and the Standard Model is quantum field theory. The first does not obey the principle of uncertainty of Heisenberg, the second obeys. Together, two theories are capable of describing all existing observations, although some aspects of these descriptions do not quite satisfy us, for example, the missing microscopic structure of dark matter. The combination of the two theories coincides with the observations, but the trouble is that they do not agree with each other.



This discrepancy is best demonstrated by the problem of losing information in a black hole. Combining GR with quantum field theory, we get something called "quantum field theory in a curved space." It is partially classical, partially quantum, and therefore is called "semiclassical gravity." In this combined theory, it can be calculated that black holes emit radiation, called “Hawking radiation,” in honor of its discoverer.

Hawking radiation - the spectrum of a black body without special features and without defining parameters, except for one: its temperature, depending on the initial mass of the black hole. This means that all black holes with the same initial mass evaporate, producing exactly the same thermal radiation, regardless of what they are formed from. The process of formation and subsequent evaporation of a black hole is not reversible: even if we know everything about the final state, we cannot determine the initial state. Information is lost. The problem is that such an essentially irreversible process is incompatible with the quantum field theory used to derive this process: this is an internal contradiction, a discrepancy - and, therefore, nature cannot work this way. Mathematics imposed on us this conclusion.



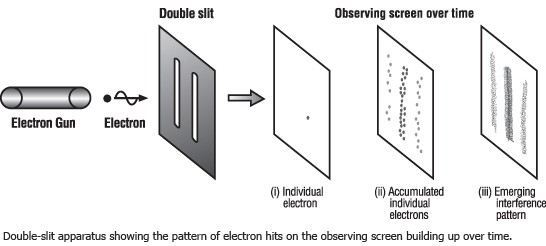
The semiclassical combination of GTR and the Standard Model leads to other problems. For example, we do not know what happens to the gravitational field of an electron passing through a double slit. We know that the electron wave function is in superposition and passes through both slots, creating a statistical distribution on the screen during the measurement. We also know that the electron carries energy. And we know that energy creates a gravitational field. But since the gravitational field is classical, it cannot be in superposition and pass through both slits, like an electron. What happens to the gravitational field of an electron? No one knows, because it is too weak to be measured. So simple and so insulting!



The third reason that convinces physicists of the incompleteness of the combination of GR and SM is that it leads to the appearance of singularities under fairly ordinary circumstances. Singularities - objects with infinite energy density and curvature. They are not physical and should not appear in a meaningful theory. They also appear, for example, in hydrodynamics, in the separation of a drop of water. But in the latter case, it is known that the singularity is an artifact of using approximations in hydrodynamics, which does not work at subatomic distances. At very short distances, one needs to use more fundamental theories (that is, the theory of quantum, individual particles) to describe a drop of water and there are no singularities in them, which is to be expected.



It is believed that the quantification of gravity solves these three problems, exposing the structure of space-time at ultra-short distances. Unfortunately, gravity cannot be quantified as other interactions of the standard model. If we apply these methods to gravity, then we come to the theory of "effective quantum gravity", which cannot solve these problems - it still breaks with strong curvature. This naive way (“perturbative”) quantified gravity is not suitable for solving problems with singularities and the evaporation of black holes, because it works only with weak gravity. It does not make sense as a fundamental theory. Speaking of "quantum gravity", physicists usually mean a theory that would work no matter how strong the gravity is.

There are several theoretical approaches to quantum gravity. The most famous of them are asymptotically safe gravity, loop quantum gravity, string theory and causal dynamic triangulation, as well as ideas that seriously relate to the hydrodynamic analogy and consider gravity a derivative phenomenon. So far, it is impossible to say which of the three approaches correctly describes nature.

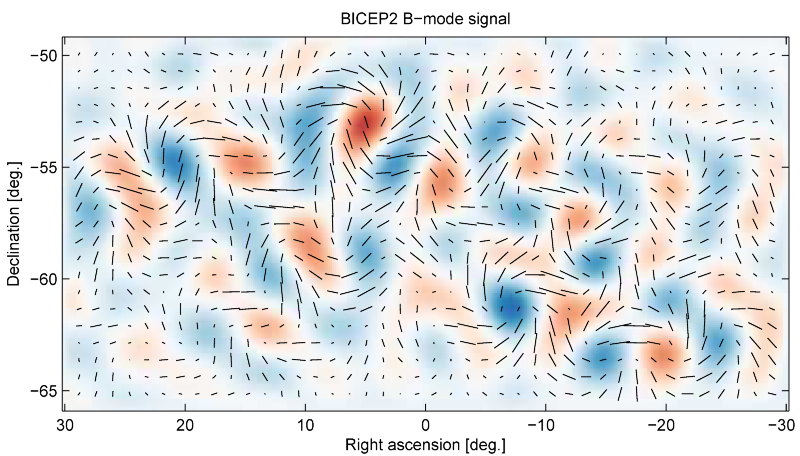
Following the traces of polarization measurements in the BICEP cosmic microwave background radiation (it is now established that this is only a consequence of the dust in the foreground), a statement was made that such a measurement would give us evidence of the quantification of gravity. This is not entirely true. First, this applies only to weak gravitational fields and therefore, not to the fundamental theory of quantum gravity. In addition, you need to be careful about the assumptions made for the sake of argument. Indeed, quantum gravitational fluctuations in the early Universe should have left an imprint on the background radiation, which in theory can be seen. However, it will be much more difficult to prove that quantum gravity is the only way to create observable fluctuations. Such a conclusion would require something like Bell's theorem, proof showing that the classical theory could not do this — and there is no such proof.



Quantum gravity is not such a large area for research as, say, condensed matter physics or cancer research. This is a small community, which nevertheless attracts a lot of public interest. And this is not in vain. Without quantum gravity, we do not know how space and time behave, and we don’t understand how our Universe began. We need a theory of quantum gravity to explain how space works and how it originated.

I also believe that this theory will give us important lessons on quantification, which will be useful to us in practice. If you listen to the adherents of string theory, then this process has already begun, regardless of whether string theory can solve the problem of losing information in a black hole!

The attractiveness of quantum gravity is due to the purity of the problem and the inevitability of mathematical logic, leading to the conclusion that there is no important part of the puzzle. We have to find out whether there will be enough purely mathematical approach to find this part. If not, our conclusions will remain ambiguous, and there will no longer be any guidance.