Treatise on entropy
Greetings to you, reader Hicktimes!
Many have heard of such a mysterious thing as entropy. Usually it is called a measure of chaos, a measure of uncertainty, and they also add that it certainly grows. I with great pain endure the use of the name of Entropy in vain and decided to finally write an educational program on this issue.
What happens if you throw a soccer ball to the ground? Obviously, he will bounce several times, with each next time at a lesser height, and then he will completely rest on the ground. And what will happen if you put a metal spoon in hot tea? The spoon will heat up, the tea will cool. Nothing complicated, is it? In each of these examples, the direction of the flow of processes seems obvious: the ball cannot bounce higher and higher and cannot even bounce forever to one height, and the tea cannot cool the spoon even more. From these everyday evidences, two postulates (of equal value) were derived, each of which can be equally called the second law of thermodynamics:
- the only result of any combination of processes cannot be the transfer of heat from a less heated body to a more heated one (Clausius postulate);
')
- the heat of the coldest of the bodies involved in the process cannot serve as a source of work (Thomson's postulate), i.e. the only result of any combination of processes cannot be the transformation of heat into work.
No wonder these two statements are called postulates, they are axiomatic, they cannot be proved, they are only confirmed by their consequences and all human experience.
It seems everything is clear: hot bodies cool down, cold ones heat up, energy dissipates. But what about another problem? Mixed by 1 mol of hydrogen, nitrogen and ammonia at a temperature of 500 o With in a reactor with a volume of 10 liters in the presence of a catalyst:

Which way will the reaction go: ammonia formation or decomposition? Mmm ... It seems we need more equations.
Every engineer knows thatin equal omega er efficiency more than in the Carnot cycle, it is impossible to achieve.
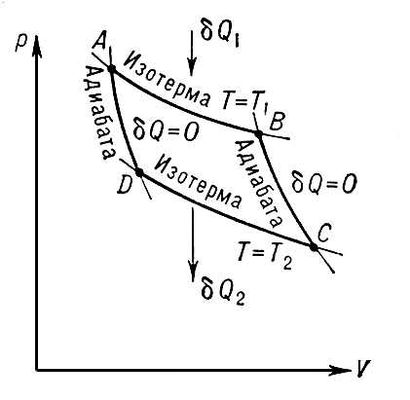
The cycle consists of two isotherms and two adiabats. Its efficiency is:

where Q n and Q x - the amount of heat received from the heater and given to the refrigerator, respectively, T n and T x - the temperature of the heater and refrigerator.
And now we will start mental gymnastics. Let us have two heat engines with different working bodies operating on the Carnot cycle. Moreover, the first one works equilibrium (i.e., at any time the system is in equilibrium, there are no turbulent flows and other things that reduce useful work and energy dissipating things; the work of the equilibrium process is always more non-equilibrium) and reversible (i.e., the process can to see: to conduct it in the opposite direction so that both in the system and in the environment become, as it was, an example of a reversible process is absorption and emission of a photon of the same wavelength by an electron, irreversible - body heating), and about the second unknown The first machine works in the opposite direction, i.e. using the work of the environment above it transfers heat from the refrigerator to the heater, the second works in the normal mode. Refrigerators and heaters of machines are connected, and the work done is equal in absolute value:

i.e., the work done by the second machine goes on transferring heat from the refrigerator to the heater first (remember that the heat received by the body is positive, the heat given to the environment is negative, the work done by the body is positive, the work perfect over the body is negative; in the efficiency formula all signs are already taken into account , therefore heat is taken modulo).
Let the efficiency of the second machine be greater than the efficiency of the first, then, taking into account (3), we have:


So, during all the vicissitudes and intricacies of the plot, the heater received the heat Qn I -Qn II , and the refrigerator gave the heat Q x I -Q x II . Both of these values are greater than zero, and the total work of both machines is equal to zero. That is, besides the fact that the heat was transferred from the refrigerator to the heater, nothing more happened ! Looking again at the postulate of Clausius, you can calm down and say that this does not happen.
It is logical to assume that condition (4) is incorrect, and therefore true:

If the second machine works equilibrium and reversible, then the system becomes symmetrical, i.e. the first and second cars can be swapped and nothing will change. Obviously, this case corresponds to an equal sign. From this we can conclude that the efficiency of a car operating in the Carnot cycle does not depend on the nature of the working fluid. Thus, to establish the efficiency formula, it suffices to consider any particular case. Equation (1) was obtained from the solution for an ideal gas. It can also be concluded that the efficiency (like the work) of a machine that works irreversibly and disequilibrium is less than that of a machine that works reversibly and in equilibrium.
From equation (1):

or

The algebraic sum of the relations between the heats of the process and their temperatures for the Carnot cycle is zero.
Any cyclic process can be divided into a set of infinitely small Carnot cycles, and then the previous condition will be transformed into:

Functions that change as a result of any cyclic process is zero are called state functions. Their value does not depend on the process path, but is determined only by the final state.
The function of the system state, the change in which during the equilibrium process is equal to the ratio of the heat of the process to its temperature, is called entropy:

(the equal sign refers to equilibrium processes, and the sign is greater to non-equilibrium).
If the system is isolated, that is, it does not exchange matter or energy with the environment, then Q = 0 (the system does not exchange heat with the environment), then:

or the entropy of an isolated system increases in non-equilibrium processes and remains the same in equilibrium, or the entropy of an isolated system does not decrease.
Amen. We have reached the very formulation of the second law of thermodynamics!
So, from the above, one cannot say that entropy is a measure of something, it is just a function. She always does not have to grow, nobody forbids herto kill to decrease.
Along the way, we decided the very same task about moths (yes, we’ll have to scroll back, I forgot it myself, after all, thermodynamics is an exciting thing!). To decide which way the reaction will go, you need to isolate the system and calculate the entropy change during the process: will decrease - will not go there, will increase - will go there, well, there is an option with balance to stop and rest.
Well, with a story about “entropy is always growing,” everything is clear: someone did not finish reading “an isolated system”, but hurried to carry the truth (c) to the masses. But what about the "measure of chaos"? I'll show you another approach.
Let us turn to statistics. Suppose we have N balls, which can be located at two different levels relative to the ground, the capacity of the first level is N 1 , the second is NN 1 . How many ways can these balls be placed? Obviously, this number of combinations without repetitions (the order of placement at the level is unimportant, but each ball is an individuality and is considered separately, you can present them numbered):

In fact, we recorded the number of microstates (the location of specific balls by level) through which it is possible to achieve the same macrostate (N 1 ball is at the first level relative to the ground, and N 2 balls at the second). Such a number is called thermodynamic probability. It differs from the usual probability in that it was forgotten to divide by the total number of microstates of all possible macrostates, i.e. if you vary N 1 and add all W with a constant number of levels and N.
Let's move from letters to numbers. Let the levels are still 2, there are only 40 balls, the levels are degenerate (i.e. the balls no matter what they are), and the balls randomly move between them. The thermodynamic probability of the distribution “20 there and 20 there” is 14.0 * 10 10 , and “19 to 21” - 13.3 * 10 10 . That is, the chance to see and see "20 to 20" is only 1.053 times more than "21 to 19", although intuitively we perceive the distribution in half as much more likely than the odds. That's what life-giving teverver does!
But we stared and that's enough, back to the topic of conversation. Thermodynamic probability also makes it possible to judge the course of the process: if we go from a state (macrostate), W of which is insignificantly small, to a state with a hugeCDW , then we can confidently say that the process will go. The reverse is also true. It remains to connect W and S. Nothing complicated, especially Boltzmann did it for us:

where k is the Boltzmann constant.
Finding such a connection, one can definitely say that with increasing entropy, the thermodynamic probability increases, that is, the number of options at the micro level increases, which realize one option at the macro level. Some people call such a huge number of options for the realization of one state chaos, but I can’t take it. All this "chaos" is subject to the laws and the Great Random, which is not chaos, but that Mr. Chance. I would call the entropy - in terms of the probabilistic approach - a measure of the invariance of the system, and I advise you to do the same!
The added fifth page in the word tells me that it is time to wrap up, although I would also like to say a few words about the limits of applicability of entropy, its character and the thermal death of the Universe. But this later, and now it's time to sleep ...
1. Gerasimov Ya.I. and others. "The course of physical chemistry", volume 1 - Moscow, from-in "Chemistry", 1964 - 624 p.
Many have heard of such a mysterious thing as entropy. Usually it is called a measure of chaos, a measure of uncertainty, and they also add that it certainly grows. I with great pain endure the use of the name of Entropy in vain and decided to finally write an educational program on this issue.
Second start
What happens if you throw a soccer ball to the ground? Obviously, he will bounce several times, with each next time at a lesser height, and then he will completely rest on the ground. And what will happen if you put a metal spoon in hot tea? The spoon will heat up, the tea will cool. Nothing complicated, is it? In each of these examples, the direction of the flow of processes seems obvious: the ball cannot bounce higher and higher and cannot even bounce forever to one height, and the tea cannot cool the spoon even more. From these everyday evidences, two postulates (of equal value) were derived, each of which can be equally called the second law of thermodynamics:
- the only result of any combination of processes cannot be the transfer of heat from a less heated body to a more heated one (Clausius postulate);
')
- the heat of the coldest of the bodies involved in the process cannot serve as a source of work (Thomson's postulate), i.e. the only result of any combination of processes cannot be the transformation of heat into work.
No wonder these two statements are called postulates, they are axiomatic, they cannot be proved, they are only confirmed by their consequences and all human experience.
It seems everything is clear: hot bodies cool down, cold ones heat up, energy dissipates. But what about another problem? Mixed by 1 mol of hydrogen, nitrogen and ammonia at a temperature of 500 o With in a reactor with a volume of 10 liters in the presence of a catalyst:

Which way will the reaction go: ammonia formation or decomposition? Mmm ... It seems we need more equations.
Cycle grandpa Carnot
Every engineer knows that

The cycle consists of two isotherms and two adiabats. Its efficiency is:

where Q n and Q x - the amount of heat received from the heater and given to the refrigerator, respectively, T n and T x - the temperature of the heater and refrigerator.
Word about cycle
So why is the efficiency of the Carnot cycle maximum, why can not think of anything more efficiently? By definition, efficiency is the ratio of useful work to expended. The cycle consists of two isotherms and two adiabats. With isotherms, everything is simple: since the internal energy of the system does not change during the isothermal process , all the heat obtained from the external environment goes to work, i.e. The efficiency of this particular process is 100%. There are two isotherms: one for the expansion of the working fluid (during this process, useful work is done), and the other for returning to its original state (during this process, the working fluid is compressed). Obviously, there is no point in carrying out both of these processes at the same temperature, since then all the energy received from the heater and spent on doing useful work, goes to the opposite process - compression. Again, it is better to compress according to the isotherm, because in this case, the heat given off to the refrigerator reduces only the volume of the system, but does not change the internal energy, i.e. to achieve the same degree of compression, it will be necessary to give less amount of heat, and this heat does not go to work (and is generally negative), i.e. reduces efficiency. Two adiabats are used to connect the two isotherms . During the adiabatic process, heat exchange with the environment is absent, the system does not receive heat, respectively, the efficiency does not decrease (it cannot increase due to the fact that the process-translator from one isotherm to another is repeated twice per cycle, but in different directions: all work that is done in the forward direction, will cost the opposite).
Thus, the heat received from the heater is spent on work, and then part of the work is spent on compressing the working fluid again along the isotherm (we will leave the work during adiabatic processes behind the brackets, it comes from the internal energy of the working fluid and is peacefully mutually destroyed). The smaller the second value, the greater the efficiency.
Thus, the heat received from the heater is spent on work, and then part of the work is spent on compressing the working fluid again along the isotherm (we will leave the work during adiabatic processes behind the brackets, it comes from the internal energy of the working fluid and is peacefully mutually destroyed). The smaller the second value, the greater the efficiency.
And now we will start mental gymnastics. Let us have two heat engines with different working bodies operating on the Carnot cycle. Moreover, the first one works equilibrium (i.e., at any time the system is in equilibrium, there are no turbulent flows and other things that reduce useful work and energy dissipating things; the work of the equilibrium process is always more non-equilibrium) and reversible (i.e., the process can to see: to conduct it in the opposite direction so that both in the system and in the environment become, as it was, an example of a reversible process is absorption and emission of a photon of the same wavelength by an electron, irreversible - body heating), and about the second unknown The first machine works in the opposite direction, i.e. using the work of the environment above it transfers heat from the refrigerator to the heater, the second works in the normal mode. Refrigerators and heaters of machines are connected, and the work done is equal in absolute value:

i.e., the work done by the second machine goes on transferring heat from the refrigerator to the heater first (remember that the heat received by the body is positive, the heat given to the environment is negative, the work done by the body is positive, the work perfect over the body is negative; in the efficiency formula all signs are already taken into account , therefore heat is taken modulo).
Let the efficiency of the second machine be greater than the efficiency of the first, then, taking into account (3), we have:


So, during all the vicissitudes and intricacies of the plot, the heater received the heat Qn I -Qn II , and the refrigerator gave the heat Q x I -Q x II . Both of these values are greater than zero, and the total work of both machines is equal to zero. That is, besides the fact that the heat was transferred from the refrigerator to the heater, nothing more happened ! Looking again at the postulate of Clausius, you can calm down and say that this does not happen.
It is logical to assume that condition (4) is incorrect, and therefore true:

If the second machine works equilibrium and reversible, then the system becomes symmetrical, i.e. the first and second cars can be swapped and nothing will change. Obviously, this case corresponds to an equal sign. From this we can conclude that the efficiency of a car operating in the Carnot cycle does not depend on the nature of the working fluid. Thus, to establish the efficiency formula, it suffices to consider any particular case. Equation (1) was obtained from the solution for an ideal gas. It can also be concluded that the efficiency (like the work) of a machine that works irreversibly and disequilibrium is less than that of a machine that works reversibly and in equilibrium.
From equation (1):

or

The algebraic sum of the relations between the heats of the process and their temperatures for the Carnot cycle is zero.
Any cyclic process can be divided into a set of infinitely small Carnot cycles, and then the previous condition will be transformed into:

Functions that change as a result of any cyclic process is zero are called state functions. Their value does not depend on the process path, but is determined only by the final state.
The function of the system state, the change in which during the equilibrium process is equal to the ratio of the heat of the process to its temperature, is called entropy:

(the equal sign refers to equilibrium processes, and the sign is greater to non-equilibrium).
If the system is isolated, that is, it does not exchange matter or energy with the environment, then Q = 0 (the system does not exchange heat with the environment), then:

or the entropy of an isolated system increases in non-equilibrium processes and remains the same in equilibrium, or the entropy of an isolated system does not decrease.
Amen. We have reached the very formulation of the second law of thermodynamics!
So, from the above, one cannot say that entropy is a measure of something, it is just a function. She always does not have to grow, nobody forbids her
Along the way, we decided the very same task about moths (yes, we’ll have to scroll back, I forgot it myself, after all, thermodynamics is an exciting thing!). To decide which way the reaction will go, you need to isolate the system and calculate the entropy change during the process: will decrease - will not go there, will increase - will go there, well, there is an option with balance to stop and rest.
Well, with a story about “entropy is always growing,” everything is clear: someone did not finish reading “an isolated system”, but hurried to carry the truth (c) to the masses. But what about the "measure of chaos"? I'll show you another approach.
The second father
Let us turn to statistics. Suppose we have N balls, which can be located at two different levels relative to the ground, the capacity of the first level is N 1 , the second is NN 1 . How many ways can these balls be placed? Obviously, this number of combinations without repetitions (the order of placement at the level is unimportant, but each ball is an individuality and is considered separately, you can present them numbered):

In fact, we recorded the number of microstates (the location of specific balls by level) through which it is possible to achieve the same macrostate (N 1 ball is at the first level relative to the ground, and N 2 balls at the second). Such a number is called thermodynamic probability. It differs from the usual probability in that it was forgotten to divide by the total number of microstates of all possible macrostates, i.e. if you vary N 1 and add all W with a constant number of levels and N.
Let's move from letters to numbers. Let the levels are still 2, there are only 40 balls, the levels are degenerate (i.e. the balls no matter what they are), and the balls randomly move between them. The thermodynamic probability of the distribution “20 there and 20 there” is 14.0 * 10 10 , and “19 to 21” - 13.3 * 10 10 . That is, the chance to see and see "20 to 20" is only 1.053 times more than "21 to 19", although intuitively we perceive the distribution in half as much more likely than the odds. That's what life-giving teverver does!
But we stared and that's enough, back to the topic of conversation. Thermodynamic probability also makes it possible to judge the course of the process: if we go from a state (macrostate), W of which is insignificantly small, to a state with a huge

where k is the Boltzmann constant.
Word about equation
The derivation of this equation is also simple. Entropy likes to take shape, and probabilities — multiplying means:

The khmkhm product is equal to / equal to / equal to the sum of khmmkhm. A familiar ratio? And it seemed familiar to Boltzmann! And he derived on the sheet the equation of the name of himself with the constant name of himself. The latter, incidentally, is also easy to find: we have not limited in any way until now (and we will not) the set of objects that obey this equation, and for all these objects the constant is the same, which means we can take a special case, calculate the constant for him and approve her candidacy. By the way, the ideal gas was again selected as a special case.

The khmkhm product is equal to / equal to / equal to the sum of khmmkhm. A familiar ratio? And it seemed familiar to Boltzmann! And he derived on the sheet the equation of the name of himself with the constant name of himself. The latter, incidentally, is also easy to find: we have not limited in any way until now (and we will not) the set of objects that obey this equation, and for all these objects the constant is the same, which means we can take a special case, calculate the constant for him and approve her candidacy. By the way, the ideal gas was again selected as a special case.
Finding such a connection, one can definitely say that with increasing entropy, the thermodynamic probability increases, that is, the number of options at the micro level increases, which realize one option at the macro level. Some people call such a huge number of options for the realization of one state chaos, but I can’t take it. All this "chaos" is subject to the laws and the Great Random, which is not chaos, but that Mr. Chance. I would call the entropy - in terms of the probabilistic approach - a measure of the invariance of the system, and I advise you to do the same!
The added fifth page in the word tells me that it is time to wrap up, although I would also like to say a few words about the limits of applicability of entropy, its character and the thermal death of the Universe. But this later, and now it's time to sleep ...
Literature
1. Gerasimov Ya.I. and others. "The course of physical chemistry", volume 1 - Moscow, from-in "Chemistry", 1964 - 624 p.
Source: https://habr.com/ru/post/396999/
All Articles