Mate horse and elephant. Solution Base
Want to puzzle the novice chess player?
Ask him to checkmate with a horse and an elephant.
Want to puzzle a novice programmer?
Ask him to calculate the mat horse and elephant.

')
Chess problems excite the programmer's imagination,
that is why for practical demonstration of combinatorics
I chose the most difficult chess problem from the “checkmate to the lonely king” cycle.
The goal of the project is to create a decision base, that is, a list of correct moves for all possible arrangements of the white king, bishop, and black king on the chessboard.
In this publication, I will tell you how I solved this problem, what difficulties I had to face, and also to demonstrate what eventually happened. Technologies used: C #, JavaScript, PHP, HTML, CSS.
Being a very mediocre chess player, I never learned how to quickly checkmate with a knight and an elephant. Therefore, I decided to compensate for this lack with my programming skills, go through all possible positions and find the right move for each.
Before writing at least a line of code, I had a “Napoleon” plan for several weeks, as I would do. I really wanted to start to solve this problem from the end, with the search of all matte combinations. And then make one move backward until all possible options have been exhausted.
On the chessboard 64 cells. We have four figures.
The number of possible combinations is 64 * 64 * 64 * 64 = 16,777,216.
You can leave only the light-squared elephant.
The number of options will be halved: 64 * 32 * 64 * 64 = 8,388,608.
So many positions will be in our database of solutions.
In fact, there are even fewer combinations: two figures cannot stand on one square, kings cannot stand on neighboring squares, the black king cannot be under check, and so on. Looking ahead, I will say that in the database of solutions there were 5,609,790 combinations, the array will be 67% full.
However, in order to simplify the algorithm and speed up access to the database data, I decided to “not waste time on trifles” and create a four-dimensional array for all combinations.
For the storage of each combination, the following structure is defined:
Inside, another Coord structure is used to record the coordinates of the figure, with the possibility of calculating the index from 0 to 63, as well as with the overloaded comparison operator.
This structure turned out to be very convenient for passing as an argument to various auxiliary functions, for example:
However, it’s not enough to record the result of the decision base of this structure;
The goal of our program will be the creation of a “white box”, into which all positions will be formed, in which the “white move”, and for which it is known, what kind of move needs to be made and how many moves will be mated with guarantee.
An integral part of the “white box” is the following structure:
For the organization of the "white box" the easiest way to open a four-dimensional matrix. Each dimension of this matrix corresponds to the possible position of each figure:
The first dimension is the coordinate of the white king.
the second dimension is the coordinate of the white elephant / 2.
the third dimension is the coordinate of the white horse.
the fourth dimension is the coordinate of the black king.
The main thing is not to confuse their order :) The array will turn out to be 33% discharged, but very convenient for processing. It is in this array that 8,388,608 records will be stored for solving combinations.
By the way, before starting to write all the brute force algorithms, I created an empty project and initialized this four-dimensional matrix in order to make sure that there is enough memory and no need to reinvent something else. Apparently, the experience of participation in Olympiads in computer science of the past millennium, where the size of the structure could not exceed 64 kilobytes, has affected, because Turbo Pascal 7.0.
I will briefly describe the main idea of solving this problem. It is based on the search algorithm in breadth, which had to be slightly modified, since two people play chess and the moves are made in turn. Therefore, instead of one queue, we will need two - “black” and “white”.
With the structure of WhitesMove, we have already met. The structure of BlacksMove is a bit simpler, since there is no need to keep Black’s last move in it.
First, in the “black line” we will place all the dull positions in which the black moves. Then from each such position we will make a reverse move for White and form a “white line” - a list of positions in which White’s move.
These actions will need to be repeated until all possible combinations have been fully exhausted.
The main algorithm in the form of pseudocode:
Creating the base of the correct moves begins with a search for all matte combinations. The use of enumerators made it possible to quite effectively describe this process.
Total found 232 matte positions. Let me remind you that we have limited ourselves to the light-squared elephant.
Some of them are quite exotic, non-existent and “cooperative”, this is when the black king himself crawled under the mat.

Chess players are well aware that the horse knight and the squared elephant must be placed in the white corner. In the black corner, checkmate is possible only if black plays along. I specifically posted a photo with just such a pseudomat at the beginning of the article to provoke the attention of real chess players :)
The next stage is to make White's return. That is, for each matte position found, make all possible White's reverse moves .
How to make a return stroke? Considering that the taking in our positions is not provided for, the algorithm is quite simple - to make any white move, after which there will be no check to the black king.
All positions found in this way can already be put in a “white box”, indicating that there is one move to the mat and which move is needed to do this. Along the way, we put the found combinations into a “black queue”.
This is what this part of the algorithm looks like:
A total of 920 such positions were found, here are the most interesting:
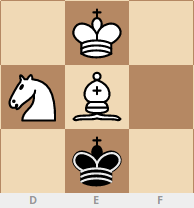
The knight's move:


Elephant move:
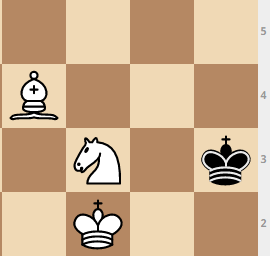

King move:
The next stage is to reverse the move of black. With this algorithm, I was carrying the longest, a lot of mistakes were made before everything worked correctly.
At first glance, everything is similar to the previous version: for each position from the “white line”, it is necessary to sort through all possible moves of the black king. And adding all the found combinations to the “black line” - this is a mate in one and a half moves, from which it will be possible to do the reverse move for White again - there will be mate in two moves - and so continue until all options are reviewed.
That was the mistake. With any possible move by black, a “cooperative” mate is obtained in one and a half moves, and in fact the king will not necessarily go under the mate. Dmitry Grin, who attended all of my webinars to create this program, pointed me to this error, for which we thank him separately.
The correct algorithm is as follows: for each position N, after the black king has reversed, one must go through all his possible direct moves to make sure that all of them lead to familiar positions from the “white box”, that is, lead to the mat. And only after this, the N position can be added to the “black queue”. And if from position N the black king can “slip away”, then this option is skipped. She will meet on subsequent iterations, when there will be more familiar positions.
This is what this part of the algorithm looks like:
A total of 156 “One and a Half Turn Mat” combinations were found.
The described algorithms for creating semi-moves must be looped. From the “black line” we form a “white line”, and then vice versa - from the “white” line we form a “black”. And so on until all new positions are exhausted. The “white box” is filled at the stage of the formation of the “white line”, since it places the positions in which the white move.
The finished algorithm went through all the options for about 12 minutes and stopped at 33 moves. That is the maximum number of moves needed to mate the black king with a knight and an elephant from any position.
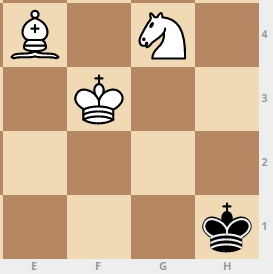
By the way, there were not so many such “most difficult” positions, only 156, here’s one of them:

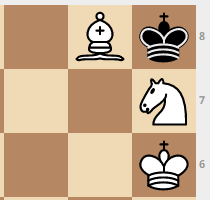
There are quite a few positions in which even after White’s move, the black king can eat a horse or an elephant and get a draw. There are also stalemate options. Here are some of the most interesting positions.



How to store the found solution database?
The easiest and wrong way is to use serialization. The serialized four-dimensional array of the structure took 1.7 gigabytes (!) On the disk. The serialization process lasted about six minutes, it took about the same for deserialization.
This option, of course, does not fit. In addition, in practice there is no need to use the entire four-dimensional array. For a specific position, only one entry is needed.
Eureka! To save space, you can still get rid of storing the coordinates of the figures for each combination. When we have a four-dimensional array, the position of each piece on the board is uniquely determined by its index in the array.
It was decided to store the entire database of solutions in a single file - as a linear scan of a four-dimensional array. For any possible position, an address is calculated at which the correct answer is recorded.
How to compactly write down the answer we need? The position of the figures is not necessary to store, so there are only three numbers left - how many moves to the mat, what to go and where to go. That is exactly what determines the correct move for White.
6 bits How many moves to the mat is an integer from 0 to 33.
2 bits. Which figure walks - three possible options, a king, an elephant or a horse.
6 bits Where the figure goes - the field index on the board is from 0 to 63.
This means that two bytes are enough for each solution record:
1 byte - how many moves to the mat, or 0 if the position is unfamiliar.
2 bytes - FFNNNNNN
FF - the number of the figure to walk (1 is the king, 2 is the elephant, 3 is the horse)
NNNNNN - cell coordinate - where to go (from 0 to 63).
So, the solution database file is 64 * 32 * 64 * 64 words = exactly 16 megabytes. The placement of the figures is given by the coordinates of each word, in the first byte - the number of moves to the mat (or 0 if there is no solution), the correct move is stored in the second byte.
It would be possible to further reduce the file size by half, if you do not store the number of moves to the mat, but it will not be interesting to play.
It's time to pay for optimization. It is necessary to implement the coordinate recalculation algorithm for combinations with the “black and white” elephant.
This was done as follows. If the elephant's coordinate falls on a black field, then the coordinates of all the pieces on the board must be "turned over." In this case, the Y coordinate remains unchanged, and X changes to 7-X. A visual demonstration of the flipping of coordinates, see the figure.

If the elephant is on a white cage, then first you need to "flip" the coordinates of all the figures. Then search for a position in the database of decisions. And once again “turn” the coordinate of the correct move read from there.
So, the Problem is solved!
Solution database is created.
But how to demonstrate it?
The most obvious way is to use web technologies so that you can simply give a link to a working example. The “ Nano-chess ” photo course was already created on my “programmer’s formula”, where an interactive chess board was created for the game together with no rules using the HTML, CSS, JavaScript and PHP technologies. This script was taken as a basis.
I left only four figures, removed the possibility of taking, added PHP functions for reading the correct moves from the decision base and “breathed life” through JavaScript.
On www.videosharp.info/chess, you can experiment with the decision base.

For each position, the moves are calculated for both white and black.
For whites - the best move that leads to the mate.
For blacks - how many moves to mate on any possible move.
With the mouse you can make any movements of the figures, not necessarily according to the rules.
The script will calculate the option for any position, or write that there are no options.
It is interesting to play, performing the proposed moves or moving the pieces at their discretion.
A great, interesting work was done on solving a chess problem.
If you want to repeat this path - you can watch videos on the creation of this program from scratch to the result with detailed explanations and independent tasks.
Good luck!
Ask him to checkmate with a horse and an elephant.
Want to puzzle a novice programmer?
Ask him to calculate the mat horse and elephant.

')
Chess problems excite the programmer's imagination,
that is why for practical demonstration of combinatorics
I chose the most difficult chess problem from the “checkmate to the lonely king” cycle.
Goal setting
The goal of the project is to create a decision base, that is, a list of correct moves for all possible arrangements of the white king, bishop, and black king on the chessboard.
In this publication, I will tell you how I solved this problem, what difficulties I had to face, and also to demonstrate what eventually happened. Technologies used: C #, JavaScript, PHP, HTML, CSS.
Being a very mediocre chess player, I never learned how to quickly checkmate with a knight and an elephant. Therefore, I decided to compensate for this lack with my programming skills, go through all possible positions and find the right move for each.
Before writing at least a line of code, I had a “Napoleon” plan for several weeks, as I would do. I really wanted to start to solve this problem from the end, with the search of all matte combinations. And then make one move backward until all possible options have been exhausted.
How many options are there?
On the chessboard 64 cells. We have four figures.
The number of possible combinations is 64 * 64 * 64 * 64 = 16,777,216.
You can leave only the light-squared elephant.
The number of options will be halved: 64 * 32 * 64 * 64 = 8,388,608.
So many positions will be in our database of solutions.
In fact, there are even fewer combinations: two figures cannot stand on one square, kings cannot stand on neighboring squares, the black king cannot be under check, and so on. Looking ahead, I will say that in the database of solutions there were 5,609,790 combinations, the array will be 67% full.
However, in order to simplify the algorithm and speed up access to the database data, I decided to “not waste time on trifles” and create a four-dimensional array for all combinations.
For the storage of each combination, the following structure is defined:
struct Combo { public Coord whiteKing; public Coord whiteBishop; public Coord whiteKnight; public Coord blackKing; } Inside, another Coord structure is used to record the coordinates of the figure, with the possibility of calculating the index from 0 to 63, as well as with the overloaded comparison operator.
public struct Coord { public byte x; // 0 7 ( a h) public byte y; // 0 7 public int index { get { return x + y * 8; } set { x = (byte) (value % 8); y = (byte) (value / 8); } } public static bool operator == (Coord a, Coord b) { return ax == bx && ay == by; } } This structure turned out to be very convenient for passing as an argument to various auxiliary functions, for example:
bool isCheck (Combo combo); // bool isCheckmate (Combo combo); // bool isCheckByBishop (Combo combo); // However, it’s not enough to record the result of the decision base of this structure;
White box
The goal of our program will be the creation of a “white box”, into which all positions will be formed, in which the “white move”, and for which it is known, what kind of move needs to be made and how many moves will be mated with guarantee.
An integral part of the “white box” is the following structure:
struct WhitesMove { public Combo combo; public byte moves; // public Coord moveFrom; // - public Coord moveTo; // } For the organization of the "white box" the easiest way to open a four-dimensional matrix. Each dimension of this matrix corresponds to the possible position of each figure:
WhitesMove [ , , , ] box = new WhitesMove [64, 32, 64, 64]; The first dimension is the coordinate of the white king.
the second dimension is the coordinate of the white elephant / 2.
the third dimension is the coordinate of the white horse.
the fourth dimension is the coordinate of the black king.
The main thing is not to confuse their order :) The array will turn out to be 33% discharged, but very convenient for processing. It is in this array that 8,388,608 records will be stored for solving combinations.
By the way, before starting to write all the brute force algorithms, I created an empty project and initialized this four-dimensional matrix in order to make sure that there is enough memory and no need to reinvent something else. Apparently, the experience of participation in Olympiads in computer science of the past millennium, where the size of the structure could not exceed 64 kilobytes, has affected, because Turbo Pascal 7.0.
The idea of the algorithm
I will briefly describe the main idea of solving this problem. It is based on the search algorithm in breadth, which had to be slightly modified, since two people play chess and the moves are made in turn. Therefore, instead of one queue, we will need two - “black” and “white”.
Queue<BlacksMove> blackQueue = new Queue<BlacksMove>(); Queue<WhitesMove> whiteQueue = new Queue<WhitesMove>(); With the structure of WhitesMove, we have already met. The structure of BlacksMove is a bit simpler, since there is no need to keep Black’s last move in it.
struct BlacksMove { public Combo combo; public byte moves; } First, in the “black line” we will place all the dull positions in which the black moves. Then from each such position we will make a reverse move for White and form a “white line” - a list of positions in which White’s move.
These actions will need to be repeated until all possible combinations have been fully exhausted.
The main algorithm in the form of pseudocode:
" ", " ", " " " " { " " " " " " " " " " " " " " " " " " } " " " " Matt Positions
Creating the base of the correct moves begins with a search for all matte combinations. The use of enumerators made it possible to quite effectively describe this process.
foreach (Combo combo in AllCheckmates()) { BlacksMove checkmate = new BlacksMove { combo = combo, moves = 0 }; blackQueue.Enqueue(checkmate); } Total found 232 matte positions. Let me remind you that we have limited ourselves to the light-squared elephant.
Some of them are quite exotic, non-existent and “cooperative”, this is when the black king himself crawled under the mat.

Chess players are well aware that the horse knight and the squared elephant must be placed in the white corner. In the black corner, checkmate is possible only if black plays along. I specifically posted a photo with just such a pseudomat at the beginning of the article to provoke the attention of real chess players :)
Checkmate one move
The next stage is to make White's return. That is, for each matte position found, make all possible White's reverse moves .
How to make a return stroke? Considering that the taking in our positions is not provided for, the algorithm is quite simple - to make any white move, after which there will be no check to the black king.
All positions found in this way can already be put in a “white box”, indicating that there is one move to the mat and which move is needed to do this. Along the way, we put the found combinations into a “black queue”.
This is what this part of the algorithm looks like:
// " " while (blackQueue.Count > 0) { // " " BlacksMove black = blackQueue.Dequeue(); // foreach (WhitesMove white in AllWhiteBackMoves(black)) // if (!isCheck(white.combo)) // " " if (!whiteBox.Exists(white.combo)) { // " " whiteBox.Put (white); // " " whiteQueue.Enqueue(white); } } By the way, about yield
The use of enumerators with the yield mechanism allows for very nice implementation of various iterations, for example, this is how the function looks through all possible moves with white pieces:
IEnumerable<WhitesMove> AllWhiteBackMoves(BlacksMove black) { foreach (WhitesMove white in AllWhiteKingMoves(black)) yield return white; foreach (WhitesMove white in AllWhiteBishopMoves(black)) yield return white; foreach (WhitesMove white in AllWhiteKnightMoves(black)) yield return white; } A total of 920 such positions were found, here are the most interesting:
The knight's move:



Elephant move:


King move:

Mate in one and a half turn
The next stage is to reverse the move of black. With this algorithm, I was carrying the longest, a lot of mistakes were made before everything worked correctly.
At first glance, everything is similar to the previous version: for each position from the “white line”, it is necessary to sort through all possible moves of the black king. And adding all the found combinations to the “black line” - this is a mate in one and a half moves, from which it will be possible to do the reverse move for White again - there will be mate in two moves - and so continue until all options are reviewed.
That was the mistake. With any possible move by black, a “cooperative” mate is obtained in one and a half moves, and in fact the king will not necessarily go under the mate. Dmitry Grin, who attended all of my webinars to create this program, pointed me to this error, for which we thank him separately.
The correct algorithm is as follows: for each position N, after the black king has reversed, one must go through all his possible direct moves to make sure that all of them lead to familiar positions from the “white box”, that is, lead to the mat. And only after this, the N position can be added to the “black queue”. And if from position N the black king can “slip away”, then this option is skipped. She will meet on subsequent iterations, when there will be more familiar positions.
This is what this part of the algorithm looks like:
// " " while (whiteQueue.Count > 0) { // N " " WhitesMove white = whiteQueue.Dequeue(); Combo whiteFigures = white.combo; // N foreach (BlacksMove black in AllBlackBackMoves(white)) { bool solved = true; // foreach (Coord blackKing in AllKingMoves(black.combo.blackKing)) { whiteFigures.blackKing = blackKing; // if (isCheck(whiteFigures)) // continue; if (box.Exists(whiteFigures)) // continue; solved = false; // "" break; } // // " " if (solved) // " " blackQueue.Enqueue(black); } } A total of 156 “One and a Half Turn Mat” combinations were found.
Iteration of semi-moves
The described algorithms for creating semi-moves must be looped. From the “black line” we form a “white line”, and then vice versa - from the “white” line we form a “black”. And so on until all new positions are exhausted. The “white box” is filled at the stage of the formation of the “white line”, since it places the positions in which the white move.
The finished algorithm went through all the options for about 12 minutes and stopped at 33 moves. That is the maximum number of moves needed to mate the black king with a knight and an elephant from any position.
By the way, there were not so many such “most difficult” positions, only 156, here’s one of them:

Mata will not be!
There are quite a few positions in which even after White’s move, the black king can eat a horse or an elephant and get a draw. There are also stalemate options. Here are some of the most interesting positions.




How to store the solution database
How to store the found solution database?
The easiest and wrong way is to use serialization. The serialized four-dimensional array of the structure took 1.7 gigabytes (!) On the disk. The serialization process lasted about six minutes, it took about the same for deserialization.
This option, of course, does not fit. In addition, in practice there is no need to use the entire four-dimensional array. For a specific position, only one entry is needed.
Eureka! To save space, you can still get rid of storing the coordinates of the figures for each combination. When we have a four-dimensional array, the position of each piece on the board is uniquely determined by its index in the array.
It was decided to store the entire database of solutions in a single file - as a linear scan of a four-dimensional array. For any possible position, an address is calculated at which the correct answer is recorded.
How to compactly write down the answer we need? The position of the figures is not necessary to store, so there are only three numbers left - how many moves to the mat, what to go and where to go. That is exactly what determines the correct move for White.
6 bits How many moves to the mat is an integer from 0 to 33.
2 bits. Which figure walks - three possible options, a king, an elephant or a horse.
6 bits Where the figure goes - the field index on the board is from 0 to 63.
This means that two bytes are enough for each solution record:
1 byte - how many moves to the mat, or 0 if the position is unfamiliar.
2 bytes - FFNNNNNN
FF - the number of the figure to walk (1 is the king, 2 is the elephant, 3 is the horse)
NNNNNN - cell coordinate - where to go (from 0 to 63).
So, the solution database file is 64 * 32 * 64 * 64 words = exactly 16 megabytes. The placement of the figures is given by the coordinates of each word, in the first byte - the number of moves to the mat (or 0 if there is no solution), the correct move is stored in the second byte.
It would be possible to further reduce the file size by half, if you do not store the number of moves to the mat, but it will not be interesting to play.
Coordinates of the black white elephant
It's time to pay for optimization. It is necessary to implement the coordinate recalculation algorithm for combinations with the “black and white” elephant.
This was done as follows. If the elephant's coordinate falls on a black field, then the coordinates of all the pieces on the board must be "turned over." In this case, the Y coordinate remains unchanged, and X changes to 7-X. A visual demonstration of the flipping of coordinates, see the figure.

If the elephant is on a white cage, then first you need to "flip" the coordinates of all the figures. Then search for a position in the database of decisions. And once again “turn” the coordinate of the correct move read from there.
Solution Base Visualization
So, the Problem is solved!
Solution database is created.
But how to demonstrate it?
The most obvious way is to use web technologies so that you can simply give a link to a working example. The “ Nano-chess ” photo course was already created on my “programmer’s formula”, where an interactive chess board was created for the game together with no rules using the HTML, CSS, JavaScript and PHP technologies. This script was taken as a basis.
I left only four figures, removed the possibility of taking, added PHP functions for reading the correct moves from the decision base and “breathed life” through JavaScript.
On www.videosharp.info/chess, you can experiment with the decision base.

For each position, the moves are calculated for both white and black.
For whites - the best move that leads to the mate.
For blacks - how many moves to mate on any possible move.
With the mouse you can make any movements of the figures, not necessarily according to the rules.
The script will calculate the option for any position, or write that there are no options.
It is interesting to play, performing the proposed moves or moving the pieces at their discretion.
Conclusion
A great, interesting work was done on solving a chess problem.
If you want to repeat this path - you can watch videos on the creation of this program from scratch to the result with detailed explanations and independent tasks.
Good luck!
Source: https://habr.com/ru/post/396453/
All Articles