Space-time quantum fabric: tapestry network

How quantum pairs stitch spacetime

First part

Brian Swing studied physics at the Massachusetts Institute of Technology postgraduate when he decided to take a couple of string theory classes to improve his education - as he recalls, according to the "why not" principle - although he didn’t pay attention to the concepts whom he met on this course. But plunging deeper, he began to notice unexpected connections with his own work, in which he used the so-called. tensor networks for predicting the properties of exotic materials and an approach to black hole physics and quantum gravity, taken from string theory. “I realized that something amazing was happening,” he says.
')
Tensors periodically unexpectedly arise in different areas of physics - these are mathematical objects that can represent many numbers at once. For example, the velocity vector is the simplest tensor: it includes both speed and direction. More complex tensors connected in a network can be used to simplify calculations for complex systems made up of many interacting parts — including the intricate interactions of a huge number of subatomic particles that make up matter.

Swing is one of the growing number of physicists who see the value of applying tensor networks to cosmology. Among other benefits, it can help resolve an ongoing debate about the essence of spacetime. John Preskill , professor of Richard Feynman in theoretical physics at Kaltech, believed that many physicists suspected a deep connection between quantum entanglement — the frightening long-range action that had so angered Einstein — and the geometry of space-time on the smallest scales. This has been going on since John Wheeler, 60 years ago, first described spacetime as bubbling foam. “If you study geometry on scales comparable to the Planck ones,” at the shortest possible distances, “it looks less and less like space-time,” says Presquill. "This is generally no longer geometry, but something else, something that arises from more fundamental things."

Physicists continue to struggle with the confusing problem of what this more fundamental problem might be, but they suspect that it is related to quantum information. “When we talk about coding information, we mean that the system can be divided into parts and there will be such a correlation between them that I can learn something about one of the parts by watching the other,” says Presquill. This is the essence of confusion.

Often they speak of the "fabric" of space-time, and this metaphor leads to the concept of stitching individual threads together to form a smooth whole. These threads are essentially quantum. “Entanglement is a fabric of space-time,” says Swing, who is currently working on research at Stanford. - This is a thread that binds the entire system together, ensuring that the general properties are different from the properties of individual entities. But in order to actually see interesting joint behavior, you need to understand how entanglement is distributed. ”

Tensor networks provide a mathematical tool that can do just that. From this point of view, the space-time arises from sets of interconnected nodes of a complex network , where small pieces of quantum information fit together like Lego. Entanglement is the glue that connects the net. In order to understand space-time, it is necessary to begin to consider confusion from geometrical positions, since this is how information is encoded in a huge number of interacting nodes of the system.

Many bodies, one network

Modeling a complex quantum system is not a joke; even a classical system with more than two interacting parts is already quite complex for modeling. When Isaac Newton published his Principia [Mathematical Principles of Natural Philosophy] in 1687, one of the themes of the book was the “three-body problem”. The task of calculating the motion of two objects, for example, the Sun and the Earth, taking into account their mutual attraction, is relatively simple. But if you add a third body to it - for example, the Moon - it turns from a simple problem with an exact solution into a chaotic one, where long-term predictions require powerful computing systems to simulate an approximate evolution of the system. And the more objects in the system, the more difficult the calculations, and their complexity grows almost linearly - at least in classical physics.

Now imagine a quantum system with billions of atoms, each of which interacts with others according to complex quantum equations. On this scale, complexity seems to grow exponentially with an increase in the number of particles in the system, so the approach to computing using brute force simply does not work.

Imagine the golden nugget. It consists of billions of atoms, and they all interact with each other. From these interactions, various classical properties of the metal arise — color, strength, or conductivity. “Atoms are tiny things that obey quantum mechanics, and when you put them together, new and amazing things happen,” says Swing. But on these scales, the rules of quantum mechanics begin to work. Physicists need to accurately calculate the wave function of this nugget, which describes the state of the system. And this function is a multi-headed hydra of exponential complexity.

Even if the nugget has only one hundred atoms and each has a quantum spin that takes one of two states, up or down, the total number of possible states will be already ^2,100 , million trillions. And with the addition of each atom, the problem deteriorates exponentially. (And it turns out even worse when you try to describe anything other than spins, like any realistic model should do). “If you take the entire visible Universe and fill it with the best hard drives available to you, the best hard drives, you can only hold 300 spins on them,” says Swing. - There is information, but not all of it corresponds to physics. No one has ever measured these numbers. ”

Tensor networks allow physicists to compress all the information contained in the wave function and concentrate only on those properties that can be measured in the experiment: how much the material refracts the light, or how well it absorbs sound, or how it conducts electricity. A tensor is a “black box” that takes one set of numbers and gives out another. Therefore, it is possible to connect a simple wave function — for example, sets of electrons not interacting with each other in a state with the lowest energy — and process it with tensors again and again until the process produces a wave function for a large and complex system, such as billions of interacting in gold nugget atoms. The result is a simple diagram representing this complex nugget — an innovation comparable to the diagrams developed by Feynman in the mid-20th century that simplified the representation of particle interactions. And the tensor network has its own geometry, like space-time.

The key to simplification lies in the principle of "locality". Each individual electron interacts only with the nearest electrons. The entanglement of each electron with its neighbors gives a set of "nodes" of the network. These nodes are tensors and entanglement linking them together. All of these interconnected nodes make up the network. Complex calculations are easier to visualize. Sometimes it all comes down to a simpler calculation task.

There are many different types of tensor networks, but among the most useful there is one, known by the acronym MERA (the ansatz of the renormalization of multi-scale entanglement). The principle of its operation is the following: imagine a one-dimensional line of electrons. Replace eight different electrons - denote them by A, B, C, D, E, F, G, and H - by the fundamental units of quantum information (qubits) and entangle each of them with a neighbor to form bonds. A gets confused with B, C with D and so on. This is a higher level network. Then confuse AB from the CD, and EF with GH, to go up another network level. Finally, ABCD gets entangled with EFGH to form the highest level. “In a sense, we can say that entanglement is used to build the wave function of many bodies,” wrote Roman Orus [ Román Orús ] in his work last year, a physicist from the University. Johann Gutenberg (Germany).

Why are some physicists so optimistic about the potential of tensor networks — especially MERA — that can lead them to quantum gravity? Because networks show how a simple geometric structure can emerge from complex interactions between many objects. And Swing with like-minded people hopes that this new geometry can be used by showing how it explains the mechanism for turning individual pieces of quantum information into smooth, continuous space-time.

Borders of space-time

Specialists in condensed matter physics in the development of tensor networks inadvertently discovered an additional dimension: this technique leads to the appearance of two-dimensional systems in one dimension. And experts on the theory of gravity removed one dimension - moving from three to two - by developing the so-called. holographic principle. These two concepts can unite and create a more complex view of space-time.

In the 1970s, physicist Jacob Bekenstein [Jacob Bekenstein] showed that information about the interior of a black hole is encoded on its flat two-dimensional surface (on the border), and not in its three-dimensional volume. Twenty years later, Leonard Susskind and Gerard 't Hooft [Leonard Susskind and Gerard' t Hooft] expanded this concept to the entire Universe, equating it to a hologram: our three-dimensional Universe in all its glory emerges from the two-dimensional "source code." In 1997, Juan Maldacena found a concrete example of how a hologram works by demonstrating that a toy model describing flat space without gravity is equivalent to describing a saddle space with gravity. This interrelation of physics is called “duality”.


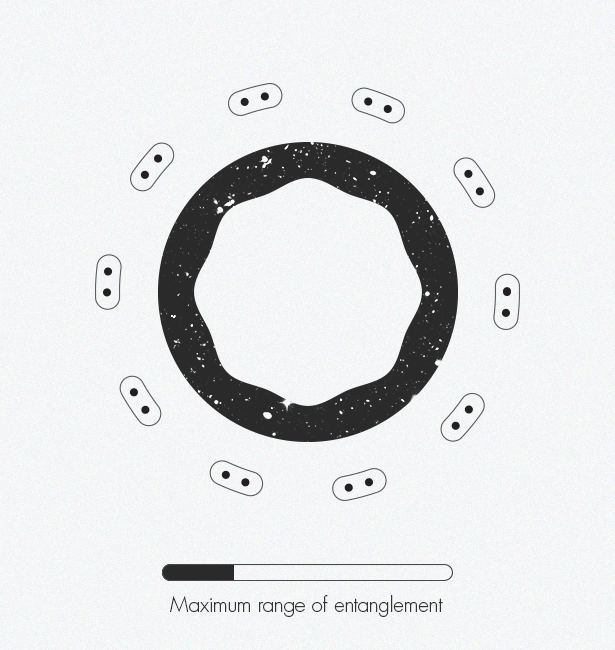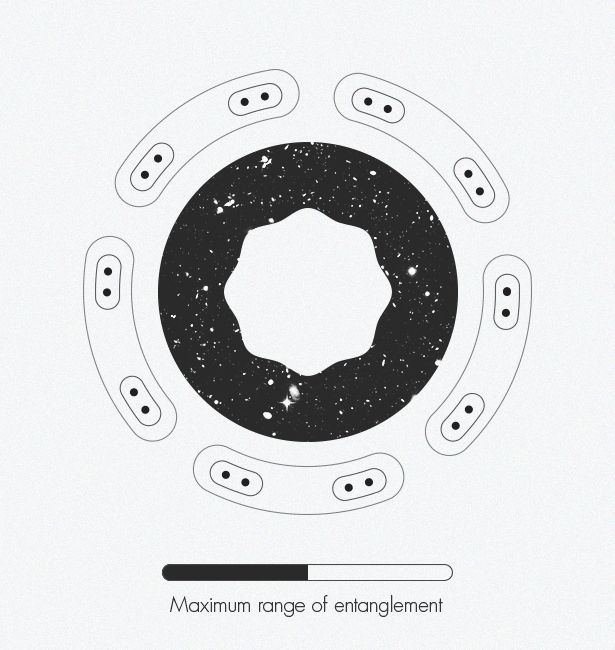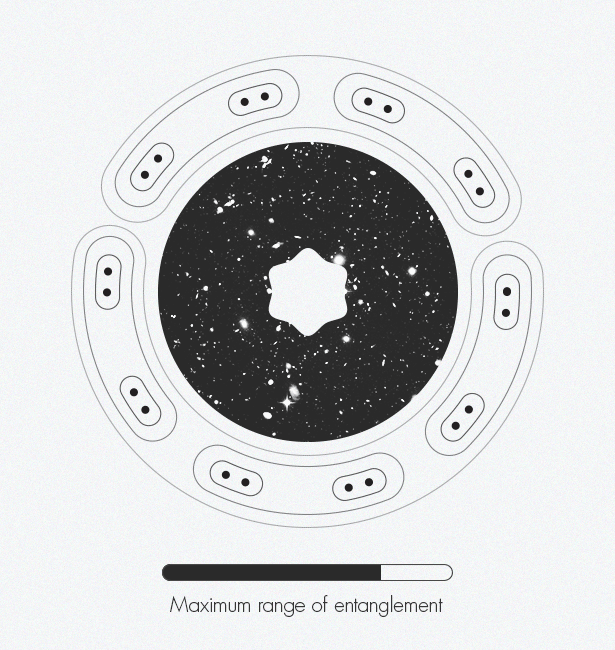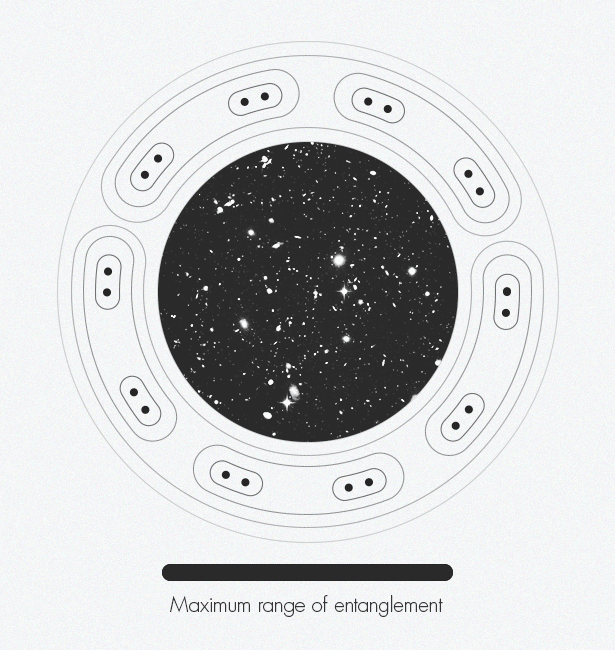
Mark Van Raamsdonk [ Mark Van Raamsdonk ] represents how entanglement gradually creates space-time. Along the edges of the figure, the individual particle-points begin to get entangled with each other. These tangled pairs are tangled with other pairs. As more and more pairs get entangled, the structure of space-time appears.

Mark van Raamsdonk, a string theory specialist at the University of British Columbia (Vancouver), compares this holographic principle with a two-dimensional computer chip containing code for creating a three-dimensional virtual world in a computer game. We live inside the three-dimensional space of the game. In a sense, our space is illusory and is only an ephemeral image hanging in the air. But van Raamsdonk stresses that "there is still some physical entity in the computer that stores all the information."

The idea has received wide recognition among theoretical physicists, but they are still struggling with how exactly smaller dimensions store information about the geometry of space-time. The catch is that our metaphorical computer chip must be a kind of quantum computer, in which the usual zeroes and ones are replaced by qubits, capable of simultaneously representing all possible states from zero to one. These qubits must be entangled - so that the state of one qubit is determined by the state of its neighbor - before the realistic three-dimensional world can be encoded.

Similarly, entanglement looks like a fundamental feature of spacetime. Two scientists came to this conclusion in 2006: Shinsei Ryu (University of Illinois) and Tadashi Takayanagi (University of Kyoto) Tadashi (Kyoto University), who shared the 2015 New Horizons of Physics award. “The idea is that the way space-time geometry is coded is strongly related to how different parts of this chip are entangled with each other,” explains van Raamsdonk.

Inspired by their work, as well as the work of Maldacena that followed, in 2010, van Raamsdonk proposed a mental experiment demonstrating the critical role of entanglement in the formation of space-time. He investigated what would happen if the computer chip was halved and then the entanglement between the qubits in the two halves was removed. He found that space-time begins to collapse just as stretching a piece of gum at the ends leads to a gap in the middle. The division of this chip into smaller and smaller pieces breaks the space of time until only separate, unrelated pieces remain. “If confusion is removed, space-time just falls apart,” says van Raamsdonk. In the same way, “if you want to build space-time, you will have to confuse qubits in a certain way.”

Add these thoughts to the work of Swingl, which connects the intricate structure of space-time and the holographic principle with tensor networks and one more piece of the puzzle falls into place. The curved space-time arises naturally from entanglement in tensor networks through holography. “Spacetime is a geometric representation of this quantum information,” says van Raamsdonk.

And what does this geometry look like? In the case of Maldacena's saddled space-time, it looks like one of Escher’s “limit-circle” drawings from the 1950s and 1960s. Escher has long been interested in order and symmetry, including these mathematical concepts in his works since 1936, when he visited the Alhambra architectural and park ensemble in Spain and found inspiration in the recurring tiled patterns typical of Moorish architecture known as mosaic.

His woodcuts "limit - circle" illustrate hyperbolic geometries: the distortion of space with negative curvature on a two-dimensional disk surface resembles the flattening of a globe to a two-dimensional map of the Earth, distorting the shape of continents. For example, the " limit - circle IV " (hell and heaven) looks like a set of repeating figures of angels and demons. In hyperbolic space, the size of all the figures would be the same, but in Escher’s two-dimensional representations, the figures at the edge look smaller than in the center. The tensor network diagram very much resembles the “limit-circle” series, a visual representation of the deep connections that Swingl found when he attended those same string theory classes.

To date, tensor analysis is limited to space-time modeling (like that of Maldasena), which does not describe the Universe in which we live - it does not have the shape of a saddle, but its expansion is accelerating. Physicists can translate between models only in certain special cases. Ideally, they need a universal "dictionary." And they would like to display this dictionary directly, without using approximations. “With these dualities, we found ourselves in an amusing position, because everyone agrees that they are very important, but no one knows how to deduce them,” says Presquill. “Maybe the approach of tensor networks will make further progress possible. I think a sign of progress would be if we could say, even if in the case of a toy model: 'Aha! Here it is, the conclusion of the dictionary! It would be a serious hint that we stumbled upon something important. ”

Over the past year, Swing and van Raamsdon have worked together to promote their work in the region emerging from a static view of space-time to a dynamic one. They are interested in how space-time changes over time and how it bends in response to these changes. So far, they have managed to derive Einstein's equations, specifically the equivalence principle. This proves that the dynamics of space-time, like its geometry, is based on entangled qubits. The start is promising.

"The question is" What is space-time? " It seems absolutely philosophical, says van Raamsdonk. “In fact, to find an answer to it, specific and allowing to conduct calculations of space-time, that would be amazing.”