Ask Ethan # 78: Why is E = mc2?

Einstein’s most famous equation is calculated more beautifully than one would expect.

From the special theory of relativity it follows that mass and energy are different manifestations of the same thing - a concept unknown to the average mind.
- Albert Einstein

Some scientific concepts are so changing the world and so deep that almost everyone knows about them, even if they do not fully understand. Why not work on it together? Every week you send your questions and suggestions, and this week I chose the question of Mark Liuva who asks:

Einstein derived the equation E = mc ² . But units of energy, mass, time, length were already known before Einstein. So how is it so beautiful? Why is there no constant for length or time? Why is it not E = amc ² , where a is some constant?
')
If our Universe had not been arranged as it is now, then everything could be different. Let's see what I mean.



On the one hand, we have objects with a mass: from galaxies, stars and planets to the smallest molecules, atoms and fundamental particles. Although they are tiny, each of the components of what we know under the name of matter has a fundamental property of mass, which means that even if we exclude its movement, even if we slow it down to a complete stop, it will still affect all the others objects of the universe.



Specifically, it exerts a gravitational pull on everything else in the universe, no matter how far away a distant object is. He attracts everything to himself, experiences attraction to everything else, and also has the energy inherent in his very existence.

The last statement is counterintuitive, because energy, at least in physics, is said to be about how to do something — about the possibility of doing work. And what can you do if you just sit still?

Before answering, let's look at the other side of the coin - things without mass.



On the other hand, there are things that have no mass - for example, light. These particles have a certain energy, and this is easy to understand by observing their interaction with other things — when absorbed, the light transfers their energy to them. Light with sufficient energy can heat matter, add kinetic energy (and speed), knock electrons to upper energy levels or ionize altogether, depending on energy.



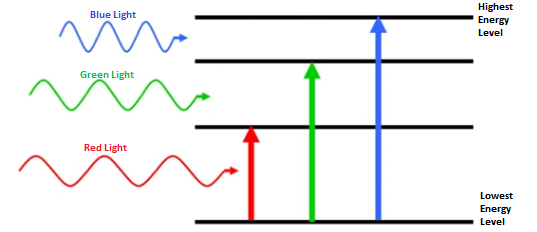
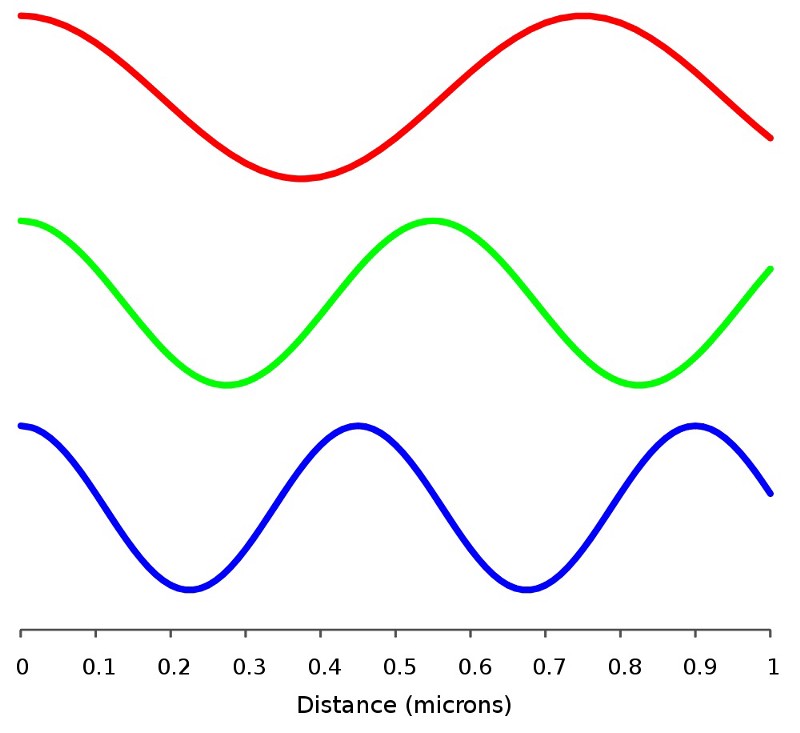
Moreover, the amount of energy contained in a massless particle is determined only by its frequency and wavelength, the product of which is always equal to the velocity of the particle: the speed of light. This means that the longer waves have lower frequencies, and the energy is less, and the short ones have frequencies and energy higher. A massive particle can be slowed down, and attempts to take energy away from the massless will only lead to the elongation of its wave, and not to a change in speed.



With this in mind, let us think how mass-energy can be equivalent to work? Yes, you can take a particle of matter and a particle of antimatter (electron and positron), push them together and get massless particles (two photons). But why are the energies of two photons equal to the masses of an electron and a positron multiplied by the square of the speed of light? Why is there no other factor, why does the equation exactly equate E and mc ² ?



What is interesting, according to SRT, the equation simply must look like E = mc ² , without any deviations. Let's talk about the reasons for this. First, imagine that you have a box in space. It is motionless, and on both sides it has a mirror, and inside is a photon flying to one of the mirrors.



Initially, the box does not move, but since the photons have energy (and momentum) when the photon collides with the mirror on one side of the box and bounces off, the box will move in the direction in which the photon initially moved. When the photon reaches the other side, it will reflect from the mirror on the other side, changing the momentum of the box back to zero. And it will continue to be reflected in this way, while the box will move half the time to one side, and the other half remain motionless.

On average, the box will move and, therefore, since it has mass, it will have a certain kinetic energy due to the energy of the photon. But it is also important to remember about the impulse, the amount of movement of the object. The photon momentum is related to their energy and wavelength is very simple: the shorter the wave and the higher the energy, the higher the momentum.



Let's think about what this means, and for this we will conduct another experiment. Imagine what happens when initially only the photon itself moves. He will have a certain amount of energy and momentum. Both properties must be preserved, so at the initial moment the photon energy is determined by its wavelength, and the box has only rest energy - whatever it is - and the photon has the entire system impulse, and the box has zero momentum.



Then the photon collides with the box and is temporarily absorbed. Impulse and energy must be saved - these are the basic laws of conservation of the Universe. If the photon is absorbed, then there is only one way to save the momentum - the box must move at a certain speed in the same direction in which the photon moved.

It's okay for now. Only now can we ask ourselves what is the energy of the box. It turns out that if we go from our usual formula for kinetic energy, K _E = ½mv ² , we presumably know the mass of the box, and, based on the concept of impulse, its speed. But if we compare the energy of the box with the energy of the photon that it had before the collision, we will see that the energy of the box is not enough.

Problem? No, it's pretty easy to solve. The energy of the box / photon system is equal to the rest mass of the box plus the kinetic energy of the box plus the photon energy. When a box absorbs a photon, most of its energy goes into an increase in box weight. When the box is absorbed by the photon, its mass changes (increases) compared to the one that was before the collision.

When the box again emits a photon in a different direction, it receives an even greater impulse and speed (which is compensated by the negative impulse of the photon in the opposite direction), more kinetic energy (and the photon has energy), but instead loses some rest mass. If you count everything (there are three different ways to do this, and here is a description), you can find that the only mass conversion that allows you to save energy and momentum is E = mc ² .



If you add any constant, the equation will no longer be balanced, and you will lose or acquire energy each time a photon is emitted or absorbed. Having discovered antimatter in the 1930s, we directly saw confirmation that energy can be converted into mass and vice versa, and the results of the transformations exactly coincided with E = mc ² , but it was thought experiments that allowed this formula to be derived several decades before the observations. Only by putting the photon in correspondence with the effective mass, equivalent to m = E / c ² , can we ensure the conservation of energy and momentum. And although we say E = mc ² , for the first time Einstein wrote the formula differently, assigning an energy equivalent mass to massless particles.

So, thank you for the wonderful question, Mark, and I hope that this thought experiment will help you understand why we need not only the equivalence of mass and energy, but also why this equation has only one possible value for a “constant” that will help preserve energy and impulse - and this is demanded by our Universe. The only equation that works is E = mc ² . Send me your questions and suggestions for the following articles.