Electromagnetism for the smallest, and not only
If we talk about Maxwell's “electromagnetism,” then the people as a whole are divided into two groups: the first believe that they know enough about this topic if not all. Because there is nothing difficult there. The latter do not quite know this topic and do not want to know. Since incomprehensible formulas and in general.
Bumping into different places on how some points are explained: on the one hand it is convincing, on the other it is doubtful, on the third it is wrong, on the fourth, in principle and true ... I think it’s worth a look at them just in case, then the "smallest" can rise without fear of formulas.
First of all, we will be interested in how electromagnetic waves are generated and propagated from “electric” and “magnetic” fields, and therefore immediately a litmus test:

')
If this scheme is perfectly familiar to you and does not cause a reflex to clarify and supplement something so that it does not mislead others, then I ask for a cat. If you are perfectly familiar with it, and you understand that it is necessary to clarify it, then walk further) Fasting is not for you.
If the scheme is not very familiar or clear, you can look.
To go in order, let's start from far away, namely, let's take and consider a circle . It would seem that what is there to say, the figures are no easier. Since childhood, we used to draw, taking the center point on paper and outlining all the points at the same distance from the center.
Then we will learn other ways to draw a circle. It would seem that very different principles, and lead to one and the same.
Take one of them, one of the most useful in my opinion:
What was it? Nothing but the differential equation of a circle. The meaning of which is:
“There are two interacting entities. The first one applies forces to strengthen the second. The second, as far as possible, is trying to weaken the first. ”
We can write this dynamics in the form of the simplest system diff. equations in the world (not counting exponentials)

Figuratively speaking, at any moment of a very short period of the same length "dt", the change in "y" (ie, "dy") depends on the value of "x".
At the same time, the change in “x” (i.e., “dx”) depends on the value of “y”.
Both equations are similar to the macroscale mechanics equation - “distance = speed * time”. Only in this case the “dt” segments are very small (or rather, infinitely small, but do not change the essence).
Moreover, all these dependencies are linear, and they know nothing about the circle. And the principle of yin-yang is manifested in the opposing signs of the influence of one element on another.
If the system is out of balance, i.e. “X” and “y” are not equal to zero; this interaction, adding all the micro-lengths of time, will lead to an infinite cycle of oscillations.
— , .. «» «» ( ).
, — , — … . …
«x» «y» ( ) , /2

, .
. 3- . , , , .
, ( ). ( ).
«E» ( ) «B» ( )

( « », )
, , .. . . -. — «E», «B» «t», , «J» , , .
, «», «B», , . .
— «» «B», .. «» . - . , , .
, , , , /2.
, . , , (=), , … .. ( ) , .
… :

… ? , , !
? . . ? . ?
- … ? . « , ». «», . , ? , 300 , - ?
: www.sciforums.com/threads/luminiferous-ether.57402
, , . .
? , .
? !
«» . , 3 ( ).
, . , .
, , «». , , , .

, , .
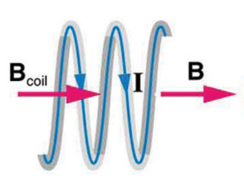
, ( ), , — .
?
…

, , .. , . , .. , .
… /2 .
? … - . , - (). ?
, - , .. .
… ? ?
Bumping into different places on how some points are explained: on the one hand it is convincing, on the other it is doubtful, on the third it is wrong, on the fourth, in principle and true ... I think it’s worth a look at them just in case, then the "smallest" can rise without fear of formulas.
First of all, we will be interested in how electromagnetic waves are generated and propagated from “electric” and “magnetic” fields, and therefore immediately a litmus test:

')
If this scheme is perfectly familiar to you and does not cause a reflex to clarify and supplement something so that it does not mislead others, then I ask for a cat. If you are perfectly familiar with it, and you understand that it is necessary to clarify it, then walk further) Fasting is not for you.
If the scheme is not very familiar or clear, you can look.
To go in order, let's start from far away, namely, let's take and consider a circle . It would seem that what is there to say, the figures are no easier. Since childhood, we used to draw, taking the center point on paper and outlining all the points at the same distance from the center.
Then we will learn other ways to draw a circle. It would seem that very different principles, and lead to one and the same.
Take one of them, one of the most useful in my opinion:
Secret of the universe

What was it? Nothing but the differential equation of a circle. The meaning of which is:
“There are two interacting entities. The first one applies forces to strengthen the second. The second, as far as possible, is trying to weaken the first. ”
We can write this dynamics in the form of the simplest system diff. equations in the world (not counting exponentials)

Figuratively speaking, at any moment of a very short period of the same length "dt", the change in "y" (ie, "dy") depends on the value of "x".
At the same time, the change in “x” (i.e., “dx”) depends on the value of “y”.
Both equations are similar to the macroscale mechanics equation - “distance = speed * time”. Only in this case the “dt” segments are very small (or rather, infinitely small, but do not change the essence).
note about the record
Normally diff. ur write to demonstrate the differential, in this case, the time derivative, therefore a typical entry:


Moreover, all these dependencies are linear, and they know nothing about the circle. And the principle of yin-yang is manifested in the opposing signs of the influence of one element on another.
If the system is out of balance, i.e. “X” and “y” are not equal to zero; this interaction, adding all the micro-lengths of time, will lead to an infinite cycle of oscillations.
Html code for example
<html>
<body>
<canvas height='300' width='300' id='cnv' style="border: 1px solid black"></canvas>
<canvas height='300' width='200' id='cnv2' style="border: 1px solid black"></canvas>
<script>
var cnv = document.getElementById("cnv");
var cx = cnv.getContext('2d');
var cnv2 = document.getElementById("cnv2");
var cx2 = cnv2.getContext('2d');
var h = parseInt(cnv.getAttribute("height"));
var w = parseInt(cnv.getAttribute("width"));
var h2 = parseInt(cnv2.getAttribute("height"));
var w2 = parseInt(cnv2.getAttribute("width"));
var id = cx.createImageData(w, h);
var id2 = cx2.createImageData(w2, h);
var rd = Math.round;
var x = 0, y = 1, x1, y1;
var dt = 0.0001;
var t=0;
i=1000000; while (i--) {
dx = -y;
dy = x;
x1 = x + dx*dt;
y1 = y + dy*dt;
t = t + dt;
x = x1; y = y1;
// draw (x, y)
drawOn(id, rd(100*x + 150), rd(100*y + 150), w, h, 0, 0, 0);
// draw x(t), y(t)
drawOn(id2, rd(10*t), rd(100*y + 150), w2, h2, 255, 0, 0);
drawOn(id2, rd(10*t), rd(100*x + 150), w2, h2, 0, 0, 255);
}
drawHorizLine(id, 0, w, h/2, w, h);
drawHorizLine(id2, 0, w2, h2/2, w2, h2);
cx.putImageData(id, 0, 0);
cx2.putImageData(id2, 0, 0);
function drawOn(id, x, y, w, h, red, green, blue) {
if (x < w && y < h && x >=0 && y >=0) {
var idx = 4*(x + y*w);
id.data[idx] = red;
id.data[idx+1] = green;
id.data[idx+2] = blue;
id.data[idx+3] = 255;
}
}
function drawHorizLine(id, xFrom, xTo, y, w, h) {
for (var x = xFrom; x < xTo; x++) {
drawOn(id, x, y, w, h, 0, 0, 0);
}
}
</script>
</body>
</html>
— , .. «» «» ( ).
, — , — … . …
«x» «y» ( ) , /2

, .
. 3- . , , , .
, ( ). ( ).
«E» ( ) «B» ( )

( « », )
, , .. . . -. — «E», «B» «t», , «J» , , .
, «», «B», , . .
— «» «B», .. «» . - . , , .
, , , , /2.
, . , , (=), , … .. ( ) , .
… :

… ? , , !
? . . ? . ?
- … ? . « , ». «», . , ? , 300 , - ?
: www.sciforums.com/threads/luminiferous-ether.57402
Hi BillyT,
From my understanding Vern is correct. Your citation of Maxwell's equation is a good idea, but you are incomplete. In free space you have no currents and no charges so Maxwell's 4 equations simplify down to 2 equations (considering a single spatial dimension):
dE/dx = -dB/dt
dE/dt = -c2 dB/dx
So when the temporal derivative of one is maximal the spatial derivative of the other is minimal (maximally negative). If you consider a simple single-frequency sinusoidal plane wave you find that this happens for E and B in phase. In the above equations:
E = Emax cos(kx-wt)
B = Bmax cos(kx-wt)
, , . .
? , .
? !
dE/dx — .«» . , 3 ( ).
, . , .
, , «». , , , .

, , .

, ( ), , — .
?
…

, , .. , . , .. , .
… /2 .
? … - . , - (). ?
, - , .. .
… ? ?
Source: https://habr.com/ru/post/390731/
All Articles