Expert opinion: Magnetic nanoparticles: theory and modern technological applications
As we wrote earlier, the “Christmas Lectures” event is held annually at NUST “MISiS ” . In the framework of this event, our leading scientists give a lecture on their scientific fields and major achievements. We have already published the expert opinion of D.V. Golberg on lecture.
Today we would like to publish the expert opinion of our leading scientist, project manager for the “Development and application of amorphous ferromagnetic microwires for the creation of new sensors, composite materials and devices based on them” Dr.Sc. Professor Nikolai Aleksandrovich Usov .
His lecture “Modern magnetism in applications: magnetic recording, biomedicine, microelectronics” was held on December 3 and made a vivid impression on all the listeners, and many research workers noted its pedantry in the preparation of the material. Our directorial team edited a very good video for that lecture, by the way, it lasted the longest. We could not help asking the professor to write an expert opinion for us. As always, Nikolai Aleksandrovich very responsibly approached the task and two months later sent us material. Of course, this is not a popular science format, and its comprehension will require a university level of knowledge of physics.
In his expert opinion, the professor will talk about magnetic nanoparticles and their modern technological applications.

Ensembles of magnetic nanoparticles are widely used in modern nanotechnology. Suffice it to mention such important applications of magnetic nanoparticles as super-dense magnetic information recording, magnetic fluids with unique rheological properties, high-coercive permanent magnets, etc. Recently, very promising biomedical applications of magnetic nanoparticles, such as magnetic resonance imaging, targeted drug delivery, magnetic hyperthermia, deep purification of biological media from toxins and impurities, etc. d.
')
Chemists, physicists, engineers and technologists have been working with various ensembles of magnetic nanoparticles for many years, seeking to optimize the physicochemical properties of ensembles for various technical applications. This work is far from complete. This is due, firstly, to the fact that the very phenomenon of magnetism is quite difficult to study. And secondly, it is very difficult to work with nano-objects, which can only be observed with the help of perfect electron microscopes.
Ferromagnetic substance has a special magnetic order, which is absent in ordinary substances. Namely, at each point of the ferromagnetic body there is a magnetization vector M®, the length of which is constant and equal to a physical quantity, called the saturation magnetization of the substance, | M® | = Ms. The saturation magnetization is the number of elementary magnetic moments per unit volume of a ferromagnetic substance, whose behavior is correlated by quantum-mechanical exchange interaction [1, 2]. The main subject of study in ferromagnetism is the analysis of the possible types of distribution of the M® vector over the volume of the ferromagnetic body, depending on the applied magnetic field and other factors. It turns out that the vector M® cannot change abruptly, irregularly, but can only unfold smoothly in a magnetized body from point to point, while maintaining its length. Thus, in essence, magnetism is a three-dimensional vector field.
Note that we live surrounded by various physical fields. For example, the non-uniform temperature distribution inside and around us has a three-dimensional scalar temperature field. This field is described by a single function T (r, t), which can depend not only on the position of a point in the space r, but also on the time t. To describe the vector field, we need three functions — the projections of this vector on the axis of the Cartesian coordinate system, {Mx (r, t), My (r, t), Mz (r, t)}. The essential property of a magnetic vector that radically distinguishes the field of this vector from other physical fields is the constancy of the length of the magnetic vector, Mx2 (r, t) + My2 (r, t) + Mz2 (r, t) = Ms2, which is dictated by the laws of quantum mechanics [ 1.2]. This relationship is non-linear, since it connects the squares of the quantities. Therefore, the study of ferromagnetism requires the use of special nonlinear mathematics, which is much more complicated than ordinary mathematical analysis. In addition, any magnetized body creates inside and around itself a distribution of the magnetic field, H®, which itself affects the distribution of magnetization in the ferromagnetic body. With distance from the magnetized body, the H® field decreases in space slowly, in proportion to ~ 1 / r3, that is, it is long-range. This means that even sufficiently distant parts of the magnetized body are connected by magnetic interaction, that is, their behavior is consistent.
These two circumstances — the nonlinearity of the equations, which describe the distribution of the M® vector in space, and the long-range nature of the magnetic interaction, make it extremely difficult to theoretically analyze the properties of ferromagnetic materials. Although the basic equations of phenomenological ferromagnetism were formulated by Landau and Lifshitz a long time ago, in their famous work in 1935 [3], significant progress was made in developing the theory of ferromagnetism only in the 90s of the last century, due to the development of powerful computer modeling methods. Until now, magnetic nanoparticles remain one of the central objects of the theory of ferromagnetism, and are still an important area of experimental research. The fact is that an extended ferromagnetic body has a large number of magnetic degrees of freedom. Indeed, in a macroscopically large body, the vector M® can unfold in space in a huge number of ways. This phenomenon is said to be about the presence of a large number of stable distributions of magnetization, which can also easily transform into each other. Therefore, the properties of an extended ferromagnet are difficult to control, since it is difficult to fix the magnetic state of such a body.
It is clear, however, that the number of magnetic degrees of freedom decreases sharply with decreasing volume of the body. Indeed, the quantum mechanical exchange interaction allows only fairly smooth changes of the M® vector in space, at characteristic lengths exceeding the so-called Lex exchange length. In good ferromagnets, such as iron, cobalt, nickel and their alloys, the exchange length is in the order of magnitude 20-30 nanometers. If the characteristic size of the nanoparticle D is less than or of the order of the exchange length, D <Lex, then the rotation of the magnetization vector within such a particle is energetically unfavorable. More strictly speaking about the characteristic size of a single domain, Dc, [4] which in the so-called magnetically soft ferromagnets is close to the exchange length, Dc ~ Lex. Particles with sizes smaller than the single-domain diameter, D <Dc, are magnetized uniformly, that is, their magnetization vector does not depend on the coordinates, M = const. Such particles with the simplest magnetic structure are called single-domain. A single-domain particle is a small permanent natural magnet, which is almost impossible to demagnetize. If the particle size exceeds the size of the single-domain state, D> Dc, then inhomogeneous magnetization distributions, as a rule, of the vortex type, can develop in such a particle.

In Fig. Figure 1 shows the homogeneous and vortex magnetization distributions calculated by modern numerical methods [5] in spherical cobalt nanoparticles of different diameters. Three-dimensional distributions of the magnetization vector in these particles are represented in these figures by arrows of fixed length. To determine the single-domain diameter of a spherical cobalt nanoparticle, it is necessary to count the energy diagram of these states, schematically shown in Fig. 2
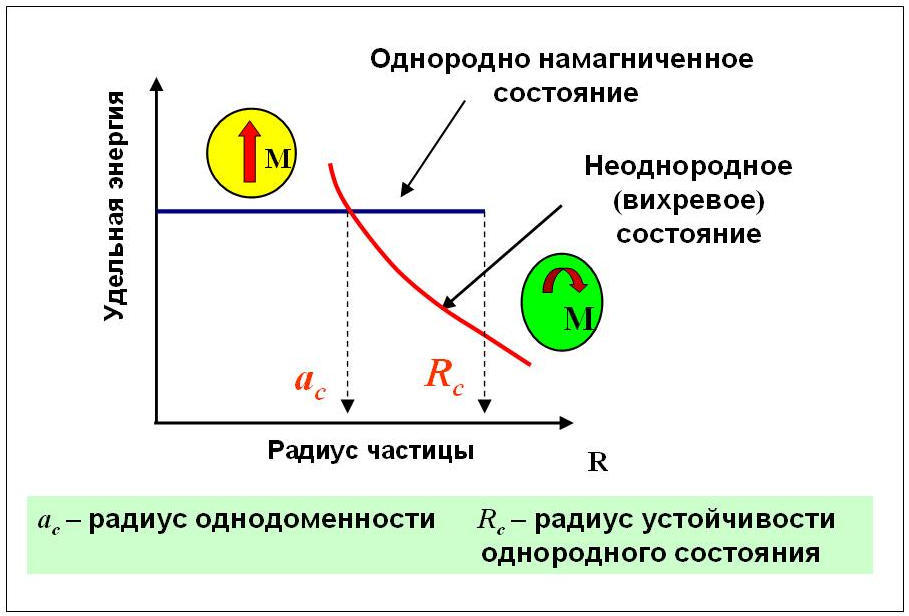
As can be seen from Fig. 2, the total specific energy of a uniformly magnetized state of a particle (black line) does not depend on the radius of the particle, while the total energy of the vortex state (red curve) decreases rapidly with increasing its radius. The intersection point of these curves determines the single-domain radius of the particle ac = Dc / 2. If the particle radius is r <ac, then the homogeneous state has the lowest total energy, while the vortex state in a certain region of the radii can exist as metastable, that is, it can be stable, but it can have more energy. If r> ac, then the lowest energy vortex state will be. In this case, a homogeneous state can exist as a metastable in the range of radii ac <r <Rc, where Rc is the radius of stability of the homogeneous state.
For most technical applications, it is convenient to work with an ensemble of single-domain nanoparticles, whose properties can be relatively accurately predicted and controlled. A single-domain nanoparticle in all circumstances retains its full magnetic moment, while the average magnetic moment of a particle in the vortex state may be small, since the magnetic vectors in this state close themselves to themselves. For a particle in the vortex state, the average value of the magnetic moment substantially depends on the magnitude of the external magnetic field acting on the particle. From the diagram Fig. 2 shows that if the ensemble has a variation of nanoparticles in size near the single-domain radius, then in fact such an ensemble is an uncontrollable mixture of particles with different properties, single-domain and non-single-domain. If we also take into account that the value of the single-domain radius depends on the shape of the particle (sphere, elongated or oblate spheroid), then the experimental situation becomes quite confusing.
We see that an ensemble of magnetic nanoparticles is a rather complex physical system, the properties of which are determined by many different factors. In most cases (although not always) the ensemble consists of nanoparticles of the same chemical composition. Consequently, the ensemble particles can be characterized by a single set of material magnetic parameters, that is, the saturation magnetization Ms, the type of magnetic anisotropy and the value of the magnetic anisotropy constant K. The magnetic anisotropy determines the selected directions (the so-called light axes) in space with respect to the axes of symmetry of the crystal. In the absence of an external magnetic field, the particle magnetization vector spontaneously orients along the easy axes of the magnetic crystal. But the assignment of magnetic parameters alone is completely insufficient for the complete characterization of an ensemble of nanoparticles. It is necessary to know the distribution of nanoparticles in size and shape; the number and orientation of the light axes of nanoparticle anisotropy (oriented or non-oriented ensemble); distribution of nanoparticle centers in space. For example, the centers of nanoparticles can be located periodically, forming a certain spatial lattice, or occupy random positions, with some average distance between the particles.
Note that in real experiments, as a rule, fairly dense ensembles of particles are studied, whose properties differ significantly from the properties of rare ensembles. A theoretical study of the properties of a dense ensemble of particles is complicated by the long-range nature of the magnetic dipole interaction between the particles of the ensemble. Therefore, for an ensemble in which there are Np particles, it is necessary to take into account the Np2 pair interactions of the particles, so that the computational complexity quickly increases with the number of particles in the ensemble.
Further, the properties of the ensemble are significantly influenced by the environment in which the ensemble is located. It is necessary to distinguish mediums of relatively low viscosity, in which particles of an ensemble under the influence of an external magnetic field or magnetic dipole interaction of neighboring particles can be rotated as a whole, and media such as a solid matrix, in which rotation of nanoparticles as a whole is impossible. Finally, the ambient temperature can significantly affect the properties of an ensemble of particles of sufficiently small size (superparamagnetic nanoparticles). If the temperature of the medium exceeds the so-called blocking temperature of the magnetic moments of the nanoparticles, then the temperature fluctuations of the magnetic moments of individual particles significantly reduce the average magnetic moment of the ensemble.
Let us turn to the technical applications. The magnetic moment of a single-domain magnetic nanoparticle with uniaxial magnetic anisotropy has two distinct directions in space. At a sufficiently low (for example, room) temperature, in each of these two magnetic states the particle can be indefinitely long. Thus, it retains the memory of the acquired magnetic state, which means that it can store information without loss for quite a long time. If we conditionally assign the value “0” to the direction of the magnetic moment of the particle up, and the value “1” to the direction of the magnetic moment down, as shown in Fig. 3 on the left, then some binary text from a sequence of zeros and ones can be stored in a specially prepared magnetic state of the nanoparticle ensemble. Currently, in the process of magnetic recording, one bit of information is recorded not on one, but on a whole set of 20-40 closely spaced magnetic nanoparticles. The transition to the recording by the principle of “one bit - one particle” would significantly increase the density of magnetic information recording.
Clearly, however, significant technical difficulties that must be overcome to implement this interesting idea. First, the particles of the ensemble should be substantially the same and periodically located in a plane, with a lattice period, of the order of the size of the nanoparticle. It is all the more surprising that chemists have recently learned how to create similar, almost ideally periodic structures of magnetic nanoparticles using self-assembly processes, that is, self-organization of particles in an ensemble during their growth during a chemical reaction (see Fig. 3, right).

However, to implement the idea of super dense recording of information, besides the realization of the correct geometric structure of the ensemble, it is necessary to ensure a sufficiently large value of the magnetic anisotropy constant of the synthesized nanoparticles. In principle, FePt particles with the correct crystal structure, in which the planes of iron atoms alternate regularly with the planes of platinum atoms, have a record high magnetic anisotropy constant, K = 5 * 107 erg / cm3, [7] This allows maintaining the stability of the magnetic state of the particle time and for particles of sufficiently small diameter.
Indeed, to transfer the magnetic moment of a particle between two directions of easy magnetization, it is necessary to overcome the energy barrier of height where V is the volume of the nanoparticle. To prevent spontaneous moment transfer due to thermal fluctuations for a sufficiently long time (10 years), the hard condition KV> (50 - 70) kBT must be met, [7] where T is the ambient temperature, kB is the Boltzmann constant. With a decrease in the particle diameter, the energy barrier rapidly decreases, but the large value of the magnetic anisotropy constant of the particle makes it possible to maintain the indicated inequality for particles of nanometer size. Unfortunately, the FePt particles grown by self-assembly [6] are in a time-oriented magnetic state, when the iron and platinum atoms occupy arbitrary positions in the crystal lattice. And in this case, the constant of magnetic anisotropy of the substance is small, several orders of magnitude less than the specified passport value. Despite significant efforts to convert FePt particles to an ordered magnetic state using annealing and other methods, this fundamental problem has not yet been solved. In general, the problem of the influence of temperature fluctuations of their magnetic moments on the magnetic state of small particles is known as the superparamagnetic limit [7], and is still waiting to be resolved.
where V is the volume of the nanoparticle. To prevent spontaneous moment transfer due to thermal fluctuations for a sufficiently long time (10 years), the hard condition KV> (50 - 70) kBT must be met, [7] where T is the ambient temperature, kB is the Boltzmann constant. With a decrease in the particle diameter, the energy barrier rapidly decreases, but the large value of the magnetic anisotropy constant of the particle makes it possible to maintain the indicated inequality for particles of nanometer size. Unfortunately, the FePt particles grown by self-assembly [6] are in a time-oriented magnetic state, when the iron and platinum atoms occupy arbitrary positions in the crystal lattice. And in this case, the constant of magnetic anisotropy of the substance is small, several orders of magnitude less than the specified passport value. Despite significant efforts to convert FePt particles to an ordered magnetic state using annealing and other methods, this fundamental problem has not yet been solved. In general, the problem of the influence of temperature fluctuations of their magnetic moments on the magnetic state of small particles is known as the superparamagnetic limit [7], and is still waiting to be resolved.
So, the temperature fluctuations of the magnetic moments of the particles lead to considerable difficulties in creating magnetic carriers for superdense recording of information. At the same time, they prove to be very useful for the development of one of the interesting biomedical applications of magnetic nanoparticles, namely, the method of magnetic hyperthermia, intended for the treatment of dangerous oncological diseases. It was experimentally proved [8] that maintaining the temperature of the affected organ is about 42 ° C for 20 to 30 minutes. leads to necrosis of cancer cells, more susceptible to elevated temperature than normal tissue. Many ferromagnetic materials are able to absorb the energy of an external alternating magnetic field and thereby heat the surrounding tissue. However, magnetic nanoparticles have significant advantages for magnetic hyperthermia, because: a) ensembles of superparamagnetic nanoparticles are capable of providing extremely large values of specific energy absorption, of the order of 1 kW per gram of substance; b) due to their small size, nanoparticles can penetrate deeply into biological materials; c) iron oxide nanoparticles are non-toxic, or slightly toxic, for a living organism, d) they have short periods of elimination from the body.
As we saw above, a magnetic nanoparticle is a very strong natural magnet, since the characteristic magnetic reversal field of even a magnetically soft particle of iron oxide at room temperature is quite large, Hc (0) ~ 2K / Ms ~ 400 E. It is important, however, that barrier separating magnetic potential wells, decreases with decreasing volume of the particle, V ~ R3, and can be compared with the characteristic thermal energy kBT. In this case, due to thermal fluctuations of the magnetic moment, the particle loses its average constant magnetization, becoming superparamagnetic. The characteristic residence time of the magnetic moment in a given potential well (Neel relaxation time) is estimated as
decreases with decreasing volume of the particle, V ~ R3, and can be compared with the characteristic thermal energy kBT. In this case, due to thermal fluctuations of the magnetic moment, the particle loses its average constant magnetization, becoming superparamagnetic. The characteristic residence time of the magnetic moment in a given potential well (Neel relaxation time) is estimated as 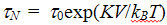 where is a constant
where is a constant  [9]. The relaxation time decreases exponentially rapidly with decreasing particle diameter. Once
[9]. The relaxation time decreases exponentially rapidly with decreasing particle diameter. Once 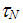 becomes of the order or less than the characteristic time of measurement of the magnetic moment
becomes of the order or less than the characteristic time of measurement of the magnetic moment  , the average magnetic moment of the particle is equal to zero.
, the average magnetic moment of the particle is equal to zero.
But the phenomenon of superparamagnetism has a positive side. Thermal fluctuations, swinging the magnetic moment of the particles in the potential well, effectively lower the energy barrier and significantly reduce the magnitude of the particle magnetization reversal field. Therefore, an ensemble of superparamagnetic particles is able to magnetize in an external alternating magnetic field of moderate amplitude, H0 ~ 100 - 200 Oe, which is extremely important for magnetic hyperthermia, since it simplifies the conditions for creating an alternating magnetic field and reduces the cost of the necessary equipment.
As is known from thermodynamics [1,2], the intensity of the absorption of the energy of an alternating magnetic field is proportional to the area of the hysteresis loop of an ensemble of magnetic nanoparticles. In our group, theoretical calculations were carried out of low-frequency hysteresis loops of sparse ensembles of magnetic nanoparticles of various types [10, 11], as well as the corresponding experimental measurements performed by the original method [12, 13]. Theoretical calculations showed a significant dependence of the hysteresis loops on the frequency of the alternating magnetic field, as shown in Fig. four.
Theoretical analysis shows [10] (see Fig. 5) that the hysteresis loops of a superparamagnetic ensemble also very strongly depend on the average particle diameter, if the particles are fixed in the surrounding nonmagnetic medium. This important fact was confirmed in a number of recent experiments, although at the same time a significant dependence of specific energy absorption on a number of other factors was demonstrated, such as the influence of the magnetic dipole interaction in dense assemblies of magnetic nanoparticles [12, 13].
Magnetic hyperthermia, being a local and distant effect, apparently, does not have such serious side effects as chemotherapy or radiotherapy [8]. It seems that the successful development of magnetic hyperthermia will depend on the successful solution of several problems. First of all, it is necessary to improve the methods of preparation of nanoparticle ensembles with a sufficiently large specific energy absorption in a variable magnetic field of moderate amplitude. This will reduce the dose of nanoparticles, sufficient to achieve a positive therapeutic effect. Ideally, it would be desirable to learn how to locally heat small volumes of tissue in order to suppress small, very dangerous neoplasms at an early stage. Further, it is necessary to ensure the creation of an alternating magnetic field of sufficient amplitude, with the necessary spatial distribution in a given area of the body, at reasonable energy costs, guaranteed safety from electric shock, of moderate cost. Finally, it is necessary to learn how to control the exposure itself, selecting the amplitude and frequency of the magnetic field, the magnetic and geometric parameters of the nanoparticles, the time and frequency of exposure, taking into account the electrodynamic and thermal parameters of the medium. It is also highly desirable to control the spatial and temporal distribution of temperature in the area of impact. Currently, these problems are in the center of attention of researchers in various fields.
Today we would like to publish the expert opinion of our leading scientist, project manager for the “Development and application of amorphous ferromagnetic microwires for the creation of new sensors, composite materials and devices based on them” Dr.Sc. Professor Nikolai Aleksandrovich Usov .
His lecture “Modern magnetism in applications: magnetic recording, biomedicine, microelectronics” was held on December 3 and made a vivid impression on all the listeners, and many research workers noted its pedantry in the preparation of the material. Our directorial team edited a very good video for that lecture, by the way, it lasted the longest. We could not help asking the professor to write an expert opinion for us. As always, Nikolai Aleksandrovich very responsibly approached the task and two months later sent us material. Of course, this is not a popular science format, and its comprehension will require a university level of knowledge of physics.
In his expert opinion, the professor will talk about magnetic nanoparticles and their modern technological applications.

The micrograph shows magnetic needle nanoparticles of chromium dioxide (CrO2) obtained by the method of hydrothermal synthesis in the presence of small modifying additives of tin (Sn) and antimony (Sb).
The particles are collected in the form of eggs, due to their high magnetic characteristics. This material can be used in magnetic recording devices and spin electronics.
Ensembles of magnetic nanoparticles are widely used in modern nanotechnology. Suffice it to mention such important applications of magnetic nanoparticles as super-dense magnetic information recording, magnetic fluids with unique rheological properties, high-coercive permanent magnets, etc. Recently, very promising biomedical applications of magnetic nanoparticles, such as magnetic resonance imaging, targeted drug delivery, magnetic hyperthermia, deep purification of biological media from toxins and impurities, etc. d.
')
Chemists, physicists, engineers and technologists have been working with various ensembles of magnetic nanoparticles for many years, seeking to optimize the physicochemical properties of ensembles for various technical applications. This work is far from complete. This is due, firstly, to the fact that the very phenomenon of magnetism is quite difficult to study. And secondly, it is very difficult to work with nano-objects, which can only be observed with the help of perfect electron microscopes.
Ferromagnetic substance has a special magnetic order, which is absent in ordinary substances. Namely, at each point of the ferromagnetic body there is a magnetization vector M®, the length of which is constant and equal to a physical quantity, called the saturation magnetization of the substance, | M® | = Ms. The saturation magnetization is the number of elementary magnetic moments per unit volume of a ferromagnetic substance, whose behavior is correlated by quantum-mechanical exchange interaction [1, 2]. The main subject of study in ferromagnetism is the analysis of the possible types of distribution of the M® vector over the volume of the ferromagnetic body, depending on the applied magnetic field and other factors. It turns out that the vector M® cannot change abruptly, irregularly, but can only unfold smoothly in a magnetized body from point to point, while maintaining its length. Thus, in essence, magnetism is a three-dimensional vector field.
Note that we live surrounded by various physical fields. For example, the non-uniform temperature distribution inside and around us has a three-dimensional scalar temperature field. This field is described by a single function T (r, t), which can depend not only on the position of a point in the space r, but also on the time t. To describe the vector field, we need three functions — the projections of this vector on the axis of the Cartesian coordinate system, {Mx (r, t), My (r, t), Mz (r, t)}. The essential property of a magnetic vector that radically distinguishes the field of this vector from other physical fields is the constancy of the length of the magnetic vector, Mx2 (r, t) + My2 (r, t) + Mz2 (r, t) = Ms2, which is dictated by the laws of quantum mechanics [ 1.2]. This relationship is non-linear, since it connects the squares of the quantities. Therefore, the study of ferromagnetism requires the use of special nonlinear mathematics, which is much more complicated than ordinary mathematical analysis. In addition, any magnetized body creates inside and around itself a distribution of the magnetic field, H®, which itself affects the distribution of magnetization in the ferromagnetic body. With distance from the magnetized body, the H® field decreases in space slowly, in proportion to ~ 1 / r3, that is, it is long-range. This means that even sufficiently distant parts of the magnetized body are connected by magnetic interaction, that is, their behavior is consistent.
These two circumstances — the nonlinearity of the equations, which describe the distribution of the M® vector in space, and the long-range nature of the magnetic interaction, make it extremely difficult to theoretically analyze the properties of ferromagnetic materials. Although the basic equations of phenomenological ferromagnetism were formulated by Landau and Lifshitz a long time ago, in their famous work in 1935 [3], significant progress was made in developing the theory of ferromagnetism only in the 90s of the last century, due to the development of powerful computer modeling methods. Until now, magnetic nanoparticles remain one of the central objects of the theory of ferromagnetism, and are still an important area of experimental research. The fact is that an extended ferromagnetic body has a large number of magnetic degrees of freedom. Indeed, in a macroscopically large body, the vector M® can unfold in space in a huge number of ways. This phenomenon is said to be about the presence of a large number of stable distributions of magnetization, which can also easily transform into each other. Therefore, the properties of an extended ferromagnet are difficult to control, since it is difficult to fix the magnetic state of such a body.
It is clear, however, that the number of magnetic degrees of freedom decreases sharply with decreasing volume of the body. Indeed, the quantum mechanical exchange interaction allows only fairly smooth changes of the M® vector in space, at characteristic lengths exceeding the so-called Lex exchange length. In good ferromagnets, such as iron, cobalt, nickel and their alloys, the exchange length is in the order of magnitude 20-30 nanometers. If the characteristic size of the nanoparticle D is less than or of the order of the exchange length, D <Lex, then the rotation of the magnetization vector within such a particle is energetically unfavorable. More strictly speaking about the characteristic size of a single domain, Dc, [4] which in the so-called magnetically soft ferromagnets is close to the exchange length, Dc ~ Lex. Particles with sizes smaller than the single-domain diameter, D <Dc, are magnetized uniformly, that is, their magnetization vector does not depend on the coordinates, M = const. Such particles with the simplest magnetic structure are called single-domain. A single-domain particle is a small permanent natural magnet, which is almost impossible to demagnetize. If the particle size exceeds the size of the single-domain state, D> Dc, then inhomogeneous magnetization distributions, as a rule, of the vortex type, can develop in such a particle.

Fig. 1. The state of uniform magnetization in a spherical cobalt nanoparticle with a diameter of D = 36 nm (left) and an inhomogeneous vortex state in the same nanoparticle with a diameter of D = 56 nm (right), obtained using three-dimensional computer simulation.
In Fig. Figure 1 shows the homogeneous and vortex magnetization distributions calculated by modern numerical methods [5] in spherical cobalt nanoparticles of different diameters. Three-dimensional distributions of the magnetization vector in these particles are represented in these figures by arrows of fixed length. To determine the single-domain diameter of a spherical cobalt nanoparticle, it is necessary to count the energy diagram of these states, schematically shown in Fig. 2

Fig. 2. Schematic energy diagram of stable magnetic states of a nanoparticle depending on its radius.
As can be seen from Fig. 2, the total specific energy of a uniformly magnetized state of a particle (black line) does not depend on the radius of the particle, while the total energy of the vortex state (red curve) decreases rapidly with increasing its radius. The intersection point of these curves determines the single-domain radius of the particle ac = Dc / 2. If the particle radius is r <ac, then the homogeneous state has the lowest total energy, while the vortex state in a certain region of the radii can exist as metastable, that is, it can be stable, but it can have more energy. If r> ac, then the lowest energy vortex state will be. In this case, a homogeneous state can exist as a metastable in the range of radii ac <r <Rc, where Rc is the radius of stability of the homogeneous state.
For most technical applications, it is convenient to work with an ensemble of single-domain nanoparticles, whose properties can be relatively accurately predicted and controlled. A single-domain nanoparticle in all circumstances retains its full magnetic moment, while the average magnetic moment of a particle in the vortex state may be small, since the magnetic vectors in this state close themselves to themselves. For a particle in the vortex state, the average value of the magnetic moment substantially depends on the magnitude of the external magnetic field acting on the particle. From the diagram Fig. 2 shows that if the ensemble has a variation of nanoparticles in size near the single-domain radius, then in fact such an ensemble is an uncontrollable mixture of particles with different properties, single-domain and non-single-domain. If we also take into account that the value of the single-domain radius depends on the shape of the particle (sphere, elongated or oblate spheroid), then the experimental situation becomes quite confusing.
We see that an ensemble of magnetic nanoparticles is a rather complex physical system, the properties of which are determined by many different factors. In most cases (although not always) the ensemble consists of nanoparticles of the same chemical composition. Consequently, the ensemble particles can be characterized by a single set of material magnetic parameters, that is, the saturation magnetization Ms, the type of magnetic anisotropy and the value of the magnetic anisotropy constant K. The magnetic anisotropy determines the selected directions (the so-called light axes) in space with respect to the axes of symmetry of the crystal. In the absence of an external magnetic field, the particle magnetization vector spontaneously orients along the easy axes of the magnetic crystal. But the assignment of magnetic parameters alone is completely insufficient for the complete characterization of an ensemble of nanoparticles. It is necessary to know the distribution of nanoparticles in size and shape; the number and orientation of the light axes of nanoparticle anisotropy (oriented or non-oriented ensemble); distribution of nanoparticle centers in space. For example, the centers of nanoparticles can be located periodically, forming a certain spatial lattice, or occupy random positions, with some average distance between the particles.
Note that in real experiments, as a rule, fairly dense ensembles of particles are studied, whose properties differ significantly from the properties of rare ensembles. A theoretical study of the properties of a dense ensemble of particles is complicated by the long-range nature of the magnetic dipole interaction between the particles of the ensemble. Therefore, for an ensemble in which there are Np particles, it is necessary to take into account the Np2 pair interactions of the particles, so that the computational complexity quickly increases with the number of particles in the ensemble.
Further, the properties of the ensemble are significantly influenced by the environment in which the ensemble is located. It is necessary to distinguish mediums of relatively low viscosity, in which particles of an ensemble under the influence of an external magnetic field or magnetic dipole interaction of neighboring particles can be rotated as a whole, and media such as a solid matrix, in which rotation of nanoparticles as a whole is impossible. Finally, the ambient temperature can significantly affect the properties of an ensemble of particles of sufficiently small size (superparamagnetic nanoparticles). If the temperature of the medium exceeds the so-called blocking temperature of the magnetic moments of the nanoparticles, then the temperature fluctuations of the magnetic moments of individual particles significantly reduce the average magnetic moment of the ensemble.
Let us turn to the technical applications. The magnetic moment of a single-domain magnetic nanoparticle with uniaxial magnetic anisotropy has two distinct directions in space. At a sufficiently low (for example, room) temperature, in each of these two magnetic states the particle can be indefinitely long. Thus, it retains the memory of the acquired magnetic state, which means that it can store information without loss for quite a long time. If we conditionally assign the value “0” to the direction of the magnetic moment of the particle up, and the value “1” to the direction of the magnetic moment down, as shown in Fig. 3 on the left, then some binary text from a sequence of zeros and ones can be stored in a specially prepared magnetic state of the nanoparticle ensemble. Currently, in the process of magnetic recording, one bit of information is recorded not on one, but on a whole set of 20-40 closely spaced magnetic nanoparticles. The transition to the recording by the principle of “one bit - one particle” would significantly increase the density of magnetic information recording.
Clearly, however, significant technical difficulties that must be overcome to implement this interesting idea. First, the particles of the ensemble should be substantially the same and periodically located in a plane, with a lattice period, of the order of the size of the nanoparticle. It is all the more surprising that chemists have recently learned how to create similar, almost ideally periodic structures of magnetic nanoparticles using self-assembly processes, that is, self-organization of particles in an ensemble during their growth during a chemical reaction (see Fig. 3, right).

Fig. 3. The principle of super dense magnetic information recording on individual magnetic nanoparticles with two magnetic states (left) and the periodic structure of magnetic FePt nanoparticles obtained by the chemical method of self-assembly.
However, to implement the idea of super dense recording of information, besides the realization of the correct geometric structure of the ensemble, it is necessary to ensure a sufficiently large value of the magnetic anisotropy constant of the synthesized nanoparticles. In principle, FePt particles with the correct crystal structure, in which the planes of iron atoms alternate regularly with the planes of platinum atoms, have a record high magnetic anisotropy constant, K = 5 * 107 erg / cm3, [7] This allows maintaining the stability of the magnetic state of the particle time and for particles of sufficiently small diameter.
Indeed, to transfer the magnetic moment of a particle between two directions of easy magnetization, it is necessary to overcome the energy barrier of height
 where V is the volume of the nanoparticle. To prevent spontaneous moment transfer due to thermal fluctuations for a sufficiently long time (10 years), the hard condition KV> (50 - 70) kBT must be met, [7] where T is the ambient temperature, kB is the Boltzmann constant. With a decrease in the particle diameter, the energy barrier rapidly decreases, but the large value of the magnetic anisotropy constant of the particle makes it possible to maintain the indicated inequality for particles of nanometer size. Unfortunately, the FePt particles grown by self-assembly [6] are in a time-oriented magnetic state, when the iron and platinum atoms occupy arbitrary positions in the crystal lattice. And in this case, the constant of magnetic anisotropy of the substance is small, several orders of magnitude less than the specified passport value. Despite significant efforts to convert FePt particles to an ordered magnetic state using annealing and other methods, this fundamental problem has not yet been solved. In general, the problem of the influence of temperature fluctuations of their magnetic moments on the magnetic state of small particles is known as the superparamagnetic limit [7], and is still waiting to be resolved.
where V is the volume of the nanoparticle. To prevent spontaneous moment transfer due to thermal fluctuations for a sufficiently long time (10 years), the hard condition KV> (50 - 70) kBT must be met, [7] where T is the ambient temperature, kB is the Boltzmann constant. With a decrease in the particle diameter, the energy barrier rapidly decreases, but the large value of the magnetic anisotropy constant of the particle makes it possible to maintain the indicated inequality for particles of nanometer size. Unfortunately, the FePt particles grown by self-assembly [6] are in a time-oriented magnetic state, when the iron and platinum atoms occupy arbitrary positions in the crystal lattice. And in this case, the constant of magnetic anisotropy of the substance is small, several orders of magnitude less than the specified passport value. Despite significant efforts to convert FePt particles to an ordered magnetic state using annealing and other methods, this fundamental problem has not yet been solved. In general, the problem of the influence of temperature fluctuations of their magnetic moments on the magnetic state of small particles is known as the superparamagnetic limit [7], and is still waiting to be resolved.So, the temperature fluctuations of the magnetic moments of the particles lead to considerable difficulties in creating magnetic carriers for superdense recording of information. At the same time, they prove to be very useful for the development of one of the interesting biomedical applications of magnetic nanoparticles, namely, the method of magnetic hyperthermia, intended for the treatment of dangerous oncological diseases. It was experimentally proved [8] that maintaining the temperature of the affected organ is about 42 ° C for 20 to 30 minutes. leads to necrosis of cancer cells, more susceptible to elevated temperature than normal tissue. Many ferromagnetic materials are able to absorb the energy of an external alternating magnetic field and thereby heat the surrounding tissue. However, magnetic nanoparticles have significant advantages for magnetic hyperthermia, because: a) ensembles of superparamagnetic nanoparticles are capable of providing extremely large values of specific energy absorption, of the order of 1 kW per gram of substance; b) due to their small size, nanoparticles can penetrate deeply into biological materials; c) iron oxide nanoparticles are non-toxic, or slightly toxic, for a living organism, d) they have short periods of elimination from the body.
As we saw above, a magnetic nanoparticle is a very strong natural magnet, since the characteristic magnetic reversal field of even a magnetically soft particle of iron oxide at room temperature is quite large, Hc (0) ~ 2K / Ms ~ 400 E. It is important, however, that barrier separating magnetic potential wells,
 decreases with decreasing volume of the particle, V ~ R3, and can be compared with the characteristic thermal energy kBT. In this case, due to thermal fluctuations of the magnetic moment, the particle loses its average constant magnetization, becoming superparamagnetic. The characteristic residence time of the magnetic moment in a given potential well (Neel relaxation time) is estimated as
decreases with decreasing volume of the particle, V ~ R3, and can be compared with the characteristic thermal energy kBT. In this case, due to thermal fluctuations of the magnetic moment, the particle loses its average constant magnetization, becoming superparamagnetic. The characteristic residence time of the magnetic moment in a given potential well (Neel relaxation time) is estimated as 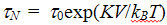 where is a constant
where is a constant  [9]. The relaxation time decreases exponentially rapidly with decreasing particle diameter. Once
[9]. The relaxation time decreases exponentially rapidly with decreasing particle diameter. Once 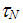 becomes of the order or less than the characteristic time of measurement of the magnetic moment
becomes of the order or less than the characteristic time of measurement of the magnetic moment  , the average magnetic moment of the particle is equal to zero.
, the average magnetic moment of the particle is equal to zero.But the phenomenon of superparamagnetism has a positive side. Thermal fluctuations, swinging the magnetic moment of the particles in the potential well, effectively lower the energy barrier and significantly reduce the magnitude of the particle magnetization reversal field. Therefore, an ensemble of superparamagnetic particles is able to magnetize in an external alternating magnetic field of moderate amplitude, H0 ~ 100 - 200 Oe, which is extremely important for magnetic hyperthermia, since it simplifies the conditions for creating an alternating magnetic field and reduces the cost of the necessary equipment.
As is known from thermodynamics [1,2], the intensity of the absorption of the energy of an alternating magnetic field is proportional to the area of the hysteresis loop of an ensemble of magnetic nanoparticles. In our group, theoretical calculations were carried out of low-frequency hysteresis loops of sparse ensembles of magnetic nanoparticles of various types [10, 11], as well as the corresponding experimental measurements performed by the original method [12, 13]. Theoretical calculations showed a significant dependence of the hysteresis loops on the frequency of the alternating magnetic field, as shown in Fig. four.

Fig. 4. Magnetic nanoparticles are able to effectively remotely absorb the energy of an alternating external magnetic field, and thereby heat the environment. However, this ability significantly depends on the frequency of exposure, and a number of other physical parameters.
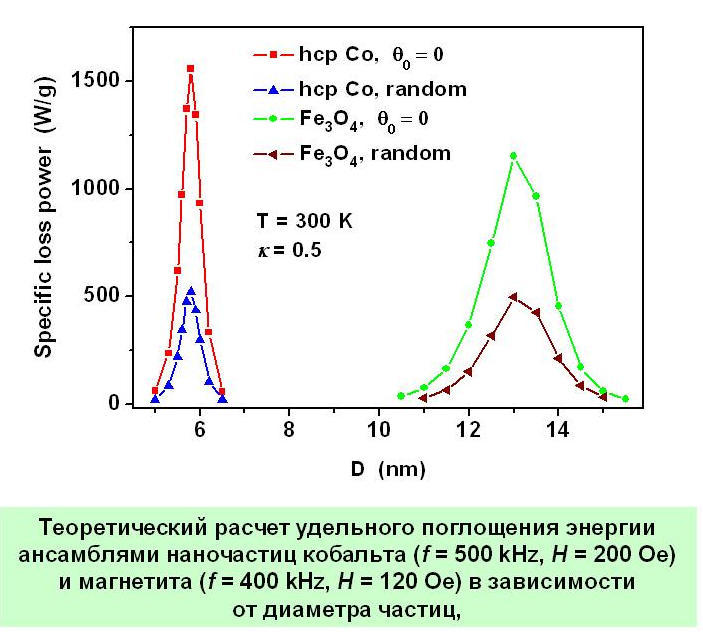
Theoretical analysis shows [10] (see Fig. 5) that the hysteresis loops of a superparamagnetic ensemble also very strongly depend on the average particle diameter, if the particles are fixed in the surrounding nonmagnetic medium. This important fact was confirmed in a number of recent experiments, although at the same time a significant dependence of specific energy absorption on a number of other factors was demonstrated, such as the influence of the magnetic dipole interaction in dense assemblies of magnetic nanoparticles [12, 13].

Fig. 5. Theoretical calculation [] of the specific energy absorption of an alternating magnetic field by sparse ensembles of cobalt nanoparticles (f = 500 kHz, H = 200 Oe) and magnetite (f = 400 kHz, H = 120 Oe) depending on the particle diameter.
Magnetic hyperthermia, being a local and distant effect, apparently, does not have such serious side effects as chemotherapy or radiotherapy [8]. It seems that the successful development of magnetic hyperthermia will depend on the successful solution of several problems. First of all, it is necessary to improve the methods of preparation of nanoparticle ensembles with a sufficiently large specific energy absorption in a variable magnetic field of moderate amplitude. This will reduce the dose of nanoparticles, sufficient to achieve a positive therapeutic effect. Ideally, it would be desirable to learn how to locally heat small volumes of tissue in order to suppress small, very dangerous neoplasms at an early stage. Further, it is necessary to ensure the creation of an alternating magnetic field of sufficient amplitude, with the necessary spatial distribution in a given area of the body, at reasonable energy costs, guaranteed safety from electric shock, of moderate cost. Finally, it is necessary to learn how to control the exposure itself, selecting the amplitude and frequency of the magnetic field, the magnetic and geometric parameters of the nanoparticles, the time and frequency of exposure, taking into account the electrodynamic and thermal parameters of the medium. It is also highly desirable to control the spatial and temporal distribution of temperature in the area of impact. Currently, these problems are in the center of attention of researchers in various fields.
Quoted literature
[1] G. S. Krinchik, Physics of Magnetic Phenomena (Moscow, Moscow State University, 1985).
[2] S.V. Vonsovsky, Magnetism (Moscow, Science, 1972).
[3] L. Landau and E. Lifshitz, Phys. Z. Sowjetunion 8, 153 (1935).
[4] WF Brown, Jr., Micromagnetics (Wiley-Interscience, New York - London, 1963)
[5] NA Usov and JW Tucker. Material Science Forum 373-376, 429 (2001).
[6] S. Sun, CB Murray, D. Weller, L. Folks, and A. Moser, Science 287, 1989 (2000).
[7] D. Weller and A. Moser, IEEE Trans. Magn. 35, 4423 (1999).
[8] QA Pankhurst, NKT Thanh, SK Jones, J. Dobson, J. Phys. D: Appl. Phys. 42, 224001 (2009).
[9] WF Brown, Jr., Phys. Rev. 130, 1677 (1963).
[10] NA Usov, J. Appl. Phys. 107, 123909 (2010).
[11] NA Usov, B.Ya. Liubimov, J. Appl. Phys. 112, 023901 (2012).
[12] SA Gudoshnikov, B. Ya. Liubimov, and NA Usov, AIP Advances 2, 012143 (2012)
[13] SA Gudoshnikov, B.Ya. Liubimov, AV Popova, NA Usov. J. Magn. Magn. Mater. 324, 3690 (2012)
[2] S.V. Vonsovsky, Magnetism (Moscow, Science, 1972).
[3] L. Landau and E. Lifshitz, Phys. Z. Sowjetunion 8, 153 (1935).
[4] WF Brown, Jr., Micromagnetics (Wiley-Interscience, New York - London, 1963)
[5] NA Usov and JW Tucker. Material Science Forum 373-376, 429 (2001).
[6] S. Sun, CB Murray, D. Weller, L. Folks, and A. Moser, Science 287, 1989 (2000).
[7] D. Weller and A. Moser, IEEE Trans. Magn. 35, 4423 (1999).
[8] QA Pankhurst, NKT Thanh, SK Jones, J. Dobson, J. Phys. D: Appl. Phys. 42, 224001 (2009).
[9] WF Brown, Jr., Phys. Rev. 130, 1677 (1963).
[10] NA Usov, J. Appl. Phys. 107, 123909 (2010).
[11] NA Usov, B.Ya. Liubimov, J. Appl. Phys. 112, 023901 (2012).
[12] SA Gudoshnikov, B. Ya. Liubimov, and NA Usov, AIP Advances 2, 012143 (2012)
[13] SA Gudoshnikov, B.Ya. Liubimov, AV Popova, NA Usov. J. Magn. Magn. Mater. 324, 3690 (2012)
Source: https://habr.com/ru/post/390127/
All Articles