Entertainment on the Lobachevsky plane

Euclidean plane is boring. Available space grows only as a square of the radius of view. Compared with her open spaces Lobachevsky's giant. But there is life there too !
The sum of the angles of the polygon here is smaller than that of Euclid and is not constant, but depends on the area (from here an interesting consequence - there are the largest triangles, four-five-and-n squares, the sum of the angles which becomes zero). Therefore, there are plane tilings by any regular polygons, if they are large enough. In the article about the game Life, paving with quadrilaterals is used, at each vertex five quadrangles converge. But such quadrangles are very large. If we reject the similarity of polygons, we can take a tiling from regular hexagons and heptagons. For it, you can make a visual model of the plane of the magnetic balls "Neokub".

Polygons will be rings of six and seven balls. Rings can be interconnected. If they are of the same orientation (the direction of the magnetic field in the ring), they are linked by ribs of two balls, if different - by an edge with a vertex. Each heptagon is in contact with seven hexagons.

Each hexagon has three heptagons and three hexagons.

A small piece of the plane begins to gather in the folds, with further growth to lay in our space is no longer possible. But you can cut a strip of equal width (limited not by straight lines, but by hypercycles ), then it can be rolled up into a spiral.
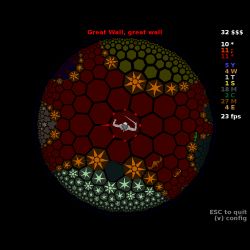
The computer is not so strongly limited by the geometry of the real space and you can walk on the Lobachevsky plane in a hyperrogue . After playing this game you can feel some features of hyperbolic geometry. The local version of the Pythagorean theorem is written as follows: ch (c) = ch (a) ch (b) (by ch we denote the hyperbolic cosine ). For small lengths, it turns into the usual Pythagorean theorem (this can be easily verified by expanding ch in a Taylor series to a second degree). For large (ch becomes almost equal to half of the exponent) - the hypotenuse approaches the simple sum of the legs. That is, it does not make much sense to run across the path and it becomes easier to run away than to catch up. The circumference length tends to an exponential radius — it takes a very long time to avoid obstacles.
Unfortunately, I did not find strategic games on the Lobachevsky plane. Since the perimeter and area of ​​the figures grows about the same, control of a large area will not give a serious advantage in the defense of the borders. And since the area of ​​the circle is growing exponentially, it would be possible to compactly place huge armies. In my opinion, this would make the game more interesting.
It is a pity that the geometry of our world on a foreseeable scale is not hyperbolic ...