Entropy? It's simple!
This post is a free translation of the answer that Mark Eichenlaub gave to the question “ What is an intuitive way to understand entropy?” specified on the Quora website
Entropy. Perhaps this is one of the most difficult to understand concepts with which you can meet in the course of physics, at least if we talk about classical physics. Few graduate students in physics can explain what it is. Most problems with understanding entropy, however, can be removed if one thing is understood. Entropy is qualitatively different from other thermodynamic quantities: such as pressure, volume, or internal energy, because it is not a property of the system, but of how we consider this system. Unfortunately in the course of thermodynamics, it is usually considered on a par with other thermodynamic functions, which exacerbates misunderstanding.
In a nutshell, then
For example, if you ask me where I live, and I will answer: in Russia, then my entropy will be high for you, after all, Russia is a big country. If I give you my zip code: 603081, then my entropy will decrease for you, since you will get more information.
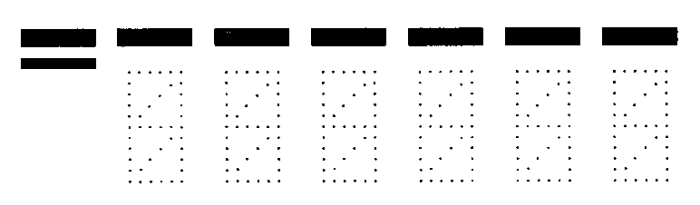
The zip code is six digits, so I gave you six characters of information. The entropy of your knowledge about me has dropped by about 6 characters. (Actually, not really, because some indices respond to more addresses, and some to smaller ones, but we neglect this).

Or consider another example. Suppose I have ten dice (hexagonal bones), and throwing them out, I inform you that their sum is equal to 30. Knowing only this, you cannot tell which specific numbers on each of the bones - you lack information. These specific numbers on bones in statistical physics are called microstates, and the total amount (30 in our case) is called the macrostate. There are 2,930,455 microstates, which correspond to the sum equal to 30. So the entropy of this macrostate is approximately 6.5 characters (the half comes from the fact that when the microstates are numbered in order in the seventh digit, not all digits are available, but only 0, 1 and 2).
And what if I told you that the amount is 59? For this macrostate, there are only 10 possible microstates, so its entropy is only one character. As you can see, different macrostates have different entropies.
')
Let me now tell you that the sum of the first five bones is 13, and the sum of the remaining five is 17, so the total amount is again 30. You, however, have more information in this case, therefore the system entropy for you should fall. And, indeed, 13 on five bones can be obtained in 420 different ways, and 17 - 780, that is, the total number of microstates will be only 420x780 = 327 600. The entropy of such a system is approximately one character less than in the first example.
We measure entropy as the number of characters needed to record the number of microstates. Mathematically, this number is defined as the logarithm, therefore denoting the entropy as S, and the number of microstates as Ω, we can write:
S = log Ω
This is nothing more than the Boltzmann formula (up to a factor k, which depends on the chosen units) for entropy. If the macrostate corresponds to one microstate, its entropy by this formula is zero. If you have two systems, then the total entropy is equal to the sum of the entropies of each of these systems, because log (AB) = log A + log B.

From the above description, it becomes clear why one should not think of entropy as a property of the system. The system has a certain internal energy, impulse, charge, but it does not have a certain entropy: the entropy of ten bones depends on whether you know only their full sum, or also the partial sums of the five of the bones.
In other words, entropy is how we describe the system. And this makes it very different from other quantities with which it is customary to work in physics.
The classical system that is considered in physics is gas in a vessel under the piston. The microstate of a gas is the position and momentum (speed) of each of its molecules. This is equivalent to knowing the value that fell on each bone in the earlier example. The gas macrostate is described by values such as pressure, density, volume, chemical composition. It is like the sum of the values dropped on the bones.

The quantities describing the macrostate can be related to each other through the so-called "equation of state". It is the presence of this connection that allows us, without knowing the microstates, to predict what will happen to our system if we start to heat it up or move the piston. For an ideal gas, the equation of state has a simple form:
p = ρT
although you are most likely familiar with the Clapeyron – Mendeleev equation pV = νRT — this is the same equation, only with the addition of a pair of constants to confuse you. The more microstates correspond to this macrostate, that is, the more particles are part of our system, the better the equation of state it describes. For gas, the characteristic values of the number of particles are equal to the Avogadro number, that is, they are of the order of 10 23 .
Values such as pressure, temperature, and density are called averaged, because they are the average manifestation of constantly changing microstates corresponding to a given macrostate (or, rather, closest to it macrostate). To find out in which microstate the system is, we need a lot of information - we need to know the position and speed of each particle. The amount of this information is called entropy.
How does entropy change with the macrostate change? It is easy to understand. For example, if we heat the gas a little, the speed of its particles will increase, therefore, the degree of our ignorance about this speed will also increase, that is, the entropy will increase. Or, if we increase the gas volume by retracing the piston, the degree of our ignorance of the position of the particles will increase, and the entropy will also increase.
If instead of gas we consider some solid body, especially with an ordered structure, as in crystals, for example, a piece of metal, then its entropy will be small. Why? Because knowing the position of one atom in such a structure, you know the position of all the others (they are also built in the correct crystal structure), the speeds of atoms are small, because they cannot fly away from their position and only slightly fluctuate around the equilibrium position.
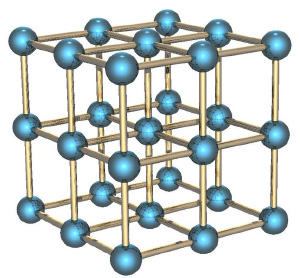
If a piece of metal is in the field of the aggression (for example, raised above the surface of the Earth), then the potential energy of each atom in the metal is approximately equal to the potential energy of other atoms, and the entropy associated with this energy is low. This distinguishes potential energy from kinetic energy, which for thermal motion can vary greatly from atom to atom.
If a piece of metal, raised to a certain height, is released, then its potential energy will transfer to kinetic energy, but the entropy will practically not increase, because all atoms will move approximately equally. But when a piece falls to the ground, during an impact, the atoms of the metal will get a random direction of movement, and the entropy will increase dramatically. The kinetic energy of directional motion will transfer to the kinetic energy of thermal motion. Before the impact, we knew approximately how each atom moves, now we have lost this information.
The second law of thermodynamics states that entropy (of a closed system) never decreases. We can now understand why: because suddenly it is impossible to get more information about microstates. Once you have lost some information about the microstate (like when you hit a piece of metal on the ground), you cannot bring it back.

Let's go back to the dice. Recall that the macrostate with the sum of 59 has a very low entropy, but it is not so easy to get it. If you throw the bones over and over again, then the sums (macrostates) that meet the greater number of microstates will fall out, that is, the macrostates with large entropy will be realized. The largest entropy has a sum of 35, and it is she who will fall out more often than others. This is what the second law of thermodynamics says. Any random (uncontrolled) interaction leads to an increase in entropy, at least until it reaches its maximum.
And one more example to consolidate what was said. Suppose we have a container in which there are two gases, separated by a partition located in the middle of the container. Let's call the molecules of one gas blue, and the other red.
If you open the partition, the gases will begin to mix, because the number of microstates in which the gases are mixed is much more than the microstates in which they are separated, and all the microstates are naturally equiprobable. When we opened the partition, for each molecule we lost information on which side of the partition it now lies. If the molecules were N, then N bits of information are lost (bits and symbols, in this context, this is, in fact, the same thing, and differ only in a certain constant multiplier).
And finally, we will consider a solution within our paradigm of the famous Maxwell demon paradox. Let me remind you that it is as follows. Suppose we have mixed gases of blue and red molecules. We put back the partition, having made a small hole in it, into which we will put an imaginary demon. His task is to skip from left to right only the reds, and from right to left only the blues. It is obvious that after some time the gases will be separated again: all blue molecules will be on the left of the partition, and all of the red will be on the right.
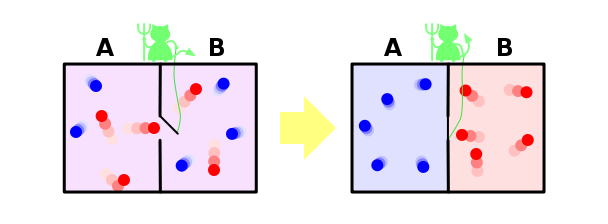
It turns out that our demon lowered the entropy of the system. Nothing happened to the demon, that is, its entropy has not changed, and our system was closed. It turns out that we have found an example when the second law of thermodynamics is not satisfied! How was it possible?
This paradox is solved, however, very simply. After all, entropy is a property not of a system, but of our knowledge about this system. We all know little about the system, so it seems to us that its entropy decreases. But our demon knows a lot about the system - to separate molecules, he must know the position and speed of each of them (at least on the way up to him). If he knows everything about molecules, then from his point of view, the entropy of the system, in fact, is zero - he simply does not have the missing information about it. In this case, the entropy of the system was zero, remained zero, and the second law of thermodynamics was not violated anywhere.
But even if the demon does not know all the information about the microstate of the system, he, at a minimum, needs to know the color of the molecule flying up to him in order to understand whether to skip it or not. And if the total number of molecules is N, then the daemon should have N bits of information about the system — but that is how much information we lost when the partition was opened. That is, the amount of information lost is exactly equal to the amount of information that needs to be obtained about the system in order to return it to its original state - and this sounds quite logical, and again does not contradict the second law of thermodynamics.
Entropy. Perhaps this is one of the most difficult to understand concepts with which you can meet in the course of physics, at least if we talk about classical physics. Few graduate students in physics can explain what it is. Most problems with understanding entropy, however, can be removed if one thing is understood. Entropy is qualitatively different from other thermodynamic quantities: such as pressure, volume, or internal energy, because it is not a property of the system, but of how we consider this system. Unfortunately in the course of thermodynamics, it is usually considered on a par with other thermodynamic functions, which exacerbates misunderstanding.
So what is entropy?
In a nutshell, then
Entropy is how much information you don't know about the system.
For example, if you ask me where I live, and I will answer: in Russia, then my entropy will be high for you, after all, Russia is a big country. If I give you my zip code: 603081, then my entropy will decrease for you, since you will get more information.

The zip code is six digits, so I gave you six characters of information. The entropy of your knowledge about me has dropped by about 6 characters. (Actually, not really, because some indices respond to more addresses, and some to smaller ones, but we neglect this).

Or consider another example. Suppose I have ten dice (hexagonal bones), and throwing them out, I inform you that their sum is equal to 30. Knowing only this, you cannot tell which specific numbers on each of the bones - you lack information. These specific numbers on bones in statistical physics are called microstates, and the total amount (30 in our case) is called the macrostate. There are 2,930,455 microstates, which correspond to the sum equal to 30. So the entropy of this macrostate is approximately 6.5 characters (the half comes from the fact that when the microstates are numbered in order in the seventh digit, not all digits are available, but only 0, 1 and 2).
And what if I told you that the amount is 59? For this macrostate, there are only 10 possible microstates, so its entropy is only one character. As you can see, different macrostates have different entropies.
')
Let me now tell you that the sum of the first five bones is 13, and the sum of the remaining five is 17, so the total amount is again 30. You, however, have more information in this case, therefore the system entropy for you should fall. And, indeed, 13 on five bones can be obtained in 420 different ways, and 17 - 780, that is, the total number of microstates will be only 420x780 = 327 600. The entropy of such a system is approximately one character less than in the first example.
We measure entropy as the number of characters needed to record the number of microstates. Mathematically, this number is defined as the logarithm, therefore denoting the entropy as S, and the number of microstates as Ω, we can write:
S = log Ω
This is nothing more than the Boltzmann formula (up to a factor k, which depends on the chosen units) for entropy. If the macrostate corresponds to one microstate, its entropy by this formula is zero. If you have two systems, then the total entropy is equal to the sum of the entropies of each of these systems, because log (AB) = log A + log B.

From the above description, it becomes clear why one should not think of entropy as a property of the system. The system has a certain internal energy, impulse, charge, but it does not have a certain entropy: the entropy of ten bones depends on whether you know only their full sum, or also the partial sums of the five of the bones.
In other words, entropy is how we describe the system. And this makes it very different from other quantities with which it is customary to work in physics.
Physical example: gas under the piston
The classical system that is considered in physics is gas in a vessel under the piston. The microstate of a gas is the position and momentum (speed) of each of its molecules. This is equivalent to knowing the value that fell on each bone in the earlier example. The gas macrostate is described by values such as pressure, density, volume, chemical composition. It is like the sum of the values dropped on the bones.

The quantities describing the macrostate can be related to each other through the so-called "equation of state". It is the presence of this connection that allows us, without knowing the microstates, to predict what will happen to our system if we start to heat it up or move the piston. For an ideal gas, the equation of state has a simple form:
p = ρT
although you are most likely familiar with the Clapeyron – Mendeleev equation pV = νRT — this is the same equation, only with the addition of a pair of constants to confuse you. The more microstates correspond to this macrostate, that is, the more particles are part of our system, the better the equation of state it describes. For gas, the characteristic values of the number of particles are equal to the Avogadro number, that is, they are of the order of 10 23 .
Values such as pressure, temperature, and density are called averaged, because they are the average manifestation of constantly changing microstates corresponding to a given macrostate (or, rather, closest to it macrostate). To find out in which microstate the system is, we need a lot of information - we need to know the position and speed of each particle. The amount of this information is called entropy.
How does entropy change with the macrostate change? It is easy to understand. For example, if we heat the gas a little, the speed of its particles will increase, therefore, the degree of our ignorance about this speed will also increase, that is, the entropy will increase. Or, if we increase the gas volume by retracing the piston, the degree of our ignorance of the position of the particles will increase, and the entropy will also increase.
Solids and potential energy
If instead of gas we consider some solid body, especially with an ordered structure, as in crystals, for example, a piece of metal, then its entropy will be small. Why? Because knowing the position of one atom in such a structure, you know the position of all the others (they are also built in the correct crystal structure), the speeds of atoms are small, because they cannot fly away from their position and only slightly fluctuate around the equilibrium position.

If a piece of metal is in the field of the aggression (for example, raised above the surface of the Earth), then the potential energy of each atom in the metal is approximately equal to the potential energy of other atoms, and the entropy associated with this energy is low. This distinguishes potential energy from kinetic energy, which for thermal motion can vary greatly from atom to atom.
If a piece of metal, raised to a certain height, is released, then its potential energy will transfer to kinetic energy, but the entropy will practically not increase, because all atoms will move approximately equally. But when a piece falls to the ground, during an impact, the atoms of the metal will get a random direction of movement, and the entropy will increase dramatically. The kinetic energy of directional motion will transfer to the kinetic energy of thermal motion. Before the impact, we knew approximately how each atom moves, now we have lost this information.
We understand the second law of thermodynamics
The second law of thermodynamics states that entropy (of a closed system) never decreases. We can now understand why: because suddenly it is impossible to get more information about microstates. Once you have lost some information about the microstate (like when you hit a piece of metal on the ground), you cannot bring it back.

Let's go back to the dice. Recall that the macrostate with the sum of 59 has a very low entropy, but it is not so easy to get it. If you throw the bones over and over again, then the sums (macrostates) that meet the greater number of microstates will fall out, that is, the macrostates with large entropy will be realized. The largest entropy has a sum of 35, and it is she who will fall out more often than others. This is what the second law of thermodynamics says. Any random (uncontrolled) interaction leads to an increase in entropy, at least until it reaches its maximum.
Gas mixing
And one more example to consolidate what was said. Suppose we have a container in which there are two gases, separated by a partition located in the middle of the container. Let's call the molecules of one gas blue, and the other red.
If you open the partition, the gases will begin to mix, because the number of microstates in which the gases are mixed is much more than the microstates in which they are separated, and all the microstates are naturally equiprobable. When we opened the partition, for each molecule we lost information on which side of the partition it now lies. If the molecules were N, then N bits of information are lost (bits and symbols, in this context, this is, in fact, the same thing, and differ only in a certain constant multiplier).
We deal with Maxwell's demon
And finally, we will consider a solution within our paradigm of the famous Maxwell demon paradox. Let me remind you that it is as follows. Suppose we have mixed gases of blue and red molecules. We put back the partition, having made a small hole in it, into which we will put an imaginary demon. His task is to skip from left to right only the reds, and from right to left only the blues. It is obvious that after some time the gases will be separated again: all blue molecules will be on the left of the partition, and all of the red will be on the right.

It turns out that our demon lowered the entropy of the system. Nothing happened to the demon, that is, its entropy has not changed, and our system was closed. It turns out that we have found an example when the second law of thermodynamics is not satisfied! How was it possible?
This paradox is solved, however, very simply. After all, entropy is a property not of a system, but of our knowledge about this system. We all know little about the system, so it seems to us that its entropy decreases. But our demon knows a lot about the system - to separate molecules, he must know the position and speed of each of them (at least on the way up to him). If he knows everything about molecules, then from his point of view, the entropy of the system, in fact, is zero - he simply does not have the missing information about it. In this case, the entropy of the system was zero, remained zero, and the second law of thermodynamics was not violated anywhere.
But even if the demon does not know all the information about the microstate of the system, he, at a minimum, needs to know the color of the molecule flying up to him in order to understand whether to skip it or not. And if the total number of molecules is N, then the daemon should have N bits of information about the system — but that is how much information we lost when the partition was opened. That is, the amount of information lost is exactly equal to the amount of information that needs to be obtained about the system in order to return it to its original state - and this sounds quite logical, and again does not contradict the second law of thermodynamics.
Source: https://habr.com/ru/post/374681/
All Articles