Ask Ethan: Where is the line between mathematics and physics?

Simulations of how a black hole in the center of the Milky Way might look to an Event Horizon Telescope telescope . In simulations it is assumed that the event horizon exists, that the relativistic equations are correct, and that we use the correct parameters of the system of interest to us.



When it comes to describing the physical world, we can do it sporadically, as is often the case, or use science. The latter option involves the collection of numerical data, the search for correlations between observations, the formulation of physical laws and theories, and the writing of equations that make it possible to predict the results of the development of various situations. The more advanced physical phenomena we describe, the more abstract and complex equations and theoretical platforms become. But while formulating these theories and writing equations describing what will happen under different conditions, are we moving from the world of physics to the world of mathematics? Where is the border between them? This is the question our reader asks:

Where to draw a line between abstract mathematics and physics? Does the Noether theorem relate to scientific knowledge or to mathematics? What about the Maldacena theory of AdS / CFT compliance ?

Fortunately, in order to find a difference, we don’t have to refer to such complex examples.







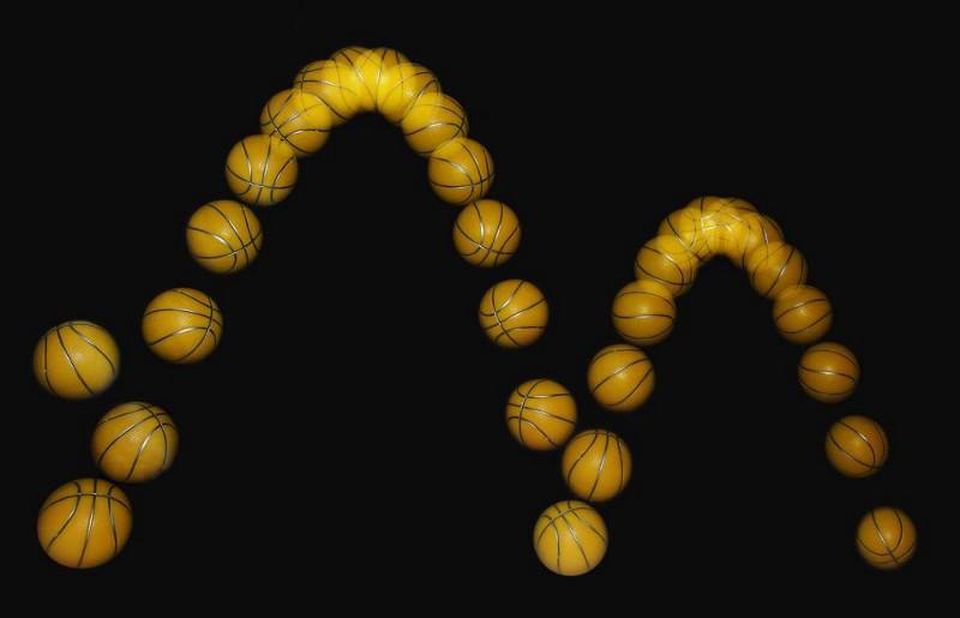
Knowing the position and velocity of a particle at any point of the trajectory, you can calculate where and when it hits the ground. But mathematically you get two solutions, and in order to choose the right one, you need to apply physics.

')

Suppose you perform such a simple action as throwing a ball. At any time, if you tell me where it is and how it moves (position and speed), I can predict where and when it hits the ground. But if you simply write and solve equations governed by the laws of motion of Newton, you will not get one correct answer. Instead, there will be two answers: one corresponding to the impact of the ball with the ground in the future, and the other showing where the ball would hit the ground in the past. Mathematics of equations does not tell you which of the answers, positive or negative, is physically correct. It's like asking what the square root of four is equal to: your instinct says “two,” but it could be minus two. Mathematics is not always deterministic in itself.







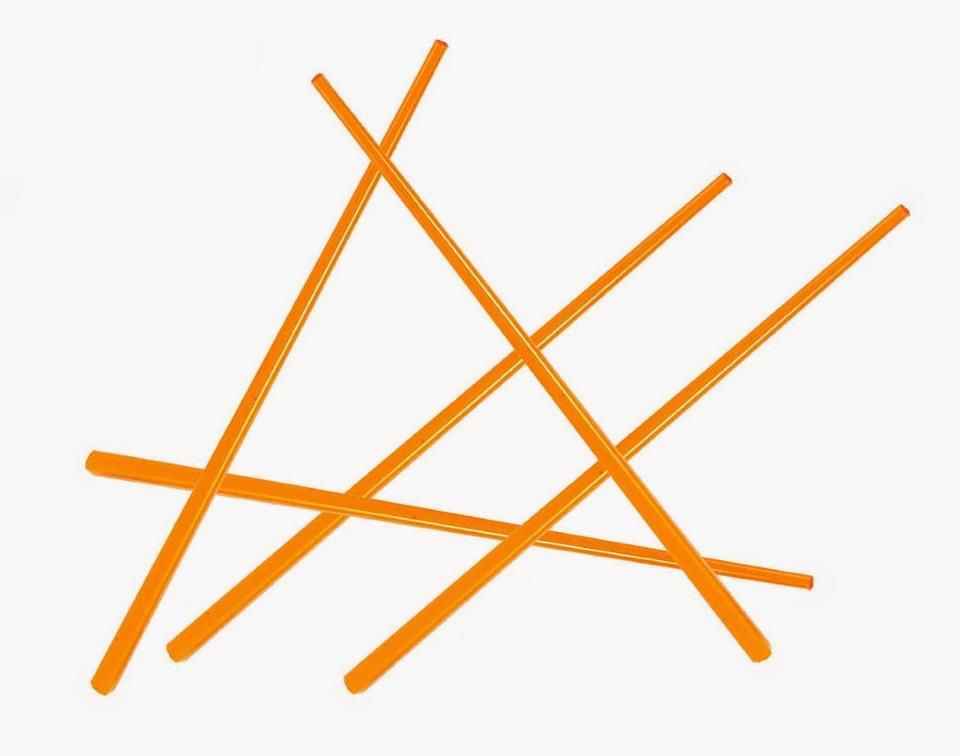
Five fallen chopsticks can form a triangle. But, as in many mathematical problems, there is a chance to get more than one triangle. Where there are many mathematical solutions, physics helps us to answer.



In fact, there is no universal rule that could be applied to find out what answer you need! This is the greatest difference between mathematics and physics: mathematics tells you all possible solutions, but physics allows you to choose a solution that describes our Universe.



An example, of course, is very simplified, and a fairly simple rule applies: choose a solution that lies in future time and space as you go. But this rule cannot be applied in any theory, for example, in the theory of relativity and quantum mechanics. When the equations are not so intuitive physically, it is much more difficult to know which of the possible solutions will be physically meaningful.







The mathematics that governs the General Theory of Relativity is quite complex, and GR itself offers many possible solutions to equations. But, only by defining conditions describing our Universe and comparing theoretical predictions with measurements and observations, we can get a physical theory.



What to do when mathematics becomes more abstract? What to do when you meet with GTR, quantum field theory, or even more abstract and speculative theory, like cosmic inflation, extra dimensions, theories of great unification, string theory? The mathematical structures that you create to describe these possibilities are nothing more than structures; by themselves, they will not give you physical ideas. But if you can extract either observables, or a relationship with physically observables, then you will begin to move into the area that you can check and observe.







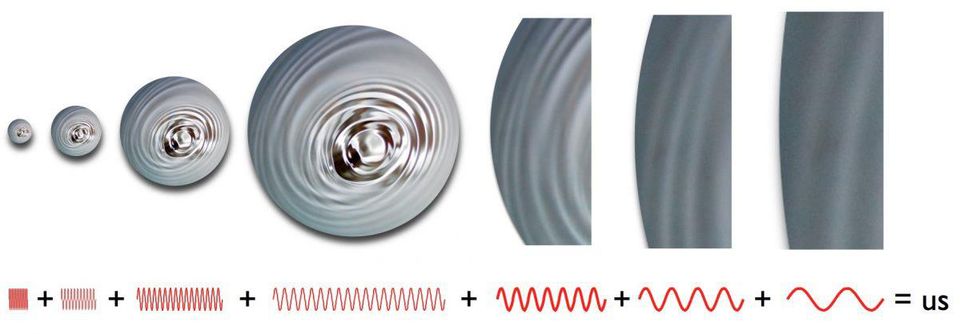
Quantum fluctuations that occur during inflation stretch across the entire Universe, but they also cause fluctuations in the total energy density, which leaves us with a nonzero spatial curvature of the Universe. These field fluctuations cause density imperfections in the early Universe, which leads to temperature fluctuations that we observe in the CMB.



For example, in inflationary cosmology there are many complex equations that control everything that happens. This is very similar to mathematics, and in many discussions it is not very similar to physics. But the main thing here is to combine the predictions of these mathematical equations with physical observations. For example, based on the existence of quantum fluctuations in the fabric of space, and stretching and expanding space at an exponential rate during inflation, we can expect ripples and imperfections in the value of the quantum field caused by inflation throughout the Universe. At the end of inflation, these fluctuations turn into density fluctuations, which we can see as temperature fluctuations in the residual luminescence of the Big Bang. This prediction of the 1980s was confirmed by satellites like COBE, WMAP and Planck many years later.







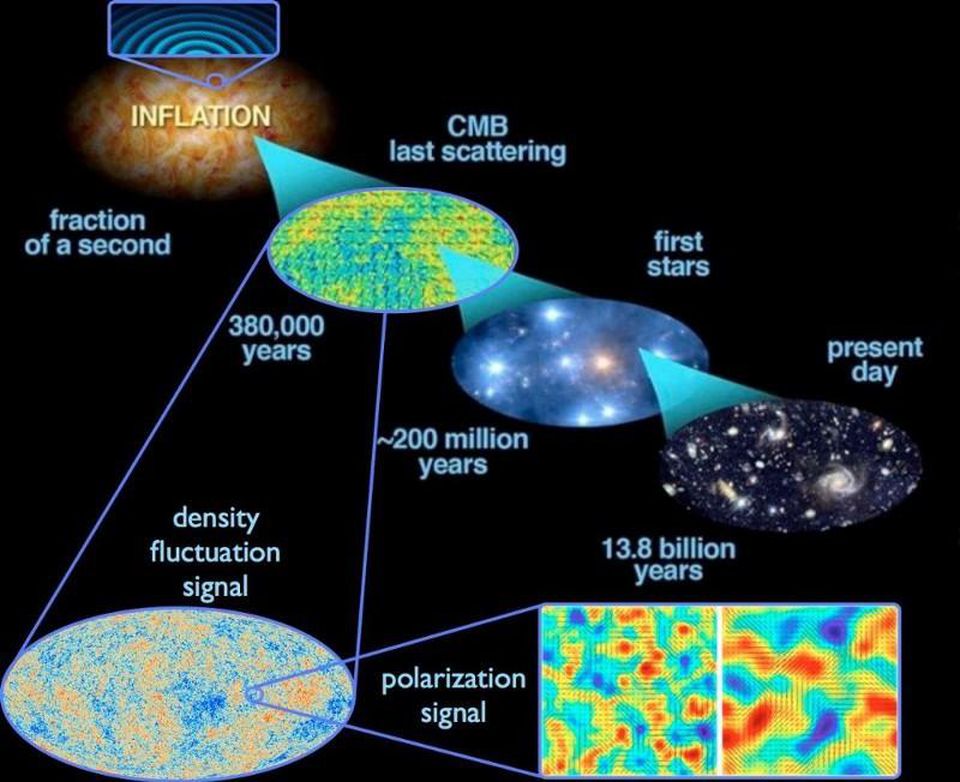
Quantum fluctuations that occur during inflation stretch across the universe, and when inflation ends, they become density fluctuations. Over time, this leads to the emergence of large-scale structures in today's Universe, as well as temperature fluctuations observed in relic radiation.



Noether's theorem is an interesting example of a mathematical theorem that has very serious mathematical consequences and also applies in a very special way to physics. In general, the theorem says that if you have a system that integrates the Lagrangian, and the system has symmetry, then some conserved value should be associated with this symmetry. In physics, the integral function of the Lagrangian corresponds to the "action", and therefore for any system that can be modeled using the Lagrangian, and containing symmetry, we can derive a certain conservation law. In physics, this allows us to derive such things as energy conservation, momentum conservation, and electrical charge conservation.







Different frames of reference, including different positions and motion, would be confronted with different laws of physics in the case of non-conservation of momentum. The fact that we have a symmetry of speed conversion tells us about the presence of a conserved quantity: a linear pulse.



What is interesting, if we could not describe the Universe with the help of mathematical equations containing these symmetries, there would be no reason to expect the conservation of these quantities. Therefore, many people are surprised that in GR there is no universal symmetry on the transfer in time, that is, for the expanding Universe in which we live, there is no law of conservation of energy! Separate interactions in quantum field theory obey this symmetry, so energy is conserved there. But energy is not even defined on the scale of the entire Universe, that is, we do not know whether it is conserved or not.







A two-dimensional projection of the Calabi-Yau variety , one popular compactification method for additional unnecessary measurements of string theory. Maldasena’s hypothesis is that the anti-Desitter space is mathematically dual to conformal field theories in a number of dimensions less than one.



The Maldasena hypothesis is even more complex. It is also known as AdS / CFT correspondence, and shows that there is mathematical duality — that is, the subordination of both systems to the same equations — between conformal field theory (something like strength in quantum mechanics) and string theory in anti-dessitter space with one extra dimension. If both systems are controlled by the same equations, they must have the same physics. So, in principle, we should be able to describe aspects of our four-dimensional (three spatial and one-time dimension) Universe in the same way as the five-dimensional anti-Desitter space-time with the correct parameters is described. This is one of the closest examples of applying the holographic principle to the Universe.



String theory (or, more precisely, string theory) has its own limitations, as does the interaction of the Universe, so it is not clear whether there is a one-to-one correspondence between our four-dimensional Universe, gravity, electromagnetism and nuclear forces, and some version of string theory. The hypothesis is interesting, and it has found certain applications in the real world: in the study of quark-gluon plasma. In this sense, it is already more than mathematics: it is physics. But where exactly it deviates from physics into the world of pure mathematics is not yet completely clear.







The Lagrangian of the Standard Model is a single equation that includes particles and the interactions of the Standard Model. It has five independent parts: gluons (1), weak bosons (2), interaction of matter with weak interaction and the Higgs field (3), spirits-particles, eliminating the redundancy of the Higgs field (4) and Faddeev-Popov spirits , affecting redundancy weak interaction (5). Neutrino masses are not included here. Describes everything we know today; it may not be a complete Lagrangian describing 3 or 4 fundamental interactions.



It all comes down to a more general question: how and when can we use mathematics to learn something about our physical universe? We do not know how, but we know when: when it is consistent with our experiments and observations. As long as all the laws of physics remain laws of physics, and are not turned on or off by caprice, and do not change in some strange way, we know that we can describe them mathematically, at least in principle. Therefore, mathematics is a set of tools that we use to describe the work of the universe. These are unprocessed materials: nails, boards, hammers and saws. Physics is how to apply this math. Physics is how to put it all together so that all your materials acquire meaning and become, for example, a house, instead of a set of materials that, in principle, can be used to build something completely different.







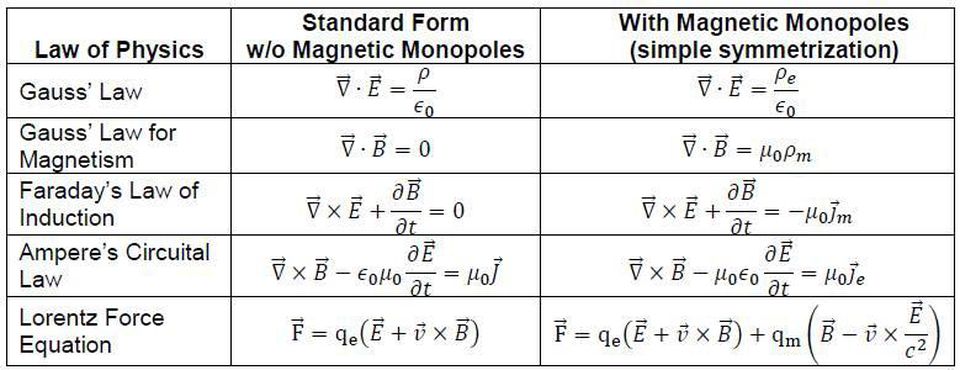
It is quite possible to write down various equations, such as Maxwell’s equations describing the Universe. We can write them in different ways, but only by comparing their predictions with physical observations, we can draw some conclusions about their truth. Therefore, the variant of Maxwell's equations with magnetic monopoles does not correspond to reality, and the variants without them correspond to.



If something describes the Universe accurately, and is capable of making numerical predictions, then this is physics. If these predictions prove to be accurate and reflect reality, then this is correct and useful physics. If one can demonstrate the falsity of these predictions, then this is physics that does not describe our Universe: this is a failed physical theory. But if the equations have no connection with the physical Universe, and they cannot be connected with anything that one could hope to ever see or measure, this is definitely a world of mathematics; then its separation from physics will be final. Mathematics is a language used to describe physics, but not everything mathematical has a physical meaning. The relationship between them and its violation can be determined only by observing the Universe itself.