Classic confusion associated with the Big Bang
One of the most confusing properties of the Big Bang is associated with the expansion of the universe. Any sensible person, having heard about the Big Bang, imagines something expanding that he has already seen in life: a cloud of smoke exploding outside, or an exploding balloon filled with air. It `s naturally. And presenting this, a reasonable person will ask the question: “But what is the Universe expanding into?”
This sensible, but, at first glance, paradoxical question is simply incorrectly asked. These are the consequences of what you imagined are completely different. I will try to correct the course of your thoughts.
Let's go back and look at fig. 3 of the article about one-dimensional worlds . I reproduced the part of this figure we need in fig. 1 in this article. Pay attention to two completely different representations of the aeolian line (measurements of possible wind directions, which include such directions as north, southeast, west-north-west, etc.). One of the representations is a line segment, the left end of which coincides with the right. The other is a loop on the plane. Just a second, you say - they look different. The loop surrounds a specific area, it has an inner and outer part. There is no such segment. So how can they portray the same thing?
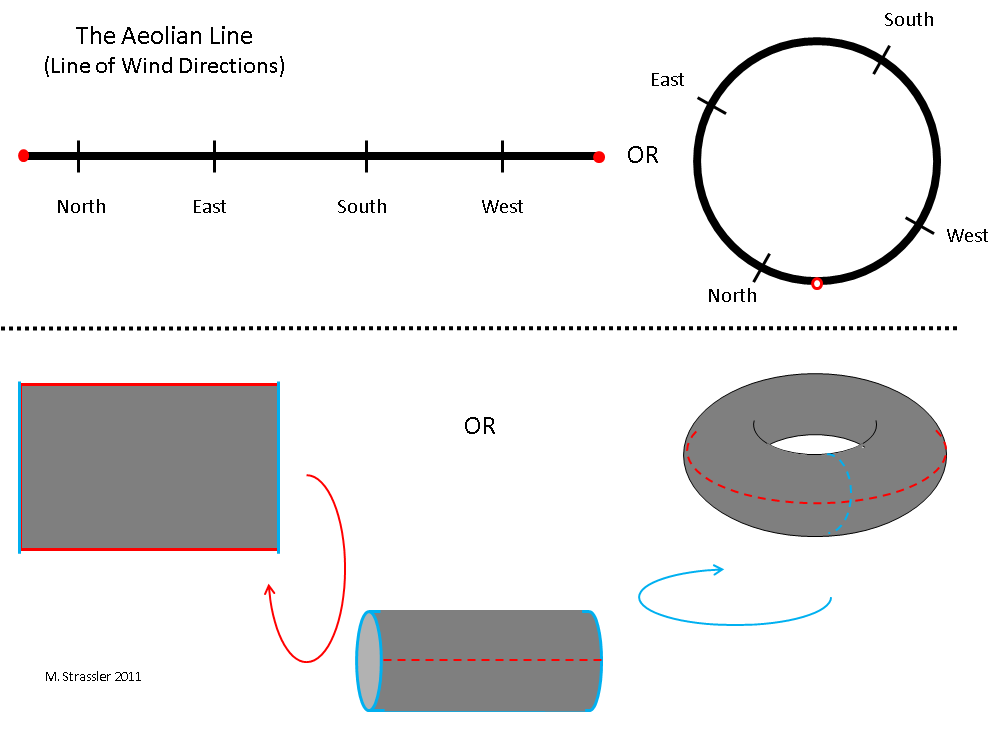
Fig. one
')
Yes, this is indeed an extremely important question, and the answer to it is necessary for understanding the spaces. Two images — a loop and a segment with two matching ends — indeed represent the same one-dimensional eolian line. The region surrounded by the loop is only a property of the representation we have chosen, and not a property of the aeolian line itself! We should not confuse the properties of the pictures used by us for visualization with the properties of the spaces! This is easy to do, but it is very important not to do it.
As another example, donut (torus) is shown, which seems to have internal and external parts. But it is not. Just as a circle can be represented by a segment with the left end coinciding with the right, so the torus can be represented as a rectangle, in which the top side coincides with the bottom and the left side with the right.
To check this, take a piece of paper. Connect the top edge with the bottom. You get a cylinder. Use imagination to bend the right and left ends so that they touch - and you will immediately see what a torus should make.
The rectangle with matching sides has no “inside” and “outside”, so the cylinder or torus does not have this either. In other words, the properties of space can be studied if you are traveling within it. To see that the circle has an interior and an outer part, you need to cross it: but if your circle is an eolian line, then it is impossible. Wind can not be asked to cross the circle from north to southeast. It can only move in a circle, across the east, or across the west. Only the line itself is inherent in the aeolian line!
Similarly, you can not ask the tightrope walker with rice. 6 articles about one-dimensional worlds to move from one part of a circular rope to another. The only safe option for his movement would be to go around the circle. Therefore, the wind or the tightrope walker cannot find out whether or not the circle has internal and external parts.
This concept is crucial for understanding the expansion of the universe. If you belong to the majority, you probably thought (as I did in my youth): “What is it expanding?” By asking this question, you made the same mistake that relates to a circle: you confused something expanding with the idea of something then expanding.
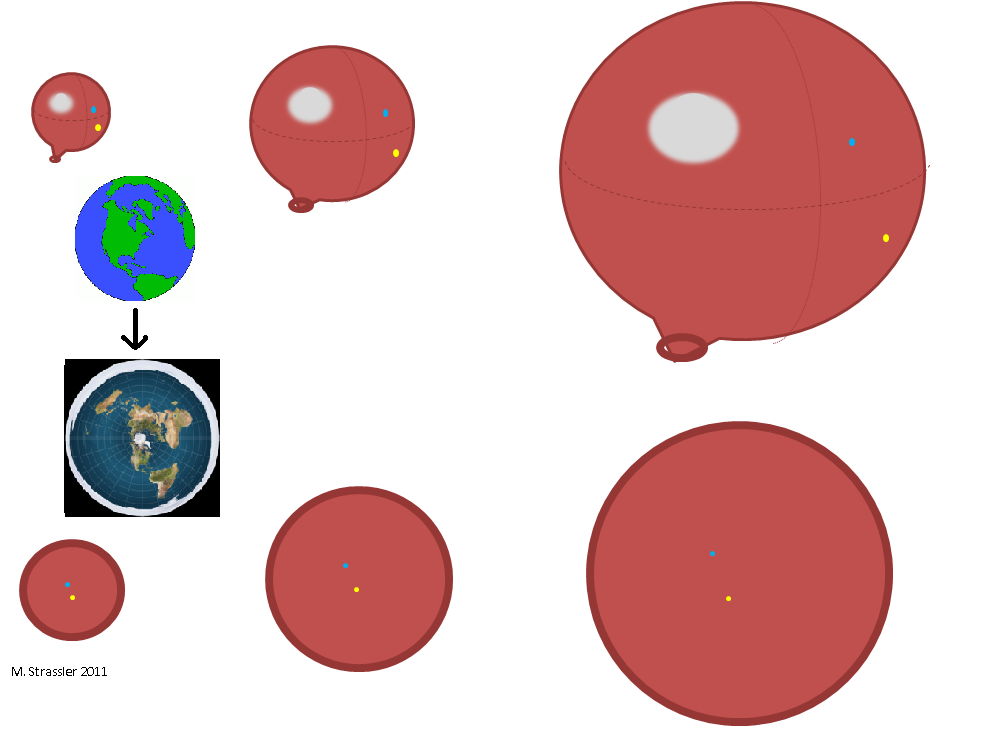
Fig. 2
For example, you can imagine an expanding ball. The ball looks to us as if it is expanding into a larger three-dimensional space in which it is located. But if you were an ant on a ball, you would not know anything about any inside and outside parts; you would only know that the space in which you are able to move has increased. You could even, being an ant cartographer, imagine this space in the form of a disk, whose edges are reduced to a single point (for example, to the point through which the ball is inflated). You would not think about “inside” and “outside”, you would only know that the distance between the yellow and blue dots (and between any pair of points on the ball) increases.
Another two-dimensional surface is the surface of the Earth itself. Suppose you woke up one morning, and the surface of the Earth doubled. You would not know whether the view of the Earth has changed for an observer from space, or whether the diameter of the Earth has grown. You would only be aware that taking a trip to work or grocery shopping takes longer than before.
The fact that the inner or outer part of the ball is a property of the representation of expanding space, and not of the space itself, is more obvious in an example with an infinite plane. The infinite plane may well expand, although it does not expand in anything. It fills the same space after expansion, as before it, just the distances between objects in space (for example, between the points shown in the figure) grow. The plane is essentially growing in size, but it is not inside a larger space, and therefore, obviously, it cannot expand into this larger space. It can simply expand, that's all.
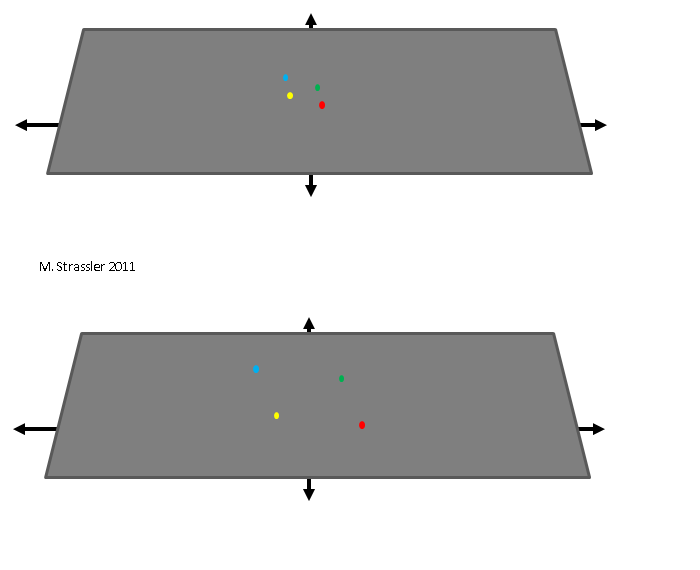
Fig. 3
So with the universe. As the plane just described, the space of the Universe simply expands. From the outside it is impossible to see, there is simply no “outside”. But the expansion of the universe can be determined, and being on the plane itself: the distance between any large objects of the universe (in particular, between galaxies, huge universe star cities) increases and increases as the universe expands. Over time, traveling from one galaxy to another will take more and more time. This is exactly what the Big Bang did: it took small areas of space and turned them into huge ones. It was not an explosion, it was not like a bomb explosion. This expansion of the space itself.
This sensible, but, at first glance, paradoxical question is simply incorrectly asked. These are the consequences of what you imagined are completely different. I will try to correct the course of your thoughts.
Let's go back and look at fig. 3 of the article about one-dimensional worlds . I reproduced the part of this figure we need in fig. 1 in this article. Pay attention to two completely different representations of the aeolian line (measurements of possible wind directions, which include such directions as north, southeast, west-north-west, etc.). One of the representations is a line segment, the left end of which coincides with the right. The other is a loop on the plane. Just a second, you say - they look different. The loop surrounds a specific area, it has an inner and outer part. There is no such segment. So how can they portray the same thing?

Fig. one
')
Yes, this is indeed an extremely important question, and the answer to it is necessary for understanding the spaces. Two images — a loop and a segment with two matching ends — indeed represent the same one-dimensional eolian line. The region surrounded by the loop is only a property of the representation we have chosen, and not a property of the aeolian line itself! We should not confuse the properties of the pictures used by us for visualization with the properties of the spaces! This is easy to do, but it is very important not to do it.
As another example, donut (torus) is shown, which seems to have internal and external parts. But it is not. Just as a circle can be represented by a segment with the left end coinciding with the right, so the torus can be represented as a rectangle, in which the top side coincides with the bottom and the left side with the right.
To check this, take a piece of paper. Connect the top edge with the bottom. You get a cylinder. Use imagination to bend the right and left ends so that they touch - and you will immediately see what a torus should make.
The rectangle with matching sides has no “inside” and “outside”, so the cylinder or torus does not have this either. In other words, the properties of space can be studied if you are traveling within it. To see that the circle has an interior and an outer part, you need to cross it: but if your circle is an eolian line, then it is impossible. Wind can not be asked to cross the circle from north to southeast. It can only move in a circle, across the east, or across the west. Only the line itself is inherent in the aeolian line!
Similarly, you can not ask the tightrope walker with rice. 6 articles about one-dimensional worlds to move from one part of a circular rope to another. The only safe option for his movement would be to go around the circle. Therefore, the wind or the tightrope walker cannot find out whether or not the circle has internal and external parts.
This concept is crucial for understanding the expansion of the universe. If you belong to the majority, you probably thought (as I did in my youth): “What is it expanding?” By asking this question, you made the same mistake that relates to a circle: you confused something expanding with the idea of something then expanding.

Fig. 2
For example, you can imagine an expanding ball. The ball looks to us as if it is expanding into a larger three-dimensional space in which it is located. But if you were an ant on a ball, you would not know anything about any inside and outside parts; you would only know that the space in which you are able to move has increased. You could even, being an ant cartographer, imagine this space in the form of a disk, whose edges are reduced to a single point (for example, to the point through which the ball is inflated). You would not think about “inside” and “outside”, you would only know that the distance between the yellow and blue dots (and between any pair of points on the ball) increases.
Another two-dimensional surface is the surface of the Earth itself. Suppose you woke up one morning, and the surface of the Earth doubled. You would not know whether the view of the Earth has changed for an observer from space, or whether the diameter of the Earth has grown. You would only be aware that taking a trip to work or grocery shopping takes longer than before.
The fact that the inner or outer part of the ball is a property of the representation of expanding space, and not of the space itself, is more obvious in an example with an infinite plane. The infinite plane may well expand, although it does not expand in anything. It fills the same space after expansion, as before it, just the distances between objects in space (for example, between the points shown in the figure) grow. The plane is essentially growing in size, but it is not inside a larger space, and therefore, obviously, it cannot expand into this larger space. It can simply expand, that's all.

Fig. 3
So with the universe. As the plane just described, the space of the Universe simply expands. From the outside it is impossible to see, there is simply no “outside”. But the expansion of the universe can be determined, and being on the plane itself: the distance between any large objects of the universe (in particular, between galaxies, huge universe star cities) increases and increases as the universe expands. Over time, traveling from one galaxy to another will take more and more time. This is exactly what the Big Bang did: it took small areas of space and turned them into huge ones. It was not an explosion, it was not like a bomb explosion. This expansion of the space itself.
Source: https://habr.com/ru/post/374165/
All Articles