Kaluza-Klein Partner Particles, Part 1
In this and the next article we will find out why the presence of additional dimensions leads to the emergence of Kaluza-Klein partner particles (described in the previous article of this series). If a particle of known type and mass m is able to move in an unknown dimension - an additional dimension - then we will inevitably discover many other types of particles, similar to those known to us, but heavier, with masses M> m.
In this article I will begin an explanation of why this is so, but I will give only half of the proof. This half will tell you about why there are KK-partners, and why they all have mass M> m. But this part of the proof would be incorrect to imply that for every mass M greater than m, there is a partner particle. And only in the second step, when we add a little quantum mechanics, we get the correct answer: these particles have a discrete set of certain masses, in which the first is somewhat (possibly much) heavier than the known.
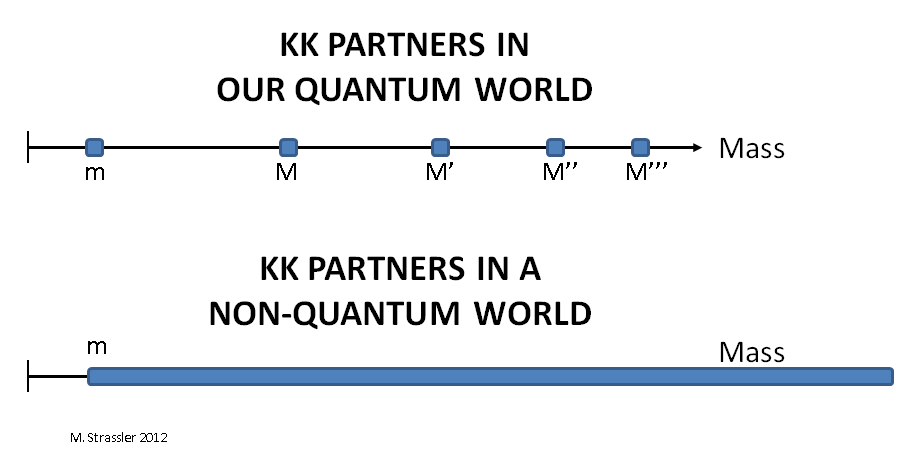
Fig. one
Let's start with the naive question about the strip - the ship channel from our previous examples . An observer such as a cargo ship from the example knows nothing about a short measurement, and considers that the channel is a line, not a strip. But if this observer has a scientific mind, he can guess something. Firstly, he knows about moving forward and backward along the strip; for him, speed and momentum are meaningful, directed along it. Secondly, he knows about energy and about the fact that it is connected with mass and motion. In particular, the energy of the particle E is related to its mass m and its motion (in particular, the momentum p along the strip) according to the well-known Einstein formula:
')
She says that the particle energy is given by a combination of mass energy and motion energy. For a stationary particle with no momentum (p = 0), this formula reduces to E 2 = m 2 c 4 , or, in other words, E = mc 2 .
So, if a small boat is in the channel without movement, an observer who knows both measurements will say about it: its momentum is zero, and the energy is derived from the mass E = mc 2 . And the observer, who knows only about the measurement along the strip, will say the same thing. See fig. 2, the upper third, where the point of view of the observer, who knows about two dimensions, is shown in the upper part, and the point of view of the observer, who knows only about one dimension, is indicated below.
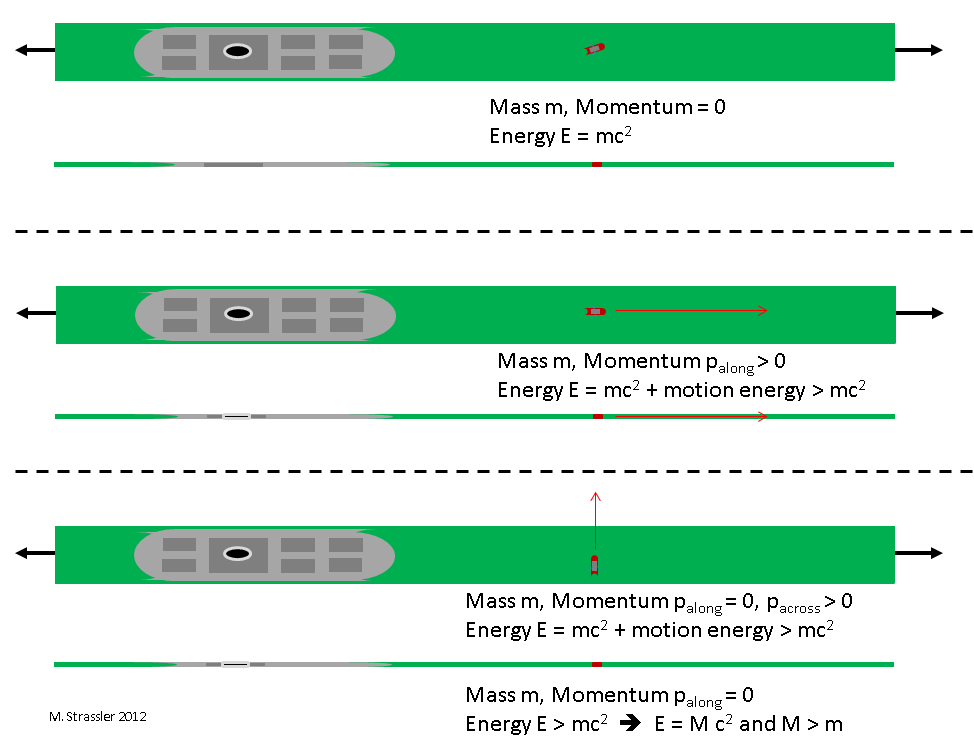
Fig. 2
If a small boat moves along a channel, then an observer who has an idea of both dimensions will say: its momentum along the channel p along non-zero, and the square of its energy is equal to
And an observer who knows only about one dimension will again say the same thing. See fig. 2, the middle part.
But what does the observer say, studying a particle moving not along a strip, but across? See fig. 2, lower third.
An observer who knows about two measurements will say: its impulse along channel p along zero, but impulse across channel p across non-zero, therefore the square of its energy will be equal
Note that this necessarily means that E> mc 2 , since the boat has both mass energy and motion energy.
However, an observer who knows only about one dimension will not be able to say the same thing, since he does not know anything about the possibility of p going across . He will think, looking at this particle, that it is not moving. After all, it does not move along the canal, but this observer is only able to catch such a movement. Therefore, according to the observer, all the energy of a particle, whatever it may be, must be attributed to its mass.
So looking at a particle with p along = 0 and a non-zero p across , the one-dimensional observer makes a mistake, albeit a rather interesting one. He says: hmm. The momentum of this object is zero, so its energy must be equal to its mass multiplied by c 2 , as was the case with the boat at the top of the picture. But its energy E is greater than mc 2 , therefore it cannot be the same boat that we saw at the top of the figure. Obviously, in nature there is another type of small boats, about which we did not know, similar to the first, but with a different, larger mass: M = E / c 2 .
In other words, if a boat of mass m moves with impulse p across the channel, the naive observer knows nothing about the extra dimension and makes an incorrect conclusion that he is observing a boat of mass M> m, s
Based on such reasoning, we get the correct information: a sign of the presence of an additional measurement in the presence of particles similar in nature to known particles (which move only along the strip), but seemingly heavier (due to their unobservable movement across the strip). This can be immediately generalized from the case of a strip (with one long and one short dimensions) to our Universe (with three long dimensions and, possibly, with one or more short ones). When known particles move in additional (unknown) dimensions, they seem to us heavier versions of themselves.
But the intuition we obtained from this data is also incorrect, because it can be concluded from them that a particle moving across the strip can have any momentum, and therefore, the observer must see particles with all possible masses M exceeding m, as shown below. 1. And it is not. Instead, only certain values of the masses M are possible, as shown at the top of Fig. 1 is a discrete set, not a continuous set of particles, which would follow from our reasoning. All because of quantum mechanics. Due to the fact that the “particles” are actually quantizing waves, quanta, which was not the case for the small boat from our example. In the next article we will see where this difference comes from.
In this article I will begin an explanation of why this is so, but I will give only half of the proof. This half will tell you about why there are KK-partners, and why they all have mass M> m. But this part of the proof would be incorrect to imply that for every mass M greater than m, there is a partner particle. And only in the second step, when we add a little quantum mechanics, we get the correct answer: these particles have a discrete set of certain masses, in which the first is somewhat (possibly much) heavier than the known.

Fig. one
Let's start with the naive question about the strip - the ship channel from our previous examples . An observer such as a cargo ship from the example knows nothing about a short measurement, and considers that the channel is a line, not a strip. But if this observer has a scientific mind, he can guess something. Firstly, he knows about moving forward and backward along the strip; for him, speed and momentum are meaningful, directed along it. Secondly, he knows about energy and about the fact that it is connected with mass and motion. In particular, the energy of the particle E is related to its mass m and its motion (in particular, the momentum p along the strip) according to the well-known Einstein formula:
')
She says that the particle energy is given by a combination of mass energy and motion energy. For a stationary particle with no momentum (p = 0), this formula reduces to E 2 = m 2 c 4 , or, in other words, E = mc 2 .
So, if a small boat is in the channel without movement, an observer who knows both measurements will say about it: its momentum is zero, and the energy is derived from the mass E = mc 2 . And the observer, who knows only about the measurement along the strip, will say the same thing. See fig. 2, the upper third, where the point of view of the observer, who knows about two dimensions, is shown in the upper part, and the point of view of the observer, who knows only about one dimension, is indicated below.

Fig. 2
If a small boat moves along a channel, then an observer who has an idea of both dimensions will say: its momentum along the channel p along non-zero, and the square of its energy is equal to
And an observer who knows only about one dimension will again say the same thing. See fig. 2, the middle part.
But what does the observer say, studying a particle moving not along a strip, but across? See fig. 2, lower third.
An observer who knows about two measurements will say: its impulse along channel p along zero, but impulse across channel p across non-zero, therefore the square of its energy will be equal
Note that this necessarily means that E> mc 2 , since the boat has both mass energy and motion energy.
However, an observer who knows only about one dimension will not be able to say the same thing, since he does not know anything about the possibility of p going across . He will think, looking at this particle, that it is not moving. After all, it does not move along the canal, but this observer is only able to catch such a movement. Therefore, according to the observer, all the energy of a particle, whatever it may be, must be attributed to its mass.
So looking at a particle with p along = 0 and a non-zero p across , the one-dimensional observer makes a mistake, albeit a rather interesting one. He says: hmm. The momentum of this object is zero, so its energy must be equal to its mass multiplied by c 2 , as was the case with the boat at the top of the picture. But its energy E is greater than mc 2 , therefore it cannot be the same boat that we saw at the top of the figure. Obviously, in nature there is another type of small boats, about which we did not know, similar to the first, but with a different, larger mass: M = E / c 2 .
In other words, if a boat of mass m moves with impulse p across the channel, the naive observer knows nothing about the extra dimension and makes an incorrect conclusion that he is observing a boat of mass M> m, s
Based on such reasoning, we get the correct information: a sign of the presence of an additional measurement in the presence of particles similar in nature to known particles (which move only along the strip), but seemingly heavier (due to their unobservable movement across the strip). This can be immediately generalized from the case of a strip (with one long and one short dimensions) to our Universe (with three long dimensions and, possibly, with one or more short ones). When known particles move in additional (unknown) dimensions, they seem to us heavier versions of themselves.
But the intuition we obtained from this data is also incorrect, because it can be concluded from them that a particle moving across the strip can have any momentum, and therefore, the observer must see particles with all possible masses M exceeding m, as shown below. 1. And it is not. Instead, only certain values of the masses M are possible, as shown at the top of Fig. 1 is a discrete set, not a continuous set of particles, which would follow from our reasoning. All because of quantum mechanics. Due to the fact that the “particles” are actually quantizing waves, quanta, which was not the case for the small boat from our example. In the next article we will see where this difference comes from.
Source: https://habr.com/ru/post/374143/
All Articles