Quantum tunneling process
I will begin with two simple questions with fairly intuitive answers. Take the bowl and the ball (Fig. 1). If I need to:
• the ball remained stationary after I placed it in the bowl, and
• it remained at about the same position as you moved the bowl,
then where should I put it?
')

Fig. one
Of course, I need to put it in the center, at the very bottom. Why? It is intuitively clear that if I put it somewhere else, it will sink to the bottom and dangle to and fro. As a result, the friction will reduce the height of the rattling and slow it down.
In principle, you can try to balance the ball on the edge of the bowl. But if I shake it a little, the ball will lose its balance and fall. So this place does not satisfy the second criterion in my question.
Let us call the position in which the ball remains motionless, and from which it does not strongly deviate with small movements of the bowl or ball, “stable position of the ball”. The bottom of the bowl is such a stable position.
Another question. If I have two bowls, as in fig. 2, where are the stable positions for the ball? It is also simple: there are two such places, namely, at the bottom of each of the bowls.
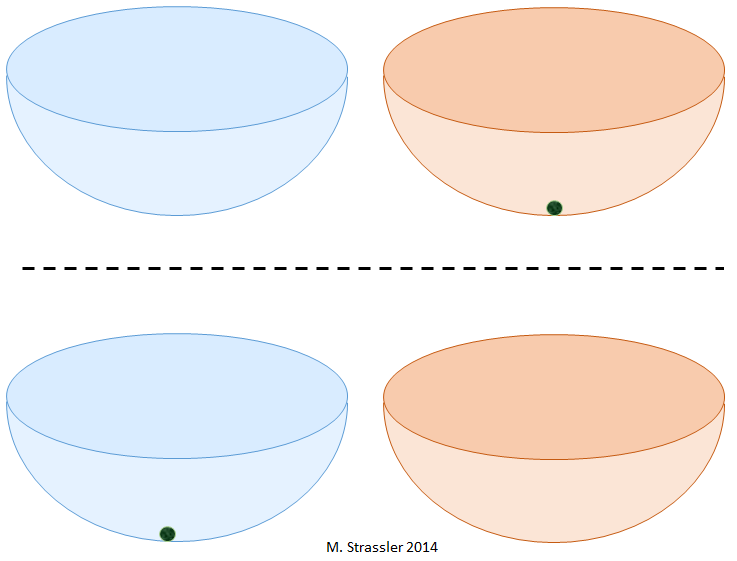
Fig. 2
Finally, another question with an intuitive answer. If I place the ball at the bottom of Bowl 1, and then leave the room, close it, I guarantee that no one will go there, check that there are no earthquakes and other shocks in this place, then what are the chances that after ten years re-open the room, I will find the ball at the bottom of the bowl 2? Of course, zero. In order for the ball to move from the bottom of bowl 1 to the bottom of bowl 2, someone or something must pick up the ball and move it from place to place, above the edge of bowl 1, toward the bowl 2 and then above the edge of bowl 2. Obviously, the ball will remain at the bottom of the bowl 1.
Obviously and essentially true. And yet, in the quantum world in which we live, not a single object remains truly immobile, and its position is not precisely known. So none of these answers are 100% correct.
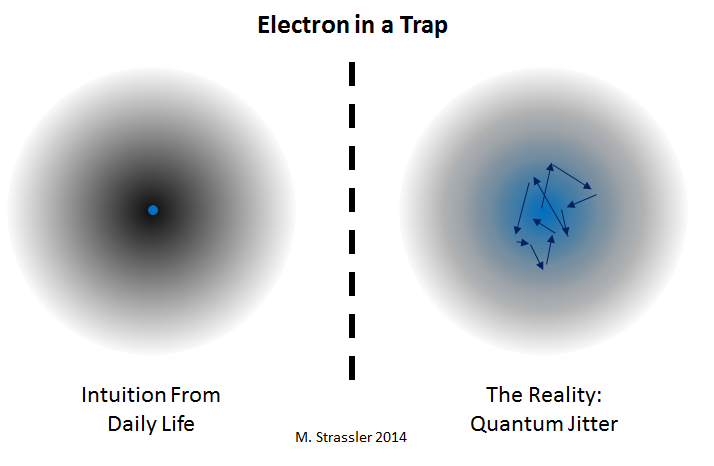
Fig. 3
If I place an elementary particle like an electron in a magnetic trap (Fig. 3) working like a bowl, tending to push an electron to the center in the same way as gravity and the walls of the bowl push the ball to the center of the bowl in fig. 1, then what will be the stable position of the electron? As it should have been intuitively expected, the average position of the electron will be stationary only if it is placed in the center of the trap.
But quantum mechanics adds one nuance. The electron cannot remain motionless; his position is subject to "quantum jitter". Because of this, his position and movement is constantly changing, or even has some degree of uncertainty (it works the famous "principle of uncertainty"). Only the middle position of the electron is in the center of the trap; if you look at the electron, it will be somewhere else in the trap, near the center, but not quite there. The electron is stationary only in this sense: it usually moves, but its movement is random, and since it is trapped, on average it does not move anywhere.
This is a bit strange, but just reflects the fact that the electron is not what you think, and does not behave like any of the objects you have seen.
This, by the way, also ensures that the electron cannot be balanced at the edge of the trap, unlike the ball at the edge of the bowl (as below in Fig. 1). The position of the electron is not determined precisely, therefore it cannot be exactly balanced; therefore, even without shaking the trap, the electron will lose balance and will almost immediately fall through.
But what is more strange is the case when I will have two traps separated from each other, and I will place an electron in one of them. Yes, the center of one of the traps is a good, stable position for an electron. This is so - in the sense that the electron can remain there and not run away if you shake the trap.
However, if you place the electron in trap No. 1, and leave, close the room, etc., there is a certain probability (Fig. 4) that when I return, the electron will be trapped in No. 2.
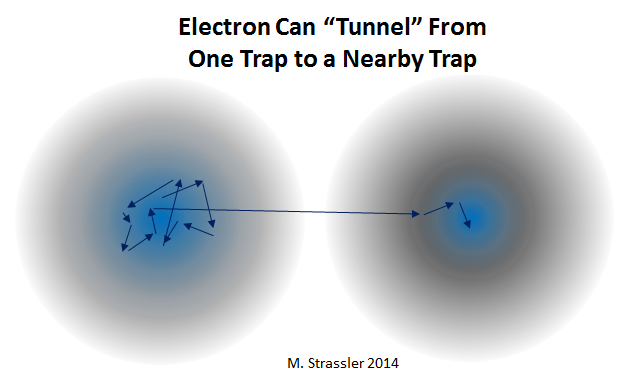
Fig. four
How did he do it? If you imagine electrons in the form of balls, you will not understand this. But electrons are not like balls (or at least your intuitive idea about balls), and their quantum jitter gives them an extremely small, but non-zero chance to “pass through walls” —a seemingly incredible opportunity to move to the other side. This is called tunneling - but do not think that the electron digs a hole in the wall. And you can never catch it in the wall - so to speak, in the act. Just the wall is not completely impenetrable for such things as an electron; electrons cannot be so easily trapped.
Actually, it's still crazier: since it's true for an electron, it's true for a ball in a vase. The ball can be in vase 2, if you wait long enough. But the probability of this is extremely small. So small that even if you wait a billion years, or even billions of billions of billions of years, this will not be enough. From a practical point of view, this "never" will not happen.
Our world is quantum, and all objects consist of elementary particles and obey the rules of quantum physics. Quantum jitter is always present. But most of the objects whose mass is large compared to the mass of elementary particles — a ball, for example, or even a speck of dust — are quantum jitter too small to detect, except for specially designed experiments. And the next possibility to tunnel through walls is also not observed in everyday life.
In other words: any object can tunnel through the wall, but the probability of this usually decreases sharply if:
• the object has a large mass,
• the wall is thick (long distance between two sides),
• the wall is difficult to overcome (to pierce the wall, you need a lot of energy).
In principle, the ball can overcome the edge of the bowl, but in practice this may not be possible. An electron can easily escape from a trap if the traps are close and not very deep, but it can be very difficult if they are far and very deep.

Fig. five
Or maybe this tunneling is just a theory? Definitely not. It is fundamental to chemistry, occurs in many materials, plays a role in biology, and this is the principle used in our most cunning and powerful microscopes.
For brevity, let me focus on a microscope. In fig. Figure 5 shows an image of atoms made with a scanning tunneling microscope . Such a microscope has a narrow needle, whose tip moves in close proximity to the material under study (see Fig. 6). The material and the needle, of course, consist of atoms; and there are electrons on the outskirts of the atoms. Roughly speaking, electrons are trapped inside the material under study or at the tip of a microscope. But the closer the tip to the surface, the more likely the tunneling transition of electrons between them. A simple device (the potential difference is maintained between the material and the needle) ensures that electrons prefer to jump from surface to needle, and this flow is an electric current that can be measured. The needle moves above the surface, and the surface is closer and farther from the tip, and the current changes - it becomes stronger with decreasing distance and weaker with increasing. By tracking the current (or, conversely, moving the needle up and down to maintain a constant current) while scanning the surface, the microscope makes a conclusion about the shape of this surface, and often there is enough detail to see the individual atoms.
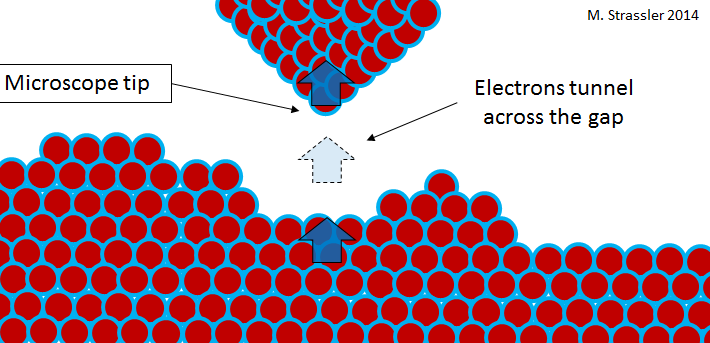
Fig. 6
Tunneling plays many other roles in nature and modern technology.
In fig. 4 I meant that both traps had the same depth - just like the two bowls in fig. 2 same shape. This means that the electron, being in any of the traps, with the same probability will jump to another.
Now suppose that one electron trap in fig. 4 deeper than the other - just as if one bowl in fig. 2 was deeper than the other (see Fig. 7). Although an electron can tunnel in any direction, it will be much easier for it to tunnel from a shallower to a deeper trap than vice versa. Accordingly, if we wait long enough for the electron to have enough time to tunnel in any direction and return, and then start taking measurements to determine its location, we will most often find it in a deep trap. (In fact, there are some nuances here too; everything also depends on the shape of the trap). However, the depth difference does not have to be large in order for tunneling from a deeper to a shallower trap to become extremely rare.
In short, tunneling in general will occur in both directions, but the probability of transition from a shallow to a deep trap is much greater.
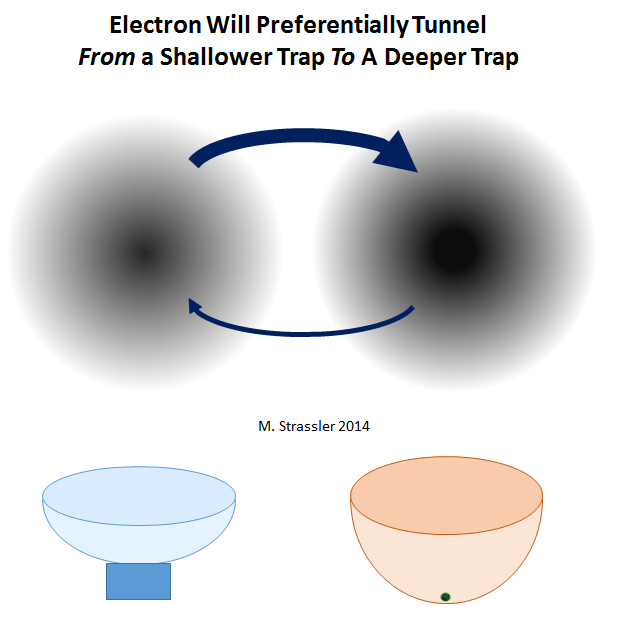
Fig. 7
It is this feature that is used in a scanning tunneling microscope to ensure that electrons move only in one direction. In fact, the tip of the microscope needle turns out to be a deeper trap than the surface under study, therefore electrons prefer to tunnel from the surface to the needle, and not vice versa. But the microscope will work in the opposite case. Traps are made deeper or smaller with the help of a power source that creates a potential difference between the needle and the surface, which creates a difference in the energies of the electrons on the needle and electrons on the surface. Because making electrons more likely to tunnel in one direction than another, is quite simple, this tunneling becomes practically useful for use in electronics.
• the ball remained stationary after I placed it in the bowl, and
• it remained at about the same position as you moved the bowl,
then where should I put it?
')

Fig. one
Of course, I need to put it in the center, at the very bottom. Why? It is intuitively clear that if I put it somewhere else, it will sink to the bottom and dangle to and fro. As a result, the friction will reduce the height of the rattling and slow it down.
In principle, you can try to balance the ball on the edge of the bowl. But if I shake it a little, the ball will lose its balance and fall. So this place does not satisfy the second criterion in my question.
Let us call the position in which the ball remains motionless, and from which it does not strongly deviate with small movements of the bowl or ball, “stable position of the ball”. The bottom of the bowl is such a stable position.
Another question. If I have two bowls, as in fig. 2, where are the stable positions for the ball? It is also simple: there are two such places, namely, at the bottom of each of the bowls.

Fig. 2
Finally, another question with an intuitive answer. If I place the ball at the bottom of Bowl 1, and then leave the room, close it, I guarantee that no one will go there, check that there are no earthquakes and other shocks in this place, then what are the chances that after ten years re-open the room, I will find the ball at the bottom of the bowl 2? Of course, zero. In order for the ball to move from the bottom of bowl 1 to the bottom of bowl 2, someone or something must pick up the ball and move it from place to place, above the edge of bowl 1, toward the bowl 2 and then above the edge of bowl 2. Obviously, the ball will remain at the bottom of the bowl 1.
Obviously and essentially true. And yet, in the quantum world in which we live, not a single object remains truly immobile, and its position is not precisely known. So none of these answers are 100% correct.
Tunneling

Fig. 3
If I place an elementary particle like an electron in a magnetic trap (Fig. 3) working like a bowl, tending to push an electron to the center in the same way as gravity and the walls of the bowl push the ball to the center of the bowl in fig. 1, then what will be the stable position of the electron? As it should have been intuitively expected, the average position of the electron will be stationary only if it is placed in the center of the trap.
But quantum mechanics adds one nuance. The electron cannot remain motionless; his position is subject to "quantum jitter". Because of this, his position and movement is constantly changing, or even has some degree of uncertainty (it works the famous "principle of uncertainty"). Only the middle position of the electron is in the center of the trap; if you look at the electron, it will be somewhere else in the trap, near the center, but not quite there. The electron is stationary only in this sense: it usually moves, but its movement is random, and since it is trapped, on average it does not move anywhere.
This is a bit strange, but just reflects the fact that the electron is not what you think, and does not behave like any of the objects you have seen.
This, by the way, also ensures that the electron cannot be balanced at the edge of the trap, unlike the ball at the edge of the bowl (as below in Fig. 1). The position of the electron is not determined precisely, therefore it cannot be exactly balanced; therefore, even without shaking the trap, the electron will lose balance and will almost immediately fall through.
But what is more strange is the case when I will have two traps separated from each other, and I will place an electron in one of them. Yes, the center of one of the traps is a good, stable position for an electron. This is so - in the sense that the electron can remain there and not run away if you shake the trap.
However, if you place the electron in trap No. 1, and leave, close the room, etc., there is a certain probability (Fig. 4) that when I return, the electron will be trapped in No. 2.

Fig. four
How did he do it? If you imagine electrons in the form of balls, you will not understand this. But electrons are not like balls (or at least your intuitive idea about balls), and their quantum jitter gives them an extremely small, but non-zero chance to “pass through walls” —a seemingly incredible opportunity to move to the other side. This is called tunneling - but do not think that the electron digs a hole in the wall. And you can never catch it in the wall - so to speak, in the act. Just the wall is not completely impenetrable for such things as an electron; electrons cannot be so easily trapped.
Actually, it's still crazier: since it's true for an electron, it's true for a ball in a vase. The ball can be in vase 2, if you wait long enough. But the probability of this is extremely small. So small that even if you wait a billion years, or even billions of billions of billions of years, this will not be enough. From a practical point of view, this "never" will not happen.
Our world is quantum, and all objects consist of elementary particles and obey the rules of quantum physics. Quantum jitter is always present. But most of the objects whose mass is large compared to the mass of elementary particles — a ball, for example, or even a speck of dust — are quantum jitter too small to detect, except for specially designed experiments. And the next possibility to tunnel through walls is also not observed in everyday life.
In other words: any object can tunnel through the wall, but the probability of this usually decreases sharply if:
• the object has a large mass,
• the wall is thick (long distance between two sides),
• the wall is difficult to overcome (to pierce the wall, you need a lot of energy).
In principle, the ball can overcome the edge of the bowl, but in practice this may not be possible. An electron can easily escape from a trap if the traps are close and not very deep, but it can be very difficult if they are far and very deep.
And exactly tunneling happens?

Fig. five
Or maybe this tunneling is just a theory? Definitely not. It is fundamental to chemistry, occurs in many materials, plays a role in biology, and this is the principle used in our most cunning and powerful microscopes.
For brevity, let me focus on a microscope. In fig. Figure 5 shows an image of atoms made with a scanning tunneling microscope . Such a microscope has a narrow needle, whose tip moves in close proximity to the material under study (see Fig. 6). The material and the needle, of course, consist of atoms; and there are electrons on the outskirts of the atoms. Roughly speaking, electrons are trapped inside the material under study or at the tip of a microscope. But the closer the tip to the surface, the more likely the tunneling transition of electrons between them. A simple device (the potential difference is maintained between the material and the needle) ensures that electrons prefer to jump from surface to needle, and this flow is an electric current that can be measured. The needle moves above the surface, and the surface is closer and farther from the tip, and the current changes - it becomes stronger with decreasing distance and weaker with increasing. By tracking the current (or, conversely, moving the needle up and down to maintain a constant current) while scanning the surface, the microscope makes a conclusion about the shape of this surface, and often there is enough detail to see the individual atoms.

Fig. 6
Tunneling plays many other roles in nature and modern technology.
Tunneling between traps of different depths
In fig. 4 I meant that both traps had the same depth - just like the two bowls in fig. 2 same shape. This means that the electron, being in any of the traps, with the same probability will jump to another.
Now suppose that one electron trap in fig. 4 deeper than the other - just as if one bowl in fig. 2 was deeper than the other (see Fig. 7). Although an electron can tunnel in any direction, it will be much easier for it to tunnel from a shallower to a deeper trap than vice versa. Accordingly, if we wait long enough for the electron to have enough time to tunnel in any direction and return, and then start taking measurements to determine its location, we will most often find it in a deep trap. (In fact, there are some nuances here too; everything also depends on the shape of the trap). However, the depth difference does not have to be large in order for tunneling from a deeper to a shallower trap to become extremely rare.
In short, tunneling in general will occur in both directions, but the probability of transition from a shallow to a deep trap is much greater.

Fig. 7
It is this feature that is used in a scanning tunneling microscope to ensure that electrons move only in one direction. In fact, the tip of the microscope needle turns out to be a deeper trap than the surface under study, therefore electrons prefer to tunnel from the surface to the needle, and not vice versa. But the microscope will work in the opposite case. Traps are made deeper or smaller with the help of a power source that creates a potential difference between the needle and the surface, which creates a difference in the energies of the electrons on the needle and electrons on the surface. Because making electrons more likely to tunnel in one direction than another, is quite simple, this tunneling becomes practically useful for use in electronics.
Source: https://habr.com/ru/post/374055/
All Articles