Chaos eliminates the need for the Multiverse.

Scientists are exploring the universe and see an amazing structure. It contains fantastically complex objects and processes. Every event in the universe follows the exact laws of nature, ideally expressed in the language of mathematics. These laws seem to us to be finely tuned in order for life to emerge, and, in particular, intelligent life. What are these laws of nature and how can we find them?

The universe is so well structured and streamlined that we compare it with the most complex and accurate inventions of its time. In the 18th and 19th centuries, the Universe was compared to ideally operating clocks. The philosophers then discussed the Watchmaker. In the XX and XXI centuries, the most complex object is a computer. The universe is compared with a perfectly running supercomputer . Researchers wonder: how was this computer programmed?
')
How can this whole structure be explained? Why do laws seem perfectly tuned to the emergence of life, and why are they expressed in such exact mathematical language? Is the universe really as structured as it seems?



One of the answers to these questions is Platonism (or its cousin, realism ). It is a belief that the laws of nature are objective and have always existed. They have the exact and ideal form that exists in the world of Plato. These laws work perfectly, and they have formed the Universe that we are observing. They not only exist in this world, but also live alongside perfect mathematics. This should help explain why laws are written in the language of mathematics.

Platonism leaves much to be desired, and a lot. The main problem of platonism is metaphysics, not science. But even if we accept it, many questions still remain. Why in the platonic world there are laws that generate intelligent life in the universe, and not some other? How did this platonic attic appear? Why does the physical universe follow the ephemeral rules? How can scientists and mathematicians gain access to Plato's treasure chest in the form of exact ideals?

The Multiverse is another answer that has recently become quite fashionable. This theory is an attempt to explain why there are laws in our Universe that give life. A believer in the Multiverse claims that our universe is just one of many. Each universe has its own set of rules and its possible structures corresponding to them. Physicists who are promoting the theory of the multiverse believe that the laws in each universe add up randomly. In our universe, we see livable structures because we are lucky to live in one of the few universes in which there are such laws. And although the Multiverse explains some of the structures we see, some questions remain open. Instead of asking why the universe has such structures, we can ask why the Multiverse has such structures. Another problem: if the Multiverse answers some of our questions, then who said that it exists? Since the majority believes that we have no connection with other universes, the question of the existence of the Multiverse remains in the field of metaphysics.

There is another, more interesting, explanation of the structure of the laws of nature. Instead of saying that the Universe is very structured, say that the Universe is chaotic, and for the most part there is no structure. And the reason why we see structures is that scientists work like a sieve; they focus only on those phenomena that have a structure and that can be predicted. They do not consider all phenomena. Instead, they choose only those that they can handle.

Some people will say that science studies all physical phenomena. This is not true. Who will win the next US presidential election and move to the White House is a physical question, but no scientist will look for the exact answer to it. Whether or not a computer will stop working with certain input data is a physical question, and yet we learn from Alan Turing that it is impossible to answer it. Scientists gave a classification of the general textures and heights of various types of clouds, but in general they are not at all interested in the exact shape of the cloud. Although its form is a physical phenomenon, scientists do not even try to study it. Science does not study all phenomena. Science studies predictable physical phenomena. This is almost a tautology: science predicts predictable phenomena.

Scientists have described the criterion for the phenomena that they decided to study: it is called symmetry. Symmetry is a property according to which, despite the change of something, there remains some fixed part. When we say that a face has symmetry, we mean that if you reflect the left side and replace it with the right one, it will look the same. When physicists use the word "symmetry," they discuss sets of physical phenomena. A set of phenomena has symmetry, if after some change it remains the same. The most obvious example is location symmetry. This means that if you conduct the same experiment in two different places, the results should be the same. The symmetry of time means that the results of experiments should not depend on when the experiment was conducted. There are many other types of symmetry.

Phenomena selected by scientists for research should have many different types of symmetries. When a physicist sees many phenomena, he must first determine whether they have symmetry. He conducts experiments in different places and at different times. If he achieves the same results, he then studies them in search of the root cause. If the experiments were asymmetric, he ignores them.

And although such scientists as Galileo and Newton saw symmetry in physical phenomena, all the power of symmetry was first investigated by Albert Einstein. He stated that the laws of physics must remain the same, even if the experimenter moves at a speed close to the speed of light. Mindful of this symmetry, he was able to create the laws of the special theory of relativity. Einstein was the first to understand that symmetry is the defining characteristic of physics. What has symmetry, it will be the law of nature. And the rest does not belong to science.

Shortly after Einstein showed the vital importance of symmetry to science, Emmy Noether proved a powerful theorem that determined the connection between symmetry and conservation laws. It is connected with the constants of nature, the central part of modern physics. Again, in the presence of symmetry there will be both conservation laws and constants. The physicist must be a sieve, and study phenomena that possess symmetry, allowing those phenomena that do not possess symmetry, to slip through fingers.

There are several problems with this explanation of the structures existing in the universe. For example, it seems that the phenomena chosen by us, possessing the laws of nature, give rise to all other phenomena. All the laws of particle physics, gravity and quantum theory have symmetries, and they are all studied by physicists. It seems that all phenomena originate from these theories, even those that do not possess symmetry. So, although the definition of the next US president is beyond the scope of science, this phenomenon will be determined by sociology, which is defined by psychology, which is determined by neuroscience, which depends on chemistry, which depends on particle physics and quantum mechanics. Determining an election winner is too difficult for scientists, but the election results depend on the laws of physics that are part of science.

Despite the fact that we could not explain the structure of the laws of nature, we believe that this is the best candidate for a solution. This is one of those decisions that do not include any metaphysical principles or the existence of a multitude of invisible universes. We do not need to look beyond the Universe in search of the cause of the structure inside it. We only need to look at how we view phenomena.

Before we continue, it is necessary to indicate that our solution has a property in common with the solution associated with the Multiverse. We postulated that for the most part the Universe is chaotic and there is no special structure in it. We just focus on a small number of existing structures. In the same way, those who believe in the Multiverse believe that most of them lack the structure for the formation of intelligent life. Only in a small number of chosen universes can complex structures be found. And we, the population of this complex universe, focus on these rare structures. Both solutions consist of concentrating on a small volume of structure, which is part of a huge chaotic whole.

The hierarchy of numerical systems

The idea that we see structure only because we select a subset of phenomena is new and difficult to understand. There is a similar situation in mathematics which is much easier to understand. We will focus on one important example in which the selection process is clearly visible. First we need to take a short tour through several numerical systems and their properties.

Consider real numbers. In one of the high schools, the teacher draws a line of real numbers on the blackboard and claims that it contains all the numbers you will ever need. If we take two real numbers, we will be able to add, subtract, multiply and divide them. They consist of a numerical system used in all aspects of science. Real numbers have one important property: they are ordered. of any two different real numbers, one will be greater than the other. Imagine a numerical line: from two different points one will be to the right of the other. This property is so obvious that it is rarely spoken of.


Emmy Noether

And although real numbers seem to be a complete picture, the story does not end there. Already in the XVI century, mathematicians began the search for more complex numerical systems. They began to work with the "imaginary" number i, a property of which is such that its square is -1. This clearly contrasts with any real number whose square is always positive. They identified the imaginary number as the product of a real number and i. Mathematicians defined the complex number as the sum of the real and imaginary. If r ₁ and r ₂ are real numbers, then r ₁ + r ₂ i is a complex number. Since a complex number consists of two real numbers, we draw them on a two-dimensional plane. The line of real numbers is on the complex plane. This corresponds to the fact that each real number r ₁ can be considered as a complex r ₁ + 0i (the number itself plus the zero complex term).

We know how to add, subtract, multiply, and divide complex numbers. However, they have one unusual property. Unlike real numbers, complex numbers are not ordered. Which of the two complex numbers, say 3 + 7.2i and 6 - 4i, is greater, and which is less? There is no obvious answer. In principle, of course, complex numbers can be ordered, but this ordering will not correspond to their multiplication). The fact that complex numbers are not ordered means that we lose structure when moving from real to complex numbers.

But the story does not end with complex numbers. In the same way as complex numbers can be made up of real numbers, quaternions can be made up of complex pairs. Let c ₁ = r ₁ + r ₂ i and c ₂ = r ₃ + r ₄ i be complex numbers. Then you can define a quaternion as q = c ₁ + c ₂ j, where j is a special number. It turns out that any quaternion can be written as

r ₁ + r ₂ i + r ₃ j + r ₄ k

where i, j and k are special numbers similar to complex numbers (ijk = -1 = i ² = j ² = k ² ). So if complex numbers consist of two real numbers, then quaternions consist of four real numbers. Each complex number r ₁ + r ₂ i can be considered as a special type of quaternion: r ₁ + r ₂ i + 0j + 0k. We can imagine quaternions as a four-dimensional space, two-dimensional subset of which are complex numbers. It is quite difficult for us, people, to visualize high order spaces.

Quaternions - a full numerical system. They can be easily added, subtracted, multiplied and divided. Like complex numbers, they cannot be ordered. And they have even less structure than complex numbers. If the multiplication of complex numbers is commutative, that is, for any complex numbers c ₁ and c _2, c ₁ c ₂ = c ₂ c ₁ , this is not true for all quaternions. This means that there are quaternions q ₁ and q ₂ such that q ₁ q ₂ does not equal q ₂ q ₁ .

This process of doubling a numerical system with a new special number is called the Cayley-Dixon procedure in honor of the mathematicians Arthur Cayley and Leonard Dixon. For a certain type of numerical system, it is possible to construct another numerical system with a dimension twice as large as the initial one. The new system is worse structured (it has less axioms) than the original one.

Applying the Cayley-Dixon procedure to quaternions, we obtain a numerical octonion system. This is an eight-dimensional number system. This means that each of the windows can be written in eight real numbers, as

r ₁ + r ₂ i + r ₃ j + r ₄ k + r ₅ l + r ₆ m + r ₇ n + r ₈ p

Although these actions are quite complex, we know how to add, subtract, multiply, and divide octonions. Each quaternion can be written as a special type of octonion, in which the last four coefficients are zero.

Like quaternions, octonions are neither ordered nor commutative. However, octonions are not yet associative. All previous numerical systems considered were associative. This means that for any three elements, a, b, and c, the two ways of multiplying them, a (bc) and (ab) c, are identical. However, this is not the case for the Octonions. There are octonions o1, o2 and o3 such that o1 (o2o3) (o1o2) o3.

We can continue this doubling and get an even larger, 16-dimensional numerical system, called sedenions . To describe it, you need 16 real numbers. Octonions are a special type of sedenion, in which the last eight coefficients are zero. But researchers shy away sedenion, because they have lost an important property. Although they can be added, subtracted and multiplied, there is no way to divide them. Most physicists believe that this is outside of "honest" mathematics. Even mathematicians find it difficult to handle them. You can make a 32-dimensional numerical system, and 64-dimensional, and so on. But they are usually not talked about, because so far they have very few uses. We will concentrate on the octonions. Summarize all numerical systems using this Venn diagram:



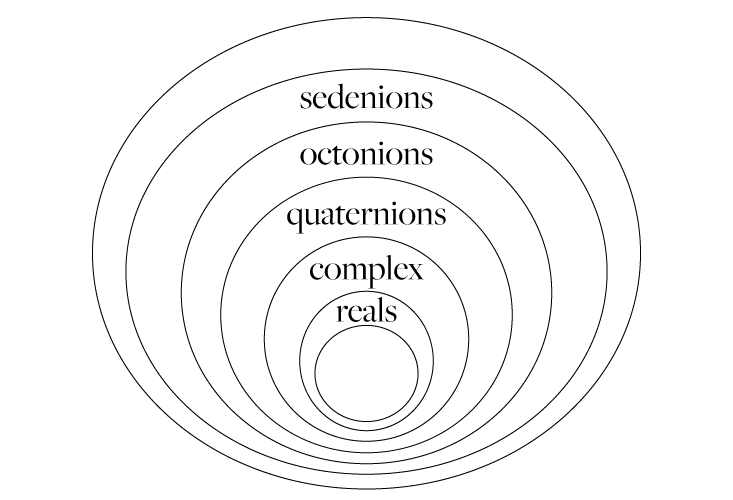
Let us discuss the applicability of these numerical systems. Real numbers are used in all areas of physics. All values, measurements, lengths of physical objects or processes are given in the form of real numbers. Although complex numbers were formulated by mathematicians to help solve equations (i is the solution to equation x ² = -1), physicists began using complex numbers to discuss waves in the middle of the 19th century. In the 20th century, complex numbers became the basis for research in quantum mechanics. Now complex numbers play an important role in various areas of physics. Quaternions appear in physics, but do not play important roles. Octonions, sedenions, and even large number systems rarely appear in the physical literature.

We discover the laws of mathematics

The usual approach to considering these numerical systems is that real numbers are fundamental, and complex, quaternions and octonions are strange, larger sets that help mathematicians and physicists to do something. Larger number systems are considered something unimportant and uninteresting.

Let's turn this approach upside down. Instead of considering the real numbers to be central, and the octonions to be a strange larger numerical system, let us imagine that the octonions are fundamental, and other numerical systems are simply subsets of the octonions. The only existing numerical system is the octonions. Paraphrasing Leopold Kronecker: “God created octonions, everything else is the work of man” [Kronecker said: “God created whole numbers, everything else is the work of man” / approx. trans.]. The octonions contain all the numbers we need. (In this case, as was shown earlier, we can do the same trick with sedenions and even with 64-dimensional numerical systems. But we will convey our ideas with the help of octonions).

Let's see how you can derive all the properties of the numerical system with which we are familiar. Although multiplying octonions is not associative, if you need associative multiplication, you can take a special subset of octonions (we use the word "subset", but we need a special kind of subset suitable for operations in the numerical system. Such subsets are called subgroups, subfields, or "subnormal algebra with division "). So, if you select a subset of all the octonions of the form

r ₁ + r ₂ i + r ₃ j + r ₄ k + 0l + 0m + 0n + 0p

then multiplication will be associative (as in quaternions). If you go further and choose the octonions of the form

r ₁ + r ₂ i + 0j + 0k + 0l + 0m + 0n + 0p

then the multiplication will be commutative (as in complex numbers).If we continue to choose a subset of the octonions of the form

r ₁ + 0i + 0j + 0k + 0l + 0m + 0n + 0p,

then they will result in an ordered numerical system. All the necessary axioms "sit inside" octonions.

There is nothing strange about it. If we have a structure, we can concentrate on a subset of specific elements that satisfy certain requirements. Take any group. We can go through all its elements and choose X such that for all Y elements XY = YX will be true. This subset is a commutative (abelian) group. In any group there is a subset that makes up a commutative group. We simply choose those parts that satisfy the axiom, and ignore (put out of brackets) those that do not satisfy it. Our thought is that if a system has a certain structure, then particular subsets of the system will satisfy more axioms than the original system.

This is similar to what we do in physics. We do not study all phenomena. We choose those of them that satisfy the requirements of symmetry and predictability. In mathematics, we describe subsets using an axiom. In physics, we describe a selected subset of phenomena by the law of nature.

Mathematics for a subset chosen to satisfy the axiom is simpler than the mathematics of the whole set. This is because mathematicians work with axioms. They prove theorems and make up models using axioms. When there are no such axioms, mathematics becomes more difficult or even impossible.

By analogy, a subset of phenomena is easier to explain by the law of nature, written in the language of mathematics. Conversely, when we observe a larger set of phenomena, it is more difficult to find the law of nature, and this mathematics becomes more difficult or even impossible.

Working in tandem and moving forward

There is an important analogy between physics and mathematics. In both areas, if we do not study the system as a whole, but look at particular subsets, we see more structure. In physics, we take a certain phenomenon (possessing symmetry), and ignore the rest. In mathematics, we consider certain subsets of structures and ignore the rest. These two operations for the removal of brackets work together.

The task of physics is to formulate a function from a set of observable physical phenomena leading to a mathematical structure:

observable physical phenomena → mathematical structure

That is, the world we surveyed must be given a mathematical structure. As physics advances and as we try to understand more and more observable physical phenomena, we need more and more classes of mathematics. In terms of this function, if we want to increase the input of a function, we need to increase its output.

There are many examples of the expansion of physics and mathematics.

When physicists began working with quantum mechanics, they realized that ordered real numbers limit them too much. They needed a numerical system with fewer axioms. They found complex numbers.

When Albert Einstein wanted to describe GR, he understood that the mathematical structure of the Euclidean space with its plane axiom (the fifth Euclidean postulate) was too restrictive. He needed a curved, non-Euclidean space to describe the space-time in GR.

In quantum mechanics, it is known that in some systems measuring first X and then Y will lead to results different from those obtained when we first measure Y and then X. For a mathematical description of this, it is necessary to leave the cozy world of commutativity. They require a more general class of structures that do not imply commutativity.

When Boltzmann and Gibbs started talking about statistical mechanics, they realized that the laws they received were no longer deterministic. The results of the experiments were no longer divided into what happened (p (X) = 1) or did not occur (p (X) = 0). Instead, statistical theory requires probability theory. The chances of a certain experiment result are the probability, and p (X) is an element of the infinite set [0, 1], and not of the finite finite set {0, 1}.

When scientists started talking about the logic of quantum events, they realized that ordinary, distributive logic is too restrictive. They needed to form a more general logic class in which the axiom of distributivity was no longer necessarily fulfilled. Now it is called quantum logic.

Paul DiracI understood this weakening of axioms 85 years ago, when I wrote the following:

, . . , , , , , , . , . , - , . , , , , , [Dirac, PAM Quantised singularities in the electromagnetic field. Proceedings of the Royal Society 133, 60-72, (1931).].

With the development of physics and the discovery of more and more phenomena, more and more large classes of mathematical structures are required with fewer axioms with "increasing abstraction" and "generalization of axioms". No doubt, if Dirac were alive, he would have written about the arrival of octonions or even sedenions into the world of the necessary numerical systems.

To describe more phenomena, we need more and more classes of mathematical structures and less and less axioms. What is the logical conclusion of this trend? How far can it go? Physicists want to describe more and more phenomena in our universe. Suppose we want to describe all the phenomena of the universe. What kind of math do we need for this? How many axioms will need a mathematical structure that describes all phenomena? Of course, it is difficult to predict, but it is even more difficult not to speculate on this topic. One of the possible conclusions - if we look at the whole Universe at once, and we don’t put out of brackets any subsets of phenomena, then we will need mathematics without any axioms at all. That is, in general, the Universe is free from structure and axioms are not needed to describe it. Total lawlessness! Mathematics without structure is just a set. It may,finally, eliminate all metaphysics associated with the laws of nature and mathematical structures. Only the way we study the Universe gives us the illusion of having a structure.

With this view on physics, we come to an even more complex issue. These are the future projects of science. If the structure we see is illusory and comes from our way of studying certain phenomena, why do we see it? Instead of studying the laws of nature, formulated by scientists, we need to study scientists and how they choose the laws of nature, subsets of phenomena and everything related to them. What property of a person makes him such a good sieve? Instead of studying the Universe, we need to study the way we study it.

. – -. -. , « » « : , ».