Created an algorithm that generates instructions for folding origami of any shape.

In 1999, Eric Demaine (Erik Demaine), then another 18-year-old graduate student at the University of Waterloo in Canada, described an algorithm that could determine how to fold a piece of paper into any conceivable three-dimensional shape. It was a significant milestone in computational origami, but the algorithm could not create folding schemes that could actually be put into practice.

Essentially, the algorithm took as a basis a very long strip of paper and folded it into the desired shape. The structures obtained, as a rule, had many seam lines, where the layers of paper tape overlapped each other to form folds, due to which the resulting structures were not very strong.
')
In 1999, Demaine proved that any polyhedron could be folded, but the way this could be achieved was not the most effective. The proposed method works if the original sheet of paper is long and narrow. But if you need to work, for example, with a square sheet, the algorithm will still first fold the paper to a thin strip, wasting all the material for nothing.

Now Professor of Electrical Engineering and Informatics at the Massachusetts Institute of Technology, Eric Demain, and his colleague Tomohiro Tachi from Tokyo University, are ready to announce the completion of the quest that began with the work of 1999: in July 2017, they will present an algorithm for creating origami at the Symposium on Computing Geometry, which guarantees the minimum possible number of stitches. Demain and Tachi are also working on the implementation of the algorithm in the new version of Origamizer - free software for generating origami drawings. The first version was released by Taci in 2008.

The researchers' algorithm develops fold patterns to create any polyhedron, that is, a three-dimensional surface consisting of many planes. Software for creating computer graphics simulates three-dimensional objects as polyhedrons, consisting of many tiny triangles.



Strictly speaking, the guarantee that folding a sheet will include a minimum number of seams means that it retains the “borders” of the original sheet of paper. Suppose you have a round sheet of paper and you want to make a cup out of it. By leaving a smaller circle in the center of this sheet, you can connect the sides.

In this case, the border of the cup - its rim - is the same as the border of the unfolded circle - its outer edge. Demain's previous algorithm did the same thing: the bowl he offered was made up of a thin strip of paper wrapped in a reel and probably could not hold water.

Mathematical property that distinguishes both methods, scientists call "waterproof". So the new algorithm keeps the border of the original sheet of paper on the border of the surface that the user is trying to do. A closed surface, such as a sphere, has no boundaries, so origami will require a seam where these boundaries meet. We can not get a completely closed surface, but we can choose where to put the border.


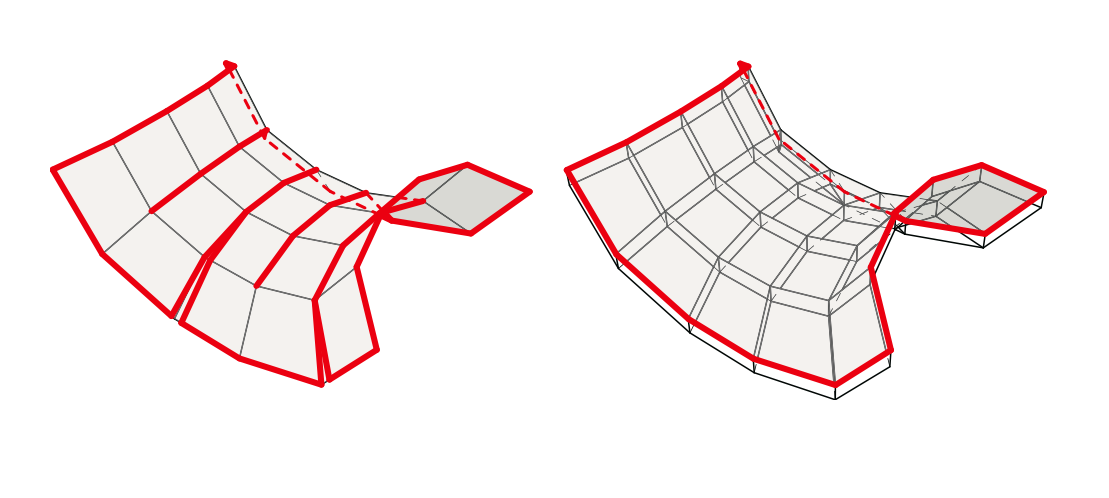
The folding of the surface according to the previous algorithm of Demain (left) and “waterproof” (right). The border of the sheet is indicated by a thick line.

At the first stage, the algorithm projects the faces of the desired shape on a flat surface. But at the time when the edges will touch, when the folding is complete, they can be quite far from each other on a flat surface. The user puts all the additional materials and combines the edges of the figure. Folding additional material can be a very complicated process. Folds connecting several sides can include dozens or even hundreds of individual folds.


Orgamizer folding rabbit scheme

The development of a method for automatically calculating origami instructions included several different ideas, but the central one was the one that could be called approximately the corresponding Voronoi diagram . To understand this concept, the authors propose to imagine a plain covered with grass. A series of lights are turned on at the same time, and all of them spread in all directions with the same speed.

The Voronoi diagram, named after the 19th century Russian scientist, Georia Voronoi, is described as the place where the lights are installed and the boundaries with which adjacent lights meet. In the algorithm of Demain and Tachi, the borders of the Voronoi diagram determine the places of the paper fold.

The work of scientists received very favorable reviews from other experts in this field. Robert Lang (Robert Lang), one of the pioneers of computational origami and a member of the American Mathematical Society , who in 2001 abandoned a successful career in the field of optical technology to become a full-fledged origami player, noted that this is a very impressive material.

Lang believes that scientists have successfully completed a long way to create a computational method for effectively bending a sheet of paper of any given shape that began 20 years ago. Along the way, some researchers managed to demonstrate several solutions to a problem that could not be called universal. We developed algorithms for folding paper of any shape, which were not very effective, as well as an algorithm for folding tree forms, but not surfaces. In his opinion, the algorithm of Demaine and Tochi is rather complicated, but this is due to a greater degree to the fact that it is also comprehensive.

doi: 10.4230 / LIPIcs.SoCG.2017.34