Ask Ethan # 43: decreasing gravitational orbits

I prefer sharp criticism from a clever man than thoughtless approval of the crowd
Johann Kepler, 1601

RealClearScience Editor asks:

Does the fact of decreasing orbits (for example, double stars) mean that there is something wrong with the laws of Newton and Kepler? Does this process explain the theory of relativity?

Let's go back to the beginning and go through the history, starting with the laws of Newton and Kepler.


')
If we take the Sun as a fixed point of reference, we will be able to track the astronomical motion of all the celestial bodies — planets, asteroids and comets — around the Sun. Using data from experiments available 400 years ago, Kepler calculated that the planets did not move in a circle with the Sun in the center, but along an elliptical path with the Sun located in one of its foci. More than 50 years after that, Newton derived the law of gravity, which produced such orbits - the law of Newton.



This law is valid not only for planets orbiting the sun, or objects falling on Earth. It is universal and acts on all objects in the Universe that have mass.

That is, if at some point you knew the position and masses of all objects of the Universe, you would be able to predictably determine the evolution of everything under the influence of gravity at any future moment in time. This is the power of Newton's laws.



But we do not need to simulate the entire Universe. To do this, firstly, you would need a computer with power from the entire Universe. Instead of counting all the movements of all subatomic particles, we just need to make a simplified model.

What if we take a very simple system - the solar system with only the planets and the sun, and Newton's laws apply to it?


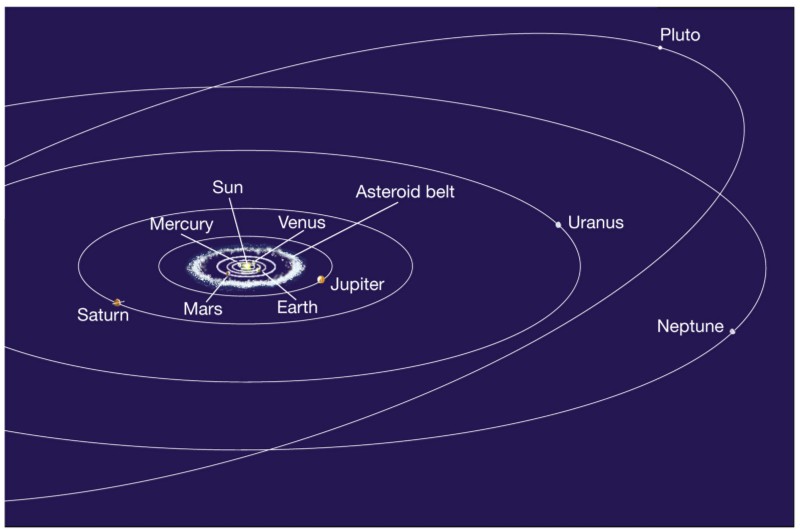
Asteroid belt and Pluto ignore

It would be possible to decide that with these nine masses separated by enormous distances, we get eight ellipses moving around the stationary Sun.

This is exactly what will happen if we accept the following:

• all planets and the sun are considered as material points
• the orbit of each planet is determined only by its interaction with the sun
• Newton's laws are absolute, there are no such things as Lorentz invariance (i.e., the laws of physics don't care about speed)

In the real world, these statements are false.



Planets and the Sun are not material points. The distances separating them are enormous compared to their size, but their sizes vary from huge (diameter of Mercury - 4879 km) to incredible (diameter of the Sun - 1391684 km). Their masses are unevenly distributed, they are denser in the core, less so on the edge. Each body in the solar system rotates with a certain angular momentum.



Other planets also have a big impact, especially over time. None of the planets move along an ideal ellipse, and the Sun does not stand still. The gravitational forces with which the bodies act on each other constantly change their orbits, and it turns out that Kepler’s calculations can be taken only as their approximation.

In fact, the planets do not move in closed ellipses, and a small amount of orbital energy is lost over time, especially if we take into account more complex phenomena, such as collisions with other particles.

This was first noted before the invention of the theory of relativity - by Oliver Haviside in 1893.



Suppose you have a central mass that creates a gravitational field. In addition, it somehow moves (the Sun is not stationary), so the gravitational field changes. And you have another massive particle moving in this field. What will happen?

It's okay if you do not know. At about the same time, scientists were dealing with a problem — what happens when a charged particle moves in an electric field. They represented the atom as a positively charged nucleus around which a negatively charged electron moves.



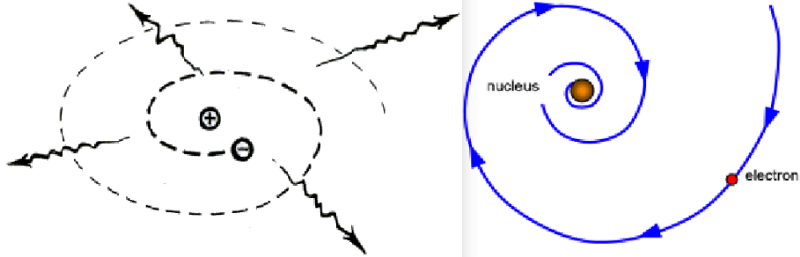
A fast moving particle emits electromagnetic radiation that carries energy. So, the orbit should decrease with time, so matter can not be stable! Rutherford discovered this problem associated with electromagnetism, and no one could solve it until they invented quantum mechanics.

In the case of gravity, we are faced with the limited predictive ability of Newton's laws. Since Newtonian gravity does not take into account the speed of motion, it does not say anything about gravitational radiation during acceleration (for example, when changing the direction of motion) when moving in a gravitational field. This is a lack of a theory in which there is no Lorentz invariance.

But just as electromagnetism exists, there must be also gravitomagnetism - since gravity is invariant according to Lorentz. You may have heard of the Gravity Probe B experiment, but in fact there is a way to measure gravitomagnetism even more accurately.



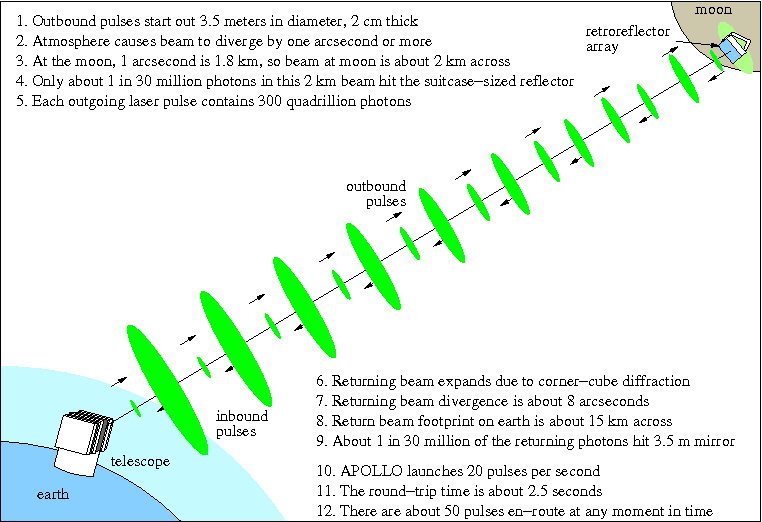
Measuring the distance to the moon with lasers, which has been available for 45 years, we not only confirmed the effect of gravitomagnetism, which is also responsible for reducing orbits, but also found that it agrees with the theory of relativity by 99.9%.

For the Earth, it will take about 10 ¹⁵⁰ years to fall on the Sun - more than the lifetime of the solar system. But for a double pulsar, everything will end in just a few hundred million years, due to the mere effect of gravitational radiation.



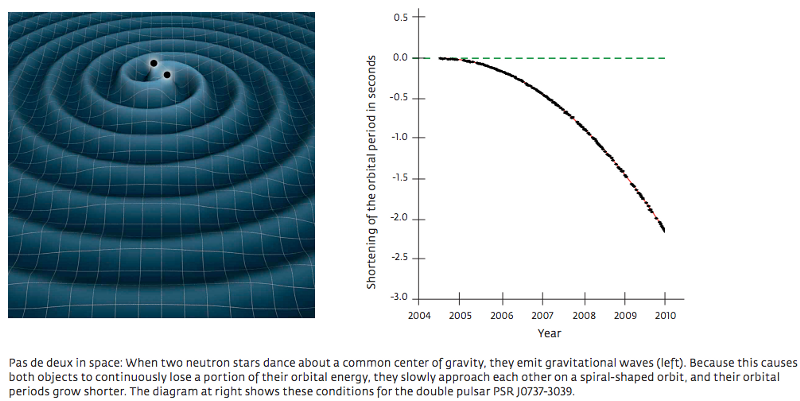
Therefore, there is a nuance in Newton's laws explaining the deviation of orbits from closed ideal ellipses, but if you want to accurately predict a decrease in orbits, you will need a Lorentz-invariant theory that preserves the laws of physics regardless of speed. And the General Theory of Relativity, after so many years, works the best!