A little-known generalization of the Pythagorean theorem
The Pythagorean theorem is perhaps the most famous of mathematical theorems. How much original evidence exists! How many uses she finds in a technique! How many benefits of civilization we owe to this great theorem! However, most recently, I discovered a completely new, previously unknown facet of this theorem, which greatly expands its scope. It is this discovery that I want to share with you, dear readers of Geektimes. Please do not judge strictly if the facts described in this article are known to you. This is a more entertaining story with a popular science element than strict math.
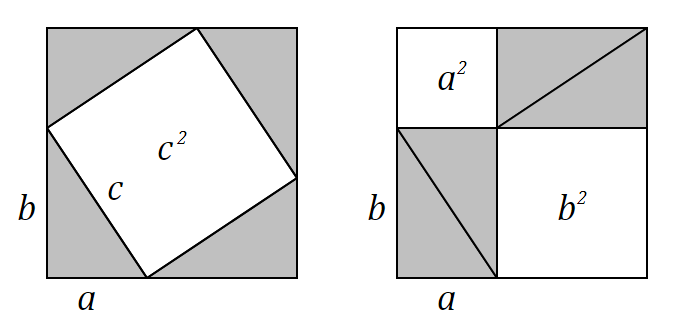
Geometric proof of the Pythagorean theorem
The history of the Pythagorean theorem goes back to centuries and millennia. In this article, we will not elaborate on historical topics. For intrigue, let us say only that, apparently, this ancient theorem was known even to ancient Egyptian priests who lived more than 2,000 years BC. For those who are curious, here is a link to the Wikipedia article .
First of all, for the sake of completeness, I would like to present here the proof of the Pythagorean theorem, which, in my opinion, is the most elegant and obvious. The figure above shows two identical squares: left and right. It can be seen from the figure that the areas of the filled-in figures are equal on the left and on the right, since in each of the large squares 4 identical rectangular triangles are painted over. This means that the unpainted (white) areas on the left and on the right are also equal. We notice that in the first case the area of the unpainted figure is , and in the second - the area of the open area is equal to
, and in the second - the area of the open area is equal to  . In this way,
. In this way,  . The theorem is proved!
. The theorem is proved!
In this article, I want to not only tell something new and cognitive about the Pythagorean theorem, but also share my story about how an interesting idea originated in my head, which I was able to formulate, prove and even suggested the possibility of generalizing to a higher dimension. But first things first.
')
Since ancient times, the science known so-called Egyptian triangles. These are right triangles in which the legs and the hypotenuse are expressed in integers. It can be said another way: Egyptian triangles are such triples of natural numbers. that form a right triangle. We all, for sure, at least once met with them at school on geometry lessons. For example, here are a few such triples:
that form a right triangle. We all, for sure, at least once met with them at school on geometry lessons. For example, here are a few such triples:
First, these are beautiful mathematical objects. And secondly, it is very convenient to solve problems with them! There are no square roots and irrational numbers in the answer.
And so, in the year 2004-2005, at the time of preparation for the Unified State Examination, when I spent days and days solving just some kind of endless break through cunning-artsy tasks from Part C, I was every now and then starting to get not three, but already four numbers had similar properties: namely, the sum of the squares of three of them gave the complete square of the fourth. This fact intrigued me so much that I still remember some of them by heart. In fact, there are infinitely many such fours and only within numbers up to 1000 there are about 84,000. But, for example, there are five such fours, one of those that the computer found brute force, while I was writing this article:
Noticing such an amazing coincidence, I began to think. The question that occupied me in connection with this mysterious circumstance, the presence of not only triples, but also fours that reveal the properties of the Egyptian triangle, was: “ What could it all mean? ” I went through the options that had only occurred to me. In the fantasy itself did not limit. Many times I sat down at the table, wrote out sets of fours known to me and looked at them thoughtfully ... for hours ... without a break ... and ... nothing happened. I had a school friend Sanya, with whom I once shared my ideas. But he was more interested in the humanities. He became a lawyer and now serves as a police major. Sanya told me something like this: “You are a strange person. You have nothing more to do. Do you ask a little homework? Stop thinking about any nonsense! " And, I must say, I thought, without ceasing, and thought for many years, from time to time returning to this riddle. While still a schoolboy, I concluded that this most likely relates to the great Fermat theorem (which I also looked at for a long time). Years went by. Nothing worked. Illumination did not come. And I realized that, probably, I would not go any further further than “something related to the Fermat theorem”. But it was not there
So, in 2014, I rode in a bus around Novosibirsk. Or maybe it was the subway. The road is not close. Do nothing. And once again I decided to think about my school riddle. And that's what I thought.
How to call these numbers? Triangles can not be called, because four numbers can not form a triangle. And here! Like a bolt from the blue
If there are such four numbers, then there must be a geometric object with the same properties reflected in these numbers!
Now it remains only to pick up a geometric object under this property, and everything will fall into place! Of course, the assumption was purely hypothetical, and had no confirmation under itself. But what if it is so!
The search of objects began. Stars, polygons, regular, irregular, right angle, and so on and so forth. Again, nothing fits. What to do? And at that moment Sherlock gets his second lead.
We must increase the dimension! A triple corresponds to a triangle on a plane, so a quadruple corresponds to something three dimensional!
Oh no! Again bust options! And in three dimensions, there are much, much more various geometric bodies. Try to sort through them all! But it is not all that bad. There is also a right angle and other clues! What we have? Egyptian fours numbers (let them be Egyptian, you must call them somehow), a right angle (or corners) and a certain three-dimensional object. Deduction worked! And ... I suppose that the quick-witted readers have already understood that we are talking about pyramids, with which at one of the peaks all three corners are straight. You can even call them rectangular pyramids by analogy with a right triangle.
So, we have everything we need. Rectangular (!) Pyramids, lateral faces-legs and a cutting- edge hypotenuse . It's time to draw another picture.
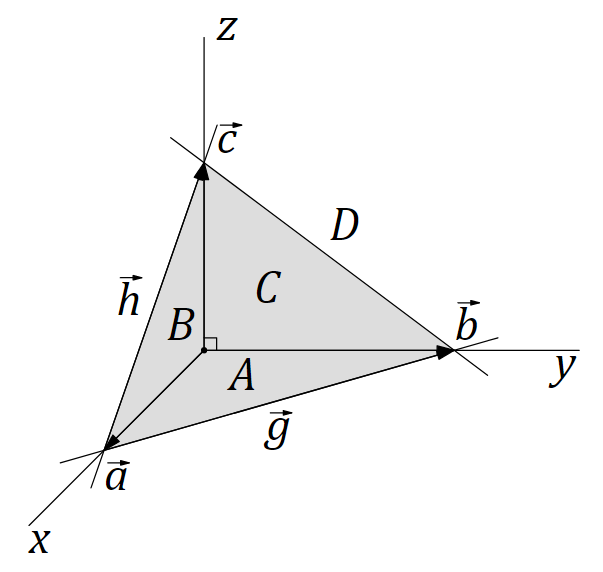
Pythagorean theorem for a rectangular pyramid
The picture shows a pyramid with a vertex at the beginning of the rectangular coordinates (the pyramid lies, as it were, on its side). The pyramid is formed by three mutually perpendicular vectors, laid out from the origin along the coordinate axes. That is, each side face of the pyramid is a right triangle with a right angle at the origin. The ends of the vectors define the cutting plane and form the base of the pyramid.
Of course, if the ordinary Pythagorean theorem is formulated for the lengths of the sides of the triangles, then our theorem is formulated for the areas of the sides of the pyramid. It is very easy to prove this theorem in three dimensions if you know a little vector algebra.
My delight knew no bounds! I literally jumped from happiness. Of course, this is not God knows what a complicated theorem, and the proof is very simple, but you see. And to me - no one! I was sincerely convinced of this for about a year. Attempts to find at least some evidence that this is already known and proven failed one by one, and I thought that I had made the discovery. This is an unavoidable feeling! I wanted to share this theorem with the world. I talked about it to friends who are familiar to mathematicians, just familiar with technical / mathematical education and without. No one shared my enthusiasm and enthusiasm. Everyone was just indifferent. As if I did not invent and proved the theorem, I just went to the store for bread. So what's wrong with that? This is really ... As they say, “How boring we live! The spirit of adventurism has disappeared in us, we stopped climbing windows to our beloved women, we stopped doing big good nonsense. ”(From the film“ The Irony of Fate ”).
Of course, like a person who is professionally engaged in research, something like this has happened in my life more than once. But this moment was the brightest and most memorable. I experienced a full range of feelings, emotions, experiences of the discoverer. From the origin of thought, the crystallization of the idea, the finding of evidence, to complete misunderstanding and even rejection, which my ideas met with my friends, acquaintances and, as it seemed to me then, to the whole world. It was unique! I felt as if I were in the shoes of Galileo, Copernicus, Newton, Schrödinger, Bohr, Einstein and many, many other discoverers.
In life, everything turned out to be much simpler and more prosaic. I was late ... But by how much! Only 18 years old! Under terrible lengthy torture and not the first time, Google confessed to me that this theorem was published in 1996!
Here is a link to the article:
Amir-Moéz, Ali R., Robert E. Byerly, and Robert R. Byerly. “Pythagorean theorem in unitary spaces.” Publikacije Elektrotehničkog fakulteta. Serija Matematika (1996): 85-89.
The article was published by Texas Tech. The authors, professional mathematicians, introduced the terminology (which, by the way, largely coincided with mine) and also proved a generalized theorem that is valid for a space of any dimension greater than one. What happens in dimensions higher than 3? Everything is very simple: instead of faces and areas there will be hypersurfaces and multidimensional volumes. And the statement, of course, will remain the same: the sum of the squares of the volumes of the lateral faces is equal to the square of the base volume — simply the number of faces will be larger, and the volume of each of them will be equal to half the product of the generators. Imagine it is almost impossible! You can only, as the philosophers say, to think!
What is surprising, having learned that such a theorem is already known, I was not upset at all. Somewhere in the depths of my soul I suspected that it was quite possible that I was not the first, and I understood that one must always be ready for this. But that emotional experience that I received, sparked the spark of an explorer in me, which, I am sure, will never fade away now!
Erudite reader in the comments sent a link
Theorem de gua
So I was late not for 18 years, but at least for a couple of centuries!
Readers pointed out in the comments a few useful links. These and some other links:

Geometric proof of the Pythagorean theorem
Around and around
The history of the Pythagorean theorem goes back to centuries and millennia. In this article, we will not elaborate on historical topics. For intrigue, let us say only that, apparently, this ancient theorem was known even to ancient Egyptian priests who lived more than 2,000 years BC. For those who are curious, here is a link to the Wikipedia article .
First of all, for the sake of completeness, I would like to present here the proof of the Pythagorean theorem, which, in my opinion, is the most elegant and obvious. The figure above shows two identical squares: left and right. It can be seen from the figure that the areas of the filled-in figures are equal on the left and on the right, since in each of the large squares 4 identical rectangular triangles are painted over. This means that the unpainted (white) areas on the left and on the right are also equal. We notice that in the first case the area of the unpainted figure is
The origin of the idea
In this article, I want to not only tell something new and cognitive about the Pythagorean theorem, but also share my story about how an interesting idea originated in my head, which I was able to formulate, prove and even suggested the possibility of generalizing to a higher dimension. But first things first.
')
Egyptian Triangles
Since ancient times, the science known so-called Egyptian triangles. These are right triangles in which the legs and the hypotenuse are expressed in integers. It can be said another way: Egyptian triangles are such triples of natural numbers.
First, these are beautiful mathematical objects. And secondly, it is very convenient to solve problems with them! There are no square roots and irrational numbers in the answer.
Mysterious Fours
And so, in the year 2004-2005, at the time of preparation for the Unified State Examination, when I spent days and days solving just some kind of endless break through cunning-artsy tasks from Part C, I was every now and then starting to get not three, but already four numbers had similar properties: namely, the sum of the squares of three of them gave the complete square of the fourth. This fact intrigued me so much that I still remember some of them by heart. In fact, there are infinitely many such fours and only within numbers up to 1000 there are about 84,000. But, for example, there are five such fours, one of those that the computer found brute force, while I was writing this article:
Noticing such an amazing coincidence, I began to think. The question that occupied me in connection with this mysterious circumstance, the presence of not only triples, but also fours that reveal the properties of the Egyptian triangle, was: “ What could it all mean? ” I went through the options that had only occurred to me. In the fantasy itself did not limit. Many times I sat down at the table, wrote out sets of fours known to me and looked at them thoughtfully ... for hours ... without a break ... and ... nothing happened. I had a school friend Sanya, with whom I once shared my ideas. But he was more interested in the humanities. He became a lawyer and now serves as a police major. Sanya told me something like this: “You are a strange person. You have nothing more to do. Do you ask a little homework? Stop thinking about any nonsense! " And, I must say, I thought, without ceasing, and thought for many years, from time to time returning to this riddle. While still a schoolboy, I concluded that this most likely relates to the great Fermat theorem (which I also looked at for a long time). Years went by. Nothing worked. Illumination did not come. And I realized that, probably, I would not go any further further than “something related to the Fermat theorem”. But it was not there
Sherlock found a clue
So, in 2014, I rode in a bus around Novosibirsk. Or maybe it was the subway. The road is not close. Do nothing. And once again I decided to think about my school riddle. And that's what I thought.
How to call these numbers? Triangles can not be called, because four numbers can not form a triangle. And here! Like a bolt from the blue
If there are such four numbers, then there must be a geometric object with the same properties reflected in these numbers!
Now it remains only to pick up a geometric object under this property, and everything will fall into place! Of course, the assumption was purely hypothetical, and had no confirmation under itself. But what if it is so!
The search of objects began. Stars, polygons, regular, irregular, right angle, and so on and so forth. Again, nothing fits. What to do? And at that moment Sherlock gets his second lead.
We must increase the dimension! A triple corresponds to a triangle on a plane, so a quadruple corresponds to something three dimensional!
Oh no! Again bust options! And in three dimensions, there are much, much more various geometric bodies. Try to sort through them all! But it is not all that bad. There is also a right angle and other clues! What we have? Egyptian fours numbers (let them be Egyptian, you must call them somehow), a right angle (or corners) and a certain three-dimensional object. Deduction worked! And ... I suppose that the quick-witted readers have already understood that we are talking about pyramids, with which at one of the peaks all three corners are straight. You can even call them rectangular pyramids by analogy with a right triangle.
New theorem
So, we have everything we need. Rectangular (!) Pyramids, lateral faces-legs and a cutting- edge hypotenuse . It's time to draw another picture.

Pythagorean theorem for a rectangular pyramid
The picture shows a pyramid with a vertex at the beginning of the rectangular coordinates (the pyramid lies, as it were, on its side). The pyramid is formed by three mutually perpendicular vectors, laid out from the origin along the coordinate axes. That is, each side face of the pyramid is a right triangle with a right angle at the origin. The ends of the vectors define the cutting plane and form the base of the pyramid.
Theorem
Let there be a rectangular pyramid formed by three mutually perpendicular vectorswhose facets are square -
, and the area of the face-hypotenuse -
. Then
Alternative wording: A four-sided pyramid, in which all flat angles are right at one of the vertices, the sum of squares of the side faces is equal to the square of the base area.
Of course, if the ordinary Pythagorean theorem is formulated for the lengths of the sides of the triangles, then our theorem is formulated for the areas of the sides of the pyramid. It is very easy to prove this theorem in three dimensions if you know a little vector algebra.
Evidence
Express squarethrough lengths of vectors
.
Where.
Squarewe represent as half the area of the parallelogram built on the vectors
and
As is known, the vector product of two vectors is a vector whose length is numerically equal to the area of the parallelogram built on these vectors.
therefore
In this way,
Q.E.D!
EUREKA!
My delight knew no bounds! I literally jumped from happiness. Of course, this is not God knows what a complicated theorem, and the proof is very simple, but you see. And to me - no one! I was sincerely convinced of this for about a year. Attempts to find at least some evidence that this is already known and proven failed one by one, and I thought that I had made the discovery. This is an unavoidable feeling! I wanted to share this theorem with the world. I talked about it to friends who are familiar to mathematicians, just familiar with technical / mathematical education and without. No one shared my enthusiasm and enthusiasm. Everyone was just indifferent. As if I did not invent and proved the theorem, I just went to the store for bread. So what's wrong with that? This is really ... As they say, “How boring we live! The spirit of adventurism has disappeared in us, we stopped climbing windows to our beloved women, we stopped doing big good nonsense. ”(From the film“ The Irony of Fate ”).
Of course, like a person who is professionally engaged in research, something like this has happened in my life more than once. But this moment was the brightest and most memorable. I experienced a full range of feelings, emotions, experiences of the discoverer. From the origin of thought, the crystallization of the idea, the finding of evidence, to complete misunderstanding and even rejection, which my ideas met with my friends, acquaintances and, as it seemed to me then, to the whole world. It was unique! I felt as if I were in the shoes of Galileo, Copernicus, Newton, Schrödinger, Bohr, Einstein and many, many other discoverers.
Afterword
In life, everything turned out to be much simpler and more prosaic. I was late ... But by how much! Only 18 years old! Under terrible lengthy torture and not the first time, Google confessed to me that this theorem was published in 1996!
Here is a link to the article:
Amir-Moéz, Ali R., Robert E. Byerly, and Robert R. Byerly. “Pythagorean theorem in unitary spaces.” Publikacije Elektrotehničkog fakulteta. Serija Matematika (1996): 85-89.
The article was published by Texas Tech. The authors, professional mathematicians, introduced the terminology (which, by the way, largely coincided with mine) and also proved a generalized theorem that is valid for a space of any dimension greater than one. What happens in dimensions higher than 3? Everything is very simple: instead of faces and areas there will be hypersurfaces and multidimensional volumes. And the statement, of course, will remain the same: the sum of the squares of the volumes of the lateral faces is equal to the square of the base volume — simply the number of faces will be larger, and the volume of each of them will be equal to half the product of the generators. Imagine it is almost impossible! You can only, as the philosophers say, to think!
What is surprising, having learned that such a theorem is already known, I was not upset at all. Somewhere in the depths of my soul I suspected that it was quite possible that I was not the first, and I understood that one must always be ready for this. But that emotional experience that I received, sparked the spark of an explorer in me, which, I am sure, will never fade away now!
PS
Erudite reader in the comments sent a link
Theorem de gua
Excerpt from Wikipedia
In 1783, the theorem was presented to the Paris Academy of Sciences by the French mathematician J.-P. de Gua, however, earlier she was known to René Descartes [3] and before him to Johann Fulhgäber (Eng.), who probably first opened it in 1622 [4]. In a more general form, the theorem was formulated by Charles Tinzo (Fr.) in a report by the Paris Academy of Sciences in 1774 [4]
So I was late not for 18 years, but at least for a couple of centuries!
Sources
Readers pointed out in the comments a few useful links. These and some other links:
Source: https://habr.com/ru/post/371169/
All Articles