Naturalness and Standard Model

What is "naturalness?"

What do particle physics and string theory specialists mean when they say that a certain set of particles and interactions is “natural”? They do not mean that he is "part of nature." In the universe, everything is by definition a part of nature.

The word "natural" has many meanings. Scientists in our context do not use the meaning “associated with nature”, but the meaning “typical” or “generalized”, “expected”, “ordinary”. For example: "naturally, the child, hitting his head, screamed," or "naturally, it is worth living more close to the center", or "I have not worn these glasses for many months, and they, of course, have become dusty." And unnatural - this is when the child does not scream, when in the center of the city is cheap, and when the glasses are clean. Usually, when something unnatural happens, there is a reason for that.

In most contexts of particle physics and related topics, surprises are extremely rare. This means that when you look at the physical system, you will see that it behaves the way you, having gained some scientific experience, can expect from it. And if she does not behave this way, then, as experience shows, there is a reason for that. And if this reason is not obvious, then the unnatural behavior of the system may speak about some kind of extreme effect that you still do not know.

For our purposes, the concept of naturalness is important because in nature there are two big surprises that we, particle physics specialists, and our friends have to face. The first is that the cosmological constant (which is often called dark energy) is surprisingly small compared to what one would expect in a natural way. The second is that the hierarchy between the force of gravity and the force of other interactions is surprisingly large compared to what one would expect.
')
The second surprise can be reformulated as follows: The Standard Model (together with Einstein's theory of gravity) —a set of equations we use to predict the behavior of all known elementary particles and forces — surprisingly, extremely, incredibly unnatural theory. In physics, there is only one more aspect — perhaps the only aspect in all science — even less natural than the Standard Model, and this is the cosmological constant.

The concepts of natural and unnatural

I believe that one story will best describe the concept of naturalness.

A couple of my friends from college, let's call them Anya and Steve, got married, and now they have two teenage children. When these children were younger - they were 4 and 7 years old - they behaved like savages. They played hard, resented each other, threw things at them, and constantly had to look after them.

Once Anya bought very beautiful flowers and put them in her favorite glass vase. But before she could put the vase on the kitchen table, the doorbell rang. She ran with the vase to the door, and on the way, without thinking, put the vase on a small unstable table that stood next to the wall of the children's playroom.

Half an hour later, Steve returned home with the children, and sent them to the game room so that they would stay there while she and Anya came to their senses after work and prepared dinner. They heard the usual sounds: hitting, falling, the sound of bouncing balls and falling toys, shouts of “dishonest” and “stop”, a shout that ended almost immediately after it began.

After 45 minutes, Anya noticed that there was no vase with flowers on the kitchen table. Looking for her in the kitchen and in the dining room, she suddenly remembered that she had set it and forgot it in the most dangerous place in the house.

She ran into the game room, hoping she was not late. And what do you think she found there when she opened the door?

Guess it. You have three options (Fig. 1). Choose the most likely:

1. The vase stood in the same place where she left it, neatly placed in the center of the table.
2. The vase was broken, and the crushed flowers lay on the floor.
3. A vase hung from the table right on the edge, a millimeter from the crash.


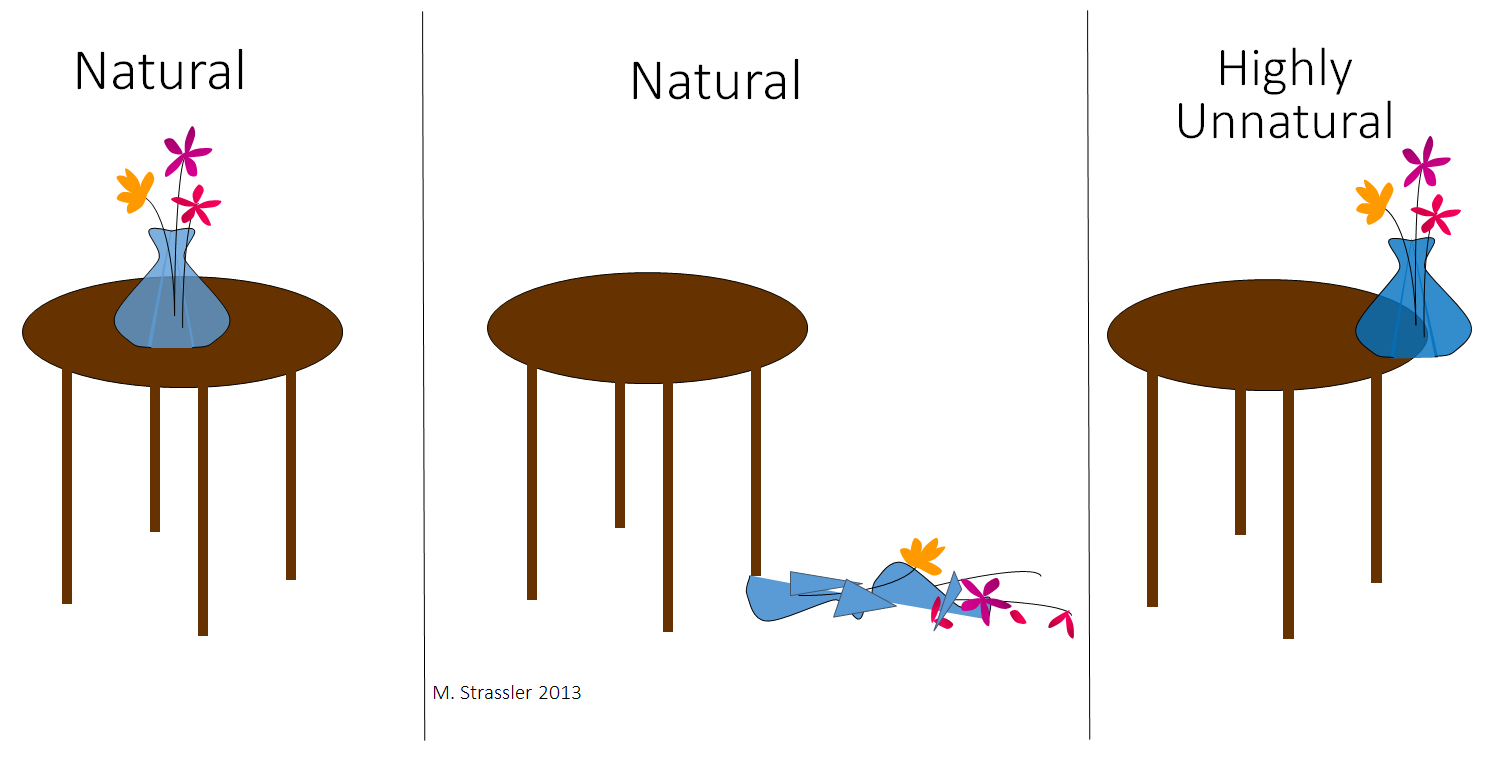
Fig. one

The correct answer is # 3. It hung from the edge.

I suspect you don't believe me. At least, even if you believe, you think that there must be some complicated explanation for what happened, and I will give it to you. It is unbelievable that two small children go crazy in a room and somehow accidentally bring the vase to such an unreliable location. Since the fact that the vase was there - not standing firmly on the table, not falling on the floor, but somewhere in the middle - this is ... unnatural!

There must be an explanation.

Maybe there was glue on the edge of the table, and the vase stuck to it before it fell? Maybe one of the children was hiding at the table and holding a vase to play mom? Maybe her husband tied a thread around the vase and attached it to the table, or to the ceiling so that the vase would not fall? Maybe the vase and the table are magnetized?

Something so unnatural could not happen by itself. Especially in a room in which two children are raging and being thrown by things.

The unnatural nature of the Standard Model

We now turn to the Standard Model, combined with Einstein's theory of gravity.


Fig. 2

Imagine resembling our Universe, described by a complete set of equations — in the language of theoretical physics this is called theory — like the Standard Model (plus gravity). For simplicity, let us assume that in this Universe there are all the same elementary particles and interactions as in ours. The difference is that the strength of the interactions, and the force with which the Higgs field interacts with other known particles and with itself (which determines the mass of known particles), is slightly different from ours - say, 1%, 5% or even by 50%. In general, let's imagine ALL such universes. All universes are described by equations of the Standard Model type, in which the interaction force of all fields and particles with each other varies up to 50%. What will the worlds described by these slightly different equations look like (worlds are shown in Figure 2 as a handful?)

Among imaginary worlds, we find three main classes with the following properties.

1. The average value of the Higgs field is zero; that is, the Higgs field is disabled. In such worlds, the mass of the Higgs particle will be ten thousand trillion (10,000,000,000,000) times greater than in ours. All other known elementary particles will be massless (with the exception of some individual features). In particular, the electron will not have mass, and in this world there will be no atoms.

2. The Higgs field is included in full. Its average value, and the mass of the Higgs particle, and the mass of all known particles, will be ten thousand trillion (10,000,000,000,000) times more than in our universe. In such a world there will be no atoms or habitual large objects. For example, neither a star nor a planet will be able to form there - they will surely collapse into a black hole.

3. The Higgs field is turned on by a small amount. Its average value approximately corresponds to ours - perhaps several times more or less, but comparable. Masses of known particles, although they will differ from those in our world, but not much. And all the particles that have mass in our world will have mass. Atoms, planets, and other structures can even appear in some of these worlds. In others there may be exotic and unusual things to us. But at least some basic properties of such worlds will be familiar to us.

What is the proportion of worlds in class number 3? Among all the theories of the Standard Model type that we are considering, what proportion will be at least a bit like ours?

To ridiculous, to the absurd a small fraction (Fig. 3). If you randomly select the Universe from our set of worlds similar to the Standard Model, then the chance that it will remind us a little bit will be incredibly less than what you blithely left a vase on the table and it turned out to be on the verge of disaster purely by accident.


Fig. 3

In other words, if the Standard Model (plus gravity) describes everything that exists in our world, then among all possible worlds we live in an extremely unusual - as unnatural as a vase spaced at a width of one atom from falling from the table. Classes 1 and 2 universes are natural, typical, generalized. Most of the theories of the Standard Model type will produce a universe of these classes. Class 3, which includes our Universe, includes possible, but unnatural and atypical worlds. What happened to us to live in such an unusual universe — especially since we live, quite naturally, on an ordinary planet orbiting a regular star in an ordinary galaxy — unexpectedly, shockingly, and strangely. And deserves, like the oddly arranged vase, an explanation. Definitely, one has to suspect the existence of a hidden mechanism, something related to the universe, that while we do not know what allows our universe to live naturally on the edge.

And the analogy of playing children, putting a vase in danger and making its balanced arrangement unlikely? This is quantum mechanics itself - the basic principles of the work of the world. Quantum effects cannot coexist peacefully with a random and unstable balance.

A little later, I will move on to the discussion of quantum effects and how they make the Standard Model unnatural. But first, although I hope you like my story, I want to point out that there is one important difference between the vase on the table and the universe. If someone hits a table with a vase, it is likely to fall, or, if we are lucky, it slips to the center of the table. In other worlds, she can easily move from her shaky position. For our universe, on the contrary, there is no danger of smoothly changing its properties and becoming a universe of classes 1 or 2. Although it is possible that someday it will suddenly change and become completely different due to a process called tunneling or vacuum decay, this event is unprecedentedly far from us. Don't worry about it.

The real problem of the universe is in the past: how, among a huge number of possible universes, we found ourselves in such an unnatural? Is there something in our universe that we don’t know yet that makes it not as unnatural as it seems? Or is it somehow connected with the fact that many (most) natural universes are not adapted for life? Or perhaps people are not smart enough yet, and there is another scientific explanation for this? Whatever the reason, it is either related to a fact outside of time, or to something that happened a long time ago; the universe (more precisely, at least the area that we can observe with our eyes and telescopes) has always remained unnatural (if the Standard Model fully describes it) billions of years, and will not change in the near future.

In any case, we proceed further and examine quantum physics, which makes the universe described by the Standard Model (and gravity) so incredibly unusual.

Quantum physics and (un) naturalness

Before further reading, you must first read about quantum fluctuations and their energy . In that article you will find another problem of naturalness: the problem of the cosmological constant.

Back to the Higgs (and other similar particles)

Quantum fluctuations of fields and their contribution to the energy density of empty space (the so-called vacuum energy) play a large role in our history. But our goal obliges us to set aside the problem of the cosmological constant and concentrate on the Higgs particle and on why the Standard Model is unnatural. We will do this not because the problem of the cosmological constant is not very important, and not because we are sure that these two problems are not interconnected. But since the cosmological constant is directly related to gravity, and the problem of the Higgs particle and the naturalness of the Standard Model are not directly connected with gravity, it is quite possible that they are solved in different ways. And each of the two problems in itself is unrealistically complex; if we have to solve them at the same time, then everything will be even worse. So let's send the cosmological constant to the corner for now, so that it lies there. But we will remember that there is an elephant in the room, which we cannot ignore forever.

Now to the Higgs field. We need to answer three very important questions related to the Higgs field and its particle. I will formulate these questions on the assumption that the Standard Model is true, or almost true. But if this is not the case, do not worry: the ideas being studied will remain essentially the same, even if you need to rephrase them a bit.

1. Higgs field included. Its average value is always and everywhere, at least from the earliest stages of the life of the Universe, non-zero. Why?
2. Its average value is 246 GeV. What sets it up?
3. The mass of the Higgs particle is approximately 125 GeV / s ² . What sets it up?

I will explain to you how and why these questions are related to the problem of the dependence of the energy of empty space (part of which stems from quantum field fluctuations) on the mean value of the Higgs field.

Higgs field size and empty space energy

How to determine the average value of any field (not just the Higgs field) in the Universe? Answer: the average value of the field should have the following property: if you change its value a little, increasing or decreasing, then the energy of empty space should increase. In short, the field value should be such that the energy of empty space in this case will be at a minimum — not necessarily at the very minimum, but one of the local ones (if there are more than one minimum, then the choice of a particular one may depend on the history of the Universe, or more complex things that I will not touch on so far).

A couple of examples of how the energy of empty space in our Universe, or in some imaginary universe, may depend on the Higgs field, or on some other similar field, is shown in fig. 4. In each of the two cases, I drew two minima where the Higgs field can be located - but this is a random choice. In other cases, there may be more than two minima, or only one. From the fact that in our world the Higgs field is included, it follows that there is a minimum in the vacuum energy of the universe for which the value of the Higgs field is 246 GeV. And although this is not obvious from my previous story, we are confident, based on what we know about nature and equations, that there is no minimum in which the Higgs field is zero and therefore the Higgs field is not turned off in our Universe. So in our Universe, the dependence of the vacuum energy on the Higgs field seems to look more like the left part of the picture than the right, but, as we will see, it may be different from any of them. If the Standard Model describes physics at much higher energies and at much shorter distances than those we study at the Large Hadron Collider, then the shape of the corresponding curve will be much more complicated - as we will see later.


Fig. 4: horizontal - the average value of the Higgs field, vertical - the energy density. The mass of the Higgs particle is given by the curvatures of the graph, which form minima.

Higgs particle mass and empty space energy

What about the Higgs particle mass? It is determined (Fig. 4) by how quickly the energy of empty space changes when the value of the Higgs field deviates from the preferred one. Why?

The Higgs particle is a small perturbation of the Higgs field — that is, as the Higgs particle passes, the Higgs field has to change a little, it becomes larger or smaller. Since we know that the average value of the Higgs field is at the minimum of the energy of empty space, any small change in this value slightly increases this energy. This additional energy (in fact, its half) and gives the energy of the mass of the Higgs particle (through E = mc ² ). If the shape of the curve around the minimum is very flat, then the production of the Higgs particle requires little energy, since the additional energy in the perturbation of the Higgs field will be small. But if near the minimum the curve is strongly bent, then the Higgs particle has a large mass.

Thus, the plane or sharpness of the curve on the graph where the value of the Higgs field is located — the curvature at the minimum — determines the mass of the Higgs particle.

Why is it difficult to make the Higgs particle mass small?

The measured mass of the Higgs particle is approximately 125-126 GeV / s ² , which is about 134 times the mass of a proton. Why can't we just substitute this mass into our equations and end up with a question, where did it come from?

The problem is that the value of the Higgs field, and the mass of the Higgs particle are not substituted into the equations we use directly; they are derived from the equations we use with the help of complex calculations. And here we are faced with certain difficulties.

We get these two numbers — the average value and the mass of the field and the particle — by studying how the energy of empty space depends on the Higgs field. And this energy, as in any field theory, such as the Standard Model, is the sum of many things:

• fluctuation energies of the Higgs field itself,
• fluctuation energy of the upper quark field,
• fluctuation energy of the field W,
• fluctuation energy of the field Z,
• ,
• ,
• …

, . ( ) . 5. , , , , v _max .

, . , ; , , v _max – . , , , ( , , – ), . This is not true. , .


Fig. 5: , ,

v _max ? , , , . v _max , ( , v _max / ² ), . , v _max — , , , .

v _max . . , , v _max 500 . , , , , v _max 10 000 000 000 000 000 . , . v _max , , ! , . – .

, , v _max - 500 1 000 000 000 000 000 000 . In fig. 5 , 500 . . 6, 500 .

, . 5, ( , , , ) v _max , v _max . ( – E _max , v _max , ). v _max , – , , , v _max , – v _max ⁴ / (hc) ³ .

But that is not all. , . 5, , , , . , . , , , , . , :

• ,
• , ,
• , , , ;
• , , , D- , - ,
• - …

, , . . 100% . , , ( ), , . , , , . , – , , , , .

, , , , , . , - , , - W? .

, . , , , – , . . ; , , 246 . , , , ( ) . , , , . How did this happen?

? ? v _max . v _max 500 , – . . 6. v _max , , . 5. v _max , .


Fig. 6

? (v _max /500 ) ² . v _max 500 , ; v _max = 5000 , 100. 500 000 , .

v _max – – 1 000 000 000 000 000 000 000 000 000 000.

. , W - – , – , 1 2, - , , (. . 3). , – , . .

: , , v _max , 500 , , . 5. . v _max , . , , . 5, , , v _max , , , – :

• , v _max ( 2 – . . 3),
• ( 1),
• - - v _max ( 3).

, , ( , v _max / ² , 1 2), ( , , v _max / ² , 3). . 7, , , .


Fig. 7: – , . – .

. , . 5 , , . , – , , , , , .

,

, , – " ", - . , , – – , , , - , .

. ( ) .

, – , , , v _max , , , . — , , .


Fig. eight

– , 1980-. , . (. 8) v _max , , , . , v _max ( . 5, ), , , v _max . , . – ? v _max / ² ? v _max ? ! , , – .

, , , . , , , (, , ).

( , , ). . v _max , , , , 500 , .

: , , , .

. [ , , – … / . trans. ]