Poisson equation and Boltzmann distribution (part 1)
Poisson equation
We found out that the plasma is quasineutral in an equilibrium state and that under the action of an electric field from moving charges, the charged particles are displaced by the Debye length and the field within this length is damped. In electrostatics, the interaction of charged particles is described by the Coulomb equation:
')
F=k fracq1q2r212
Where q1,q2 - the magnitude of the interacting point charges, r212 - The square of the distance between the charges. The coefficient k is constant. If we use the system in electrostatic units of the GHS, referred to as CGSEq, then k = 1. If the SI system is used, then k= frac14 pi epsilon epsilon0 where epsilon - the dielectric constant of the medium in which the charges are located, epsilon0 - electric constant equal to 8.86 10−12m−3kg−1c4F2 .
In physics, they do not directly use force, but introduce the concept of an electrostatic field of distributed charges and measure a field by the magnitude of the electric field intensity . To do this, mentally place a single trial charge at each point of the field and measure the strength with which the charge field acts on the trial charge:
E= fracFq0
Hence, if we substitute the Coulomb force into this equation, we get:
E= sumNj=1 fracqjr20j
But physicists are not limited to this either, in order to describe a fully electric field. Consider a unit charge placed in an electrostatic field. The field does the work of moving this charge at an elementary distance ds from point P1 to point P2:
phi21=− intp2p1Eds(∗)
Magnitude phi21 called potential difference or voltage. Voltage is measured in Volts. The minus sign tells us that the field itself does the work to transfer a unit of positive charge. The forces moving the charges are conservative, since the work along a closed path is always zero, no matter which way the charge moves.
Hence follows the deep meaning of the potential difference. If we fix the point P1 and move the charge to the variable point P2, then the work depends only on the position of the second point P2. Thus, we can introduce the concept of potential. A potential is a force function, showing what kind of work the field needs to perform in order to move the charge from infinity to a given point P2, where conditionally the potential at infinity is zero.
To understand the Poisson equation, it is necessary to understand the "special" vector mathematics. I will briefly describe such concepts as field gradient and divergence (it is understood that the reader is familiar with mathematical analysis)
Let f (x, y, z) be some continuous differentiable function of coordinates. Knowing its partial derivatives partialf/ partialx, partialf/ partialy, partialf/ partialz at each point in space, you can construct a vector whose components x, y, z are equal to the corresponding partial derivatives:
nablaf= vecx frac partialf partialx+ vecy frac partialf partialy+ vecz frac partialf partialz
Where vecx, vecy, vecz - unit vectors of the corresponding x, y, z axes. Icon nabla reads "nabla" and is a differential operator
nabla= frac partial partialx+ frac partial partialy+ frac partial partialz
This operator introduced Hamilton to mathematics. With Nabla you can perform ordinary mathematical operations, such as ordinary work, scalar product, vector product, and so on.
Now back to the electrostatic field E. On the one hand, the change in potential during the transition from one point to another has the following form:
d phi= frac partial phi partialxdx+ frac partial phi partialydy+ frac partial phi partialzdz
On the other hand, according to the formula (*)
d phi=−Eds
Applying the gradient concept just introduced, this formula translates to:
E=− nabla phi(∗∗)
Now let's deal with such a concept as the divergence of the field. Consider a finite closed volume V of arbitrary shape (see figure below). Denote the area of this surface S. The total flux of the vector F coming out of this volume is, by definition, equal to
F= intSFda
where da is an infinitely small vector whose value is equal to the area of the small element of the surface S, and the direction coincides with the outward normal to this element.
Take this flow of vector F divided by the volume Vi and find the limit at Vi tending to zero, i.e. We will push the volume to an infinitely small point.
divF= limVi to0 frac1Vi intSFda
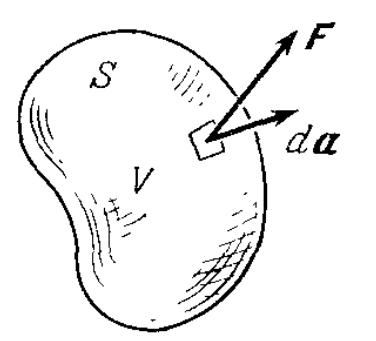
We come to the concept of divergence. The divergence is denoted by the symbol div and is the ratio of the flux of the vector F to the volume V, with V tending to zero.
Before showing how the Poisson equation is obtained, it is important to know the Gauss law and the Gauss theorem. Imagine a sphere, inside which is the charge q. The charge creates around itself an electric field of intensity E. Take the flux of the vector E
F=(E,S)
where S is the area of our sphere equal 4 pir2 . Consequently
F= fracqr24 pir2=4 piq
This is the Gauss law, which states that the flow of the electric field E through any closed surface is equal to the product 4 pi on the full charge covered by the surface:
intSEda=4 pi sumiqi=4 pi int rhodv
Where rho - density of the space charge, i.e. the amount of electric charge per unit volume, and dv - the elementary volume allocated inside our closed volume.
The Gauss theorem (the full name of the Gauss-Ostrogradsky theorem) is a purely mathematical divergence theorem. Rewrite the total flow of the vector F as follows:
intSFda= sumNi=1 intSiFdai= sumNi=1Vi frac intSiFdaiVi
In the limit, when N → ∞, Vi → 0, the value in brackets becomes a divergence and the sum goes to the volume integral:
intSFda= intVdivFdv
This is the Gauss theorem, and is truly the most important formula of the field theory. Apply this theorem to an electrostatic field. On the one hand, according to the law of Gauss
intSEda=4 pi int rhodv
On the other hand, according to the Gauss theorem (just do not confuse the theorem with the Gauss law):
intSEda= intVdivEdv
Combining the last two equations, we get:
divE=4 pi rho
Recall the formula (**) and substitute here, instead of E, the potential of the field
div nabla phi=−4 pi rho
Gradient divergence is a new operator, which in mathematics is called the Laplace operator, or the abbreviated Laplacian. Laplacian is denoted by the icon nabla as follows nabla2 and equals
nabla2= frac partial2 partialx2+ frac partial2 partialy2+ frac partial2 partialz2
Rewrite the previous formula in the form of a Laplacian:
nabla2 phi=−4 pi rho
Finally we got the Poisson equation. In the first article, this equation was slightly different form, taking into account the dielectric constant of the medium. Remember the Coulomb force in the SI system, there is a constant k= frac14 pi epsilon epsilon0 . Accordingly, the Gauss law will not 4 pi and coefficient frac1 epsilon epsilon0 . Thus, we obtain the Poisson equation in the form presented in the previous article.
nabla2 phi=− frac1 epsilon epsilon0 rho=− frac1 epsilon epsilon0 sumiqini
Thus, in essence, the Poisson equation is the Coulomb law (more precisely, the Gauss law) rewritten in a different form, in the notation of vector differential analysis.
In the next article we will analyze the important distribution from mathematical statistics - the Boltzmann distribution.
Source: https://habr.com/ru/post/370799/
All Articles