Ask Ethan: how small are the elementary particles?

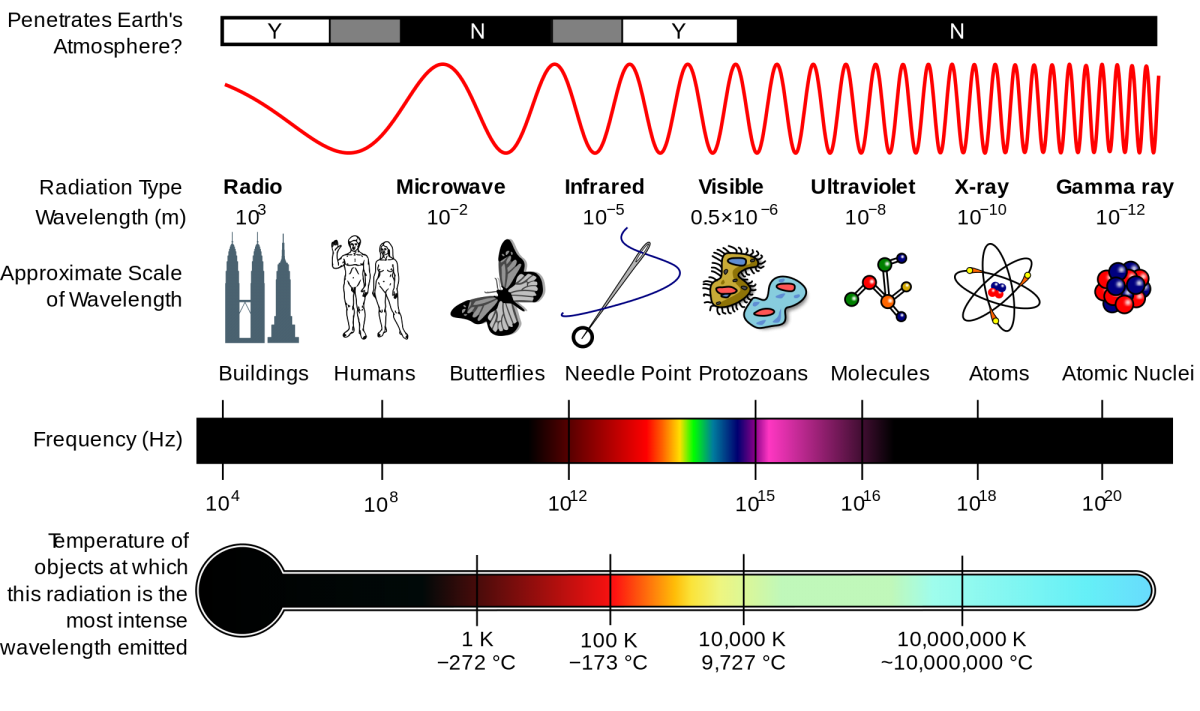
Size, wavelength and temperature / energy scale corresponding to different parts of the electromagnetic spectrum

If you take any amount of matter, arbitrarily small or large, then about its composition there will be only two possibilities: either it can be divided into something smaller, or it is fundamental and indivisible. For most of the 19th century, we believed that atoms were those very fundamental, smallest entities, since the Greek word ἄτομο literally means "uncut". But now we know more, and we can divide atoms into nuclei and electrons, and nuclei can be divided not only into protons and neutrons, but they can also be divided into more fundamental quarks and gluons. But how do we even know their "size"? Our reader asks :

What do scientists mean by the size of an elementary particle?
')
Size is a complex concept, but quantum mechanics hastily help us.


Pentacene molecule through an atomic microscope IBM with a resolution of 1 atom

The image above was made by a method that is not very different from a regular photo - and this is a photo of individual atoms inside a relatively simple molecule. The fact that light is a wave allows you to take photographs of objects of a certain size, but not anything that is arbitrarily small in size. Light has a specific wavelength, so it can interact with something that is approximately equal to or greater than this length, but not less. That is why:

• We need relatively large antennas to capture radio waves, since their wavelengths require antennas of considerable size.
• The holes in the microwave door do not allow the waves to go outside - their wavelengths are larger than the sizes of the holes.
• Why tiny grains of dust in space can perfectly block short-wave (blue) light, block longer waves (red) worse, and are completely transparent for even longer waves (infrared).


On the left - the visible range, on the right - the infrared photo of the Barnard 68 globule

To measure the sizes of the smallest particles, photons of smaller and smaller wavelength are required. Since the photon energy and its wavelength are inversely proportional to each other, you need more and more energy to look at smaller scales.



But using photons is not the only option. It is possible to use any high-energy particles to probe the size of matter. One of the fun rules of quantum mechanics is that not only particles of light, but also all particles in general - including such components as protons and invisible (for now) like electrons, can behave like waves. Having reached high energies and having collided with a fixed target, we can either determine the size of a particle that is not fundamental by observing its decay, or determine that if a particle is not fundamental, it will demonstrate this property only at sizes smaller than a certain .



This technique allowed us to determine that:

• Atoms are not indivisible, they consist of electrons and nuclei with dimensions of about 1 Å, or 10 ^-10 m.
• The nuclei can also be split into protons and neutrons, the size of which is about 1 fm, or 10 ^-15 m.
• And if you bombard particles inside protons and neutrons - quarks and gluons - with high-energy particles, they do not show any internal structure, like electrons.

For each of the particles of the Standard Model, we determined that if they have a composite nature, or have a physical size that differs from a point, then this size should be no more than 10 ^-19 m.



It may not seem strange to us, but there was a time when people were not familiar with quantum mechanics, but the equation E = mc ² was familiar. If we accept that the electron has just such a charge, how it was measured, and that its potential electric energy is responsible for its mass, then we can calculate its size - this quantity is known as the classical electron radius. It turned out that this is a rather small value:



But we already know that it is not. This value turned out to be much larger than the proton size, by about three orders of magnitude. In other words, the particles that we find turn out to be truly quantum in nature, which means that if we rise to arbitrarily high energies, then truly fundamental particles must be pointlike.



So, when we argue about the size of elementary particles, we are talking about the search for something truly fundamental. Are the particles of the Standard Model indivisible? If so, we should be able to rise to higher energies and not detect anything that differs from the behavior of point particles, up to the Planck energy, that is, to scales of the order of 10 ^-35 . On a smaller scale, physics no longer makes sensible predictions, but we continue to approach them. Perhaps along the way we will find that some (or all) of these particles can be broken into others, or that they consist of strings or membranes, or that they are just points. But everything that we know today with regards to the real size of particles refers to particles that are not fundamental. All the rest is only the upper limits, and the search for ways of approaching smaller scales continues.