Ask Ethan: Can gravitational waves allow us to look into a black hole?

Since the LIGO experiment for the first time directly discovered gravitational waves emitted by merging black holes, scientists have renewed their interest in studying these objects. With the help of new data, new techniques and a new way of studying the Universe, we can stand on the threshold of a whole range of new discoveries that have now become possible. One of the fundamental properties of a black hole, of course, is that nothing can leave the event horizon from the inside, since the escape velocity exceeds the speed of light. But perhaps this restriction can be circumvented? The reader wants to know if we have a way to look inside the black hole:

If the space-time distortion can increase the speed of light, is it possible for a gravitational wave passing through the event horizon to give us a way to observe the contents of the black hole, slightly accelerating with?

Let's look at the physics of this process and find out!



You have probably heard that the speed of light in a vacuum, the universal constant s, is a constant. In the special theory of relativity, this is a strict truth. If your space is completely flat, this restriction does not get around. Theoretically, you can arrange an infinite number of fixed observers at equal distances from each other. When a light wave moves past them, the amount of time required for each next observer to see a light signal will be the same. It takes exactly the same amount of time for a passage from the 1st observer to the 2nd one, but from the 2nd to the 3rd, from 3 to 4, from 99 to 100. There are no discrepancies, ambiguities, everyone is happy.
')


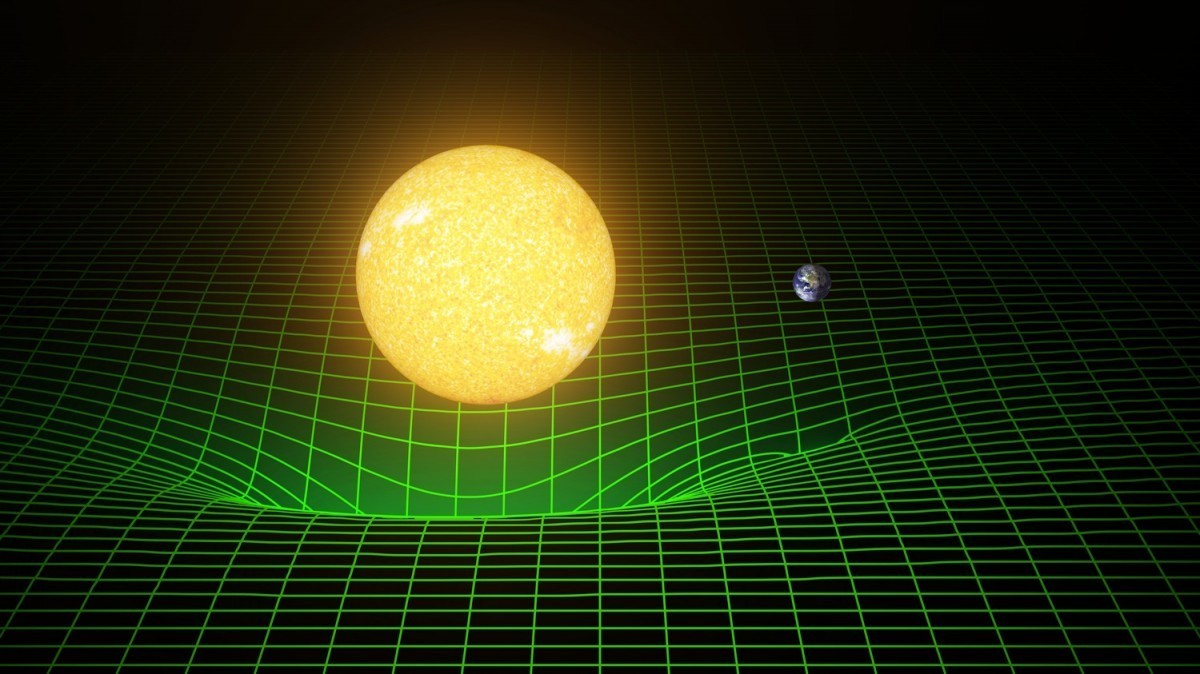
But if you allow space-time to bend, then everything will become much more complicated - this is the big difference between the special and general theory of relativity. If you arrange an infinite number of the same dormant observers at equal distances from each other, they will begin to argue among themselves. Not about any personal differences, but about the differences in their observations regarding the meanings of the words "fixed distance" and "peace." When the light signal passes by them, they all determine its speed, equal to, as expected - but they cannot agree with each other about what happens in other places, not where they stand. There is no common standard for rulers and clocks that apply equally to all observers, if you allow space to bend.


The clock on top of the tower of the Abraj al-Beit complex goes a few quadrillionths of a second faster than the clock at its foot due to differences in the gravitational field.

For the same reason, if you place an atomic clock at the foot of the building, and the other watches are at the top of the building, you will see that they run at a slightly different speed. This does not mean that the clock is wrong - just a non-zero curvature of space leads to the fact that different observers do not agree with each other about the accuracy of the time measurement in any place except where they are.



When the light signal passes through a portion of the curved space, the remote observer may calculate that the signal moves faster or slower with, depending on how much the observation portion is curved compared to the observer portion. But does anything move faster or slower with? No, we just often cannot measure the speed of anything elsewhere than where we are. Einstein noted this in his book from 1920, “Relativity: a special and general theory,” which is translated from German:

According to the general theory of relativity, the law of the constancy of the speed of light in a vacuum, which is one of the two fundamental assumptions of the special theory of relativity, cannot be infinitely reliable. The curvature of light rays can occur only when the speed of propagation of light changes from one place to another.

What about the passage of a gravitational wave? It turns out that it will affect all the space through which it passes. Gravitational waves compress space in one direction, simultaneously stretching it in a perpendicular, in oscillation mode — this is precisely what the LIGO experiment used to detect waves — so they will compress and stretch the black hole event horizon.



The energy of the wave passing inside the horizon of BH events will be absorbed by the black hole. Just as any light falling into a BH will add mass to it (energy is converted into mass according to the less well-known form of the famous Einstein equation, m = E / c ² ), so will it be with gravitational radiation. But unabsorbed waves can distort space, and curved space and the changes occurring in it, will definitely affect the time of passage of light. In gravitational waves, particles perceive time differently; the space looks longer or shorter, depending on the physics of the passing waves; the shapes of physical objects and non-physical geometric structures are distorted.



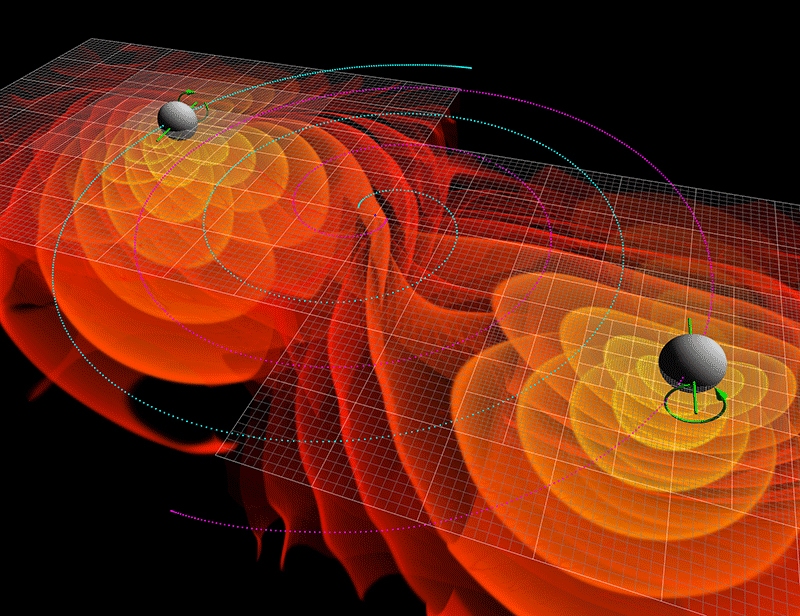
But this does not mean that the space that was inside the event horizon may be outside. A particle from the inside can not get out. At no time can anyone get information about what is happening inside the event horizon, being outside it. The speed of escape on the event horizon will remain equal to c, and what you can call a “change in the speed of light” for an external observer (unable to measure speed in any place other than your own) can be more accurately described as a distortion of the curvature of space.



The space inside the event horizon can expand and / or contract when a gravitational wave passes, but the best you can hope for is a photon that could fall into the hole under other conditions, but could not get there because of the wave. Gravitational waves do not change the fundamental and inevitable nature of BH: nothing that gets inside cannot escape.