Ask Ethan # 106: Where exactly was Newton wrong?

We know that Einstein’s general theory of relativity replaced the Newtonian theory of gravity, but where exactly did Newton make a mistake?

For me, there has never been a higher honor or recognition than those associated with the development of science.
- Isaac Newton

Every week, you send me your questions and suggestions for the weekly column “Ask Ethan.” Sometimes these are speculative questions about the future, sometimes these are questions about the large-scale structures of the Universe or the smallest particles. Sometimes these are questions about the cosmos or the limits of our knowledge. This week, I was interested in the question of Francois Sinsserling about the longest existing physical theory and its failure:

Einstein's general theory of relativity stands above Newton's laws. We understood that. What I would like to know: with the approach of Newton, there is a discrepancy between the precession of the orbit of Mercury. And what do we observe? According to Newton is more or less gravity? Or is the problem somewhere else?



The orbit of every planet in the solar system passes around the sun. It is not an ideal circle, but an ellipse that Kepler noticed almost a hundred years before Newton. The orbits of Venus and Earth are very close to circular, while Mars and Mercury are more elliptical, their minimum distance to the Sun is very different from the maximum.
')
Specifically, Mercury has aphelion (the farthest point from the Sun) is 46% farther away than perihelion (the closest position to the Sun). At Earth, the difference is only 3.4%. This fact is not related to different theories of gravity; just the conditions in which these planets were formed led to such properties of their orbits.



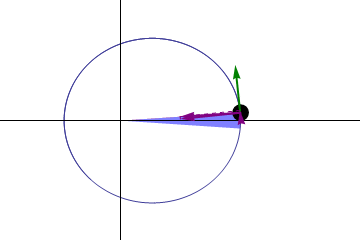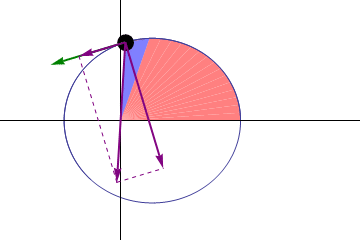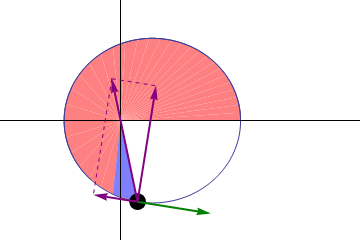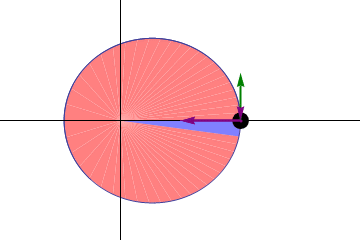
But the fact that these orbits differ from ideal circles means that you can learn something interesting from them. If Kepler’s laws were perfect, then a planet orbiting the sun would have to return to the same point after each revolution. If we have reached perihelion in any year, and then counted out exactly a year, we should also be in perihelion, and we can expect from the Earth that it will fall exactly in the same point in space - relative to the other stars and the Sun, as last year .

But Kepler's laws cannot be ideal, for they apply to massless bodies revolving around massive, in the absence of the rest of the masses. But this situation does not describe our solar system at all.



We have a bunch of massive bodies - planets, moons, asteroids - except for a single planet in orbit around the sun. In addition, the measured planets themselves also have a mass, so they rotate around not the center of the Sun, but the common center of mass of the planet / Sun system. And finally, the Earth has another unpleasant property: the precession of the axis, leading to the presence of a difference between how we celebrate the year (the tropical year related to the seasons and the calendar) and the return of the Earth to the same position in space (the star year related to complete orbit).

And all these features must be taken into account in order to predict changes in the orbits of other planets. What can we expect, having received all the knowledge that we have, on Earth, Mercury and all the rest of the masses that we have detected and measured?



For example, the difference between the star and tropical years is small, but important: the star year is longer by 20 minutes and 24 seconds. This means that we mark the seasons, equinoxes and solstices on the annual calendar, but our perihelion is gradually shifting relative to it. If the circle consists of 360 °, then from January 1 of one year to January 1 of the next we go through only 359.98604 °, which means that the perihelion of each planet shifts by 5025 "every century (in one degree 60 ', angular minutes, and in one minute - 60 ", angular seconds). And this shift looks like an advance in orbit.

But it is necessary to take into account the planetary masses.



Each planet affects the motion of another planet in different ways, depending on the distance between them, their masses and the proximity of the orbits, as well as on which orbit is inside which one. For Mercury, the innermost of the planets, the calculations are the easiest to carry out: all other planets will be external for him, and therefore all of them lead to the advancement of the perihelion forward. Here are the results of the influence of these planets, in descending order of importance:
• Venus: 277.9 "per century.
• Jupiter: 153.6 "per century.
• Earth: 90.0 "per century.
• Saturn: 7.3 "per century.
• Mars: 2.5 "per century.
• Uranus: 0.14 "per century.
• Neptune: 0.04 "per century.

Other effects, including the presence of mass at Mercury itself, the movement of the Sun relative to the center of mass of the Solar System, the contribution of asteroids and Kuiper Belt objects, the non-sphericity of the Sun and planets, contribute not more than 0.01 "per century that can be ignored.



All these effects contribute to 523 "per century, and in total we get 5557" per century, adding the precession of the earth's axis. But if we look at the dimensions of what is actually happening, we’ll get perihelion advancing by 5,600 "per century. This was already known at the end of the 19th century thanks to the incredible observations of Tycho Brahe, originating as early as the 16th century! Such small deviations can be made see if observe for 300 years.

Precession exceeds Newton's predictions; the question is why. There are several hints to answer if you know where to look for them.



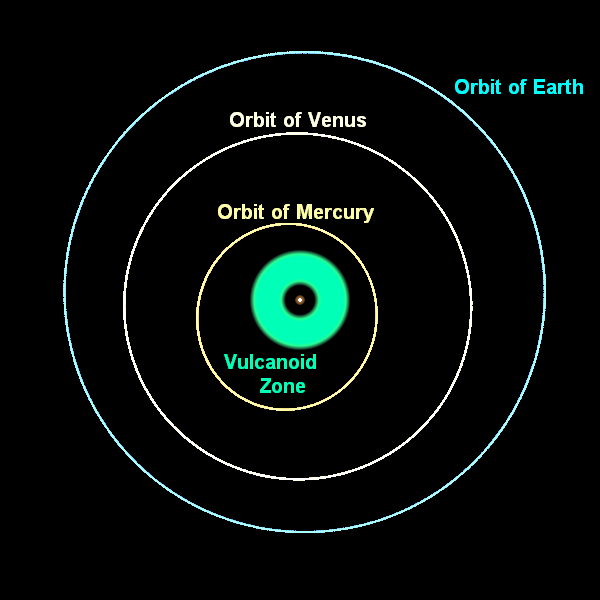
First, it was decided that there is another planet inside the orbit of Mercury, and its characteristics lead to this effect - or that the solar corona is very massive. But the Sun's crown was not massive, and no planet Vulcan (and we were looking for it) does not exist - so these versions were deleted.

The second idea was expressed by two scientists, Simon Newcomb and Asaph Hall [Simon Newcomb and Asaph Hall], who determined that if we replace Newton's inverse square law, stating that gravity decreases with distance in proportion to its square, to another law with a degree of 2,0000001612, then this precession fits into the calculations. Today we know that such an assumption would not correspond to the observable orbits of the Moon, Venus, Earth - so this was also deleted.

The third hint was made by Henri Poincaré, noting that if we take Einstein’s HUNDRED - given that Mercury moves around the Sun at a speed of 48 km / s, or with 0.016% of the speed of light - you can find part of the lost precession (but not all of it).



The combination of the second and third ideas led to the general theory of relativity. The idea of ​​the existence of the space-time fabric was expressed by one of Einstein's former teachers, Hermann Minkowski, and Poincare’s application of this concept to the problem of the orbit of Mercury was an important step towards finding a solution. And the idea of ​​Newcomb Hall, albeit an incorrect one, showed that if gravity were indeed stronger than Newton had predicted, this would lead to a lack of precession.

Einstein's idea was that the presence of matter / energy leads to a curvature of space, and that the closer you are to a more massive object, the more gravity behaves. In addition, the more pronounced are the deviations from Newtonian gravity.



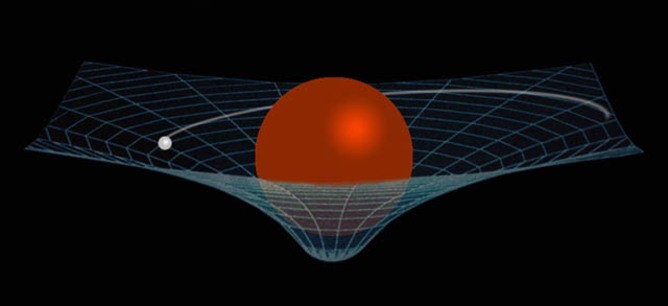
And here it is, the answer to the question of Francois - but this is not the end of the story. When Einstein developed his theory enough to predict additional precession, the result of his calculations — an additional 43 ”per century — was first deemed excessive. At that time, the Newtonian contribution was incorrectly calculated and estimated at only 38” per century. This argument was used to challenge GR.

To verify which theory was correct, it was necessary to predict the curvature of light passing by a massive body.



The theory of Newton predicted that the starlight does not deviate at all, passing by the Sun, because it has no mass. But if we assign the mass to the light on the basis of Einstein E = mc ² , or m = E / c ² , we can find that the light must deviate by 0.87 "when it passes by the outer edge of the Sun. And Einstein's theory predicted twice as much deviation: 1, 75 "

The numbers were small, but the joint expedition of Arthur Eddington and Andrew Crommelin [Arthur Eddington and Andrew Crommelin] during the eclipse of the sun in 1919 was able to take measurements with the desired accuracy. They received a deviation of 1.61 ″ ± 0.30 ″, which, within the margin of error, coincided with Einstein's predictions, and not with Newtonian ones. Newton's theory of gravity has failed.



This is the whole story of how Newtonian gravity was replaced, and why. Since then, GR has had many victories (and no defeats), but in all cases where the Newtonian and Einstein theories differ, the winner — with stronger gravitational effects near massive bodies — is Einstein. Science strides forward, but sometimes the steps take a lot of time!