^{Source of the image.}

Is there a connection between the three-eyed toad and neural networks? What is common between a program winning a go and the Prisma application that redraws photographs under the styles of paintings by famous artists? How did computers beat backgammon, and then encroached on the sacred - and won a man in “Space invaders”?
We will give answers to all these questions, and also talk about the revolution associated with deep learning, thanks to which a breakthrough has been achieved in many areas.

About the authors:

Sergey Nikolenko, mathematician, computer scientist, employee of the Mathematical Logic Laboratory of the St. Petersburg Branch of the Mathematical Institute of the Russian Academy of Sciences, Internet Research Laboratory of the National Research University Higher School of Economics, Kazan Federal University and the Deloitte Analytics Institute, also known as the player of the “What? Where? When?". Sergey is engaged in research, practical development and teaching in the field of machine learning and data processing, network algorithms, theoretical informatics and cryptography. The work of Sergey Nikolenko was supported by the grant of the Russian Science Foundation 15-11-10019.
')
Artur Kadurin, head of the audience segmentation group in the advertising department of the Mail.Ru Group, head of the student laboratory of the Technosphere project at VMK MSU. Arthur analyzes data from various Mail.Ru Group services, including using machine learning technologies.

The most interesting object in the universe

In many areas, the human brain still knows more than a computer. For example, we better deal with natural language: we can read, understand and study the book meaningfully. And in general, we are well able to learn in the broad sense of the word. What exactly does the human brain do and how does it manage to reach such heights? What is the difference between what neurons do in the brain and what transistors do in the processor? This subject is, of course, completely inexhaustible, so let us give only a couple of local examples.

As is known, every neuron from time to time sends an electric impulse along the axon, the so-called spike . As long as the neuron is alive, it never stops and continues to give signals. But when the neuron is in the “off” state, the frequency of the signals is small, and when the neuron is energized, it turns on, the frequency of the spike discharge greatly increases.

The neuron works stochastically: it produces electrical signals at random intervals, and the sequence of these signals can be very well approximated by a random Poisson process . Computers also have gates, exchanging a signal with each other, but they just do it not at all accidentally, but with very tight synchronization; The “processor frequency”, which has long been measured in gigahertz, is the frequency of such synchronization. Each cycle gate of the same level sends a signal to the next level, and they do it even though several billion times a second, but strictly simultaneously, as if on command.

However, very simple observations show that, in fact, neurons are well able to synchronize and very accurately detect very small periods of time. In particular, the simplest and most vivid illustration is stereo sound. When you go from one side of the room to the other, you can, relying solely on the sound from the TV, easily determine the direction to it (and the ability to determine where the sound comes from was just crucial for survival in prehistoric times). To determine the direction, you note the difference in time from which the sound comes to the left and right ear. The distance between the inner ears is not too large (20 centimeters), and if you divide it by the speed of sound (340 m / s), you get a very short interval in the arrival of sound waves, a few tenths of a millisecond, which nevertheless neurons perfectly notice and allow determine the direction with good accuracy. That is, in principle, your brain could work as a computer with a frequency measured in kilohertz; given the enormous degree of parallelization achieved in the architecture of the brain, this could lead to quite reasonable computing power ... but for some reason the brain does not.

By the way, about parallelization. The second important note about the work of the brain: we recognize a person's face in a couple of hundred milliseconds. Moreover, the connections between individual neurons are activated for tens of milliseconds, that is, in the full recognition cycle there can be no consecutive chain of calculations longer than several pieces of neurons - most likely there are less than a dozen. The brain, on the one hand, contains a huge number of neurons, but, on the other hand, it is arranged flat compared to a conventional processor. The processor has very long sequential execution chains, which it processes, and in the brain, sequential chains are short, but it works in parallel, because neurons are lit at once in many places of the brain when they begin to recognize a face and do many other exciting things.



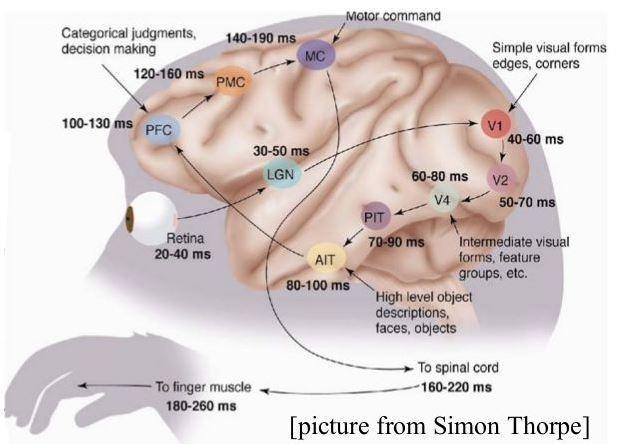
The illustration shows how the processing of the visual signal takes place in time. Light enters the retina, where it is converted into electrical impulses and after 20-40 milliseconds the “image” is transmitted further. The first level of processing takes 10–20 milliseconds (in the picture, time is shown on a cumulative total, that is, for example, only 140–190 ms passes before issuing a command to the motor system). At the second level of processing, after another 20-30 milliseconds, the signal arrives at the neurons that recognize simple local forms. Then another level, another level, and here at the fourth level we already see intermediate forms: you can find neurons that “light up” when they see squares, color gradients, or other similar objects. Then a couple of levels of neurons, and now, after 100 milliseconds from the beginning of the process, we have already lit neurons that correspond to high-level objects. For example, if you met a person, you have a neuron in your brain that is responsible for his face (we are not ready to vouch for this statement, but most likely it is); moreover, a neuron or a group of neurons most likely appears, “responsible” for this person as a whole and triggered by any contact with him, including writing, when the face is not visible. If you see the face again (and the neuron doesn’t unravel back, “forgetting” the old information), then in ~ 100 milliseconds that neuron is activated in your head.

Why does the brain work that way? The simplest and non-explanatory answer to this question is “it happened”. During the evolution of the brain was formed in this way, and this was enough to solve evolutionary problems. In the rationalist community , they say this in the following way : living beings are not fitness-maximizers, which optimize a certain objective survival function, but adaptation-executers, which execute the once randomly chosen “sufficiently successful” solutions. Well, it so happened that a hard synchronization with the built-in metronome was not formed, and why this is so - we are not ready to answer.

In fact, it seems to us that the question “why?” Is really not quite appropriate here, and it is better, more interesting and more productive to ask the question “how?”: How exactly does the brain work? We do not know for sure, but at the level of individual neurons, and in some places and groups of neurons, the processes occurring in our head can already be described quite well now.

What else you need to learn from the brain is the extraction of features (feature extraction, feature engineering). The brain is perfectly able to learn and summarize on a very, very limited sample of data. If you show a small child a table and say that it is a table, then the child will quickly begin to call other tables also tables, although they would seem to have nothing in common: one round, another square, one on one leg, the other on four. It is quite obvious that the child does not do this with the teaching method with the teacher, he clearly would not have enough training sets for this; we can assume that the child first appeared in the head a cluster of “objects on the legs on which things are placed”, then the brain extracted, so to speak, the Platonic eidos of the table, and then heard the word that calls it, and simply marked the finished idea with this in a word.

A small lyrical digression: this process goes, of course, in the opposite direction; Although at the mention of Whorf with Sapir, many linguists are beginning to nervously twitch not only neurons, it must be admitted that many ideas, especially abstract ones, are in many ways socio-cultural constructs. For example, any culture has a word that is similar in meaning to “love,” but its content may be very different, our “love” is not at all like the ancient Japanese. Since the physiological basis of all people is generally the same, it turns out that the abstract idea of ​​“craving for another person” arising in the brain is not simply labeled, but is actively corrected and constructed by the texts and cultural objects that define it for humans. But we digress.

The other side of the issue is neuroplasticity. Scientists have been experimenting to find out how different parts of the brain can easily learn to do things for which they would not seem to be intended. Neurons are the same everywhere, but, in principle, there are areas in the brain that are responsible for different things. There is a Broca zone responsible for speech, there is a zone responsible for vision, and so on. However, we can violate conditional biological boundaries.



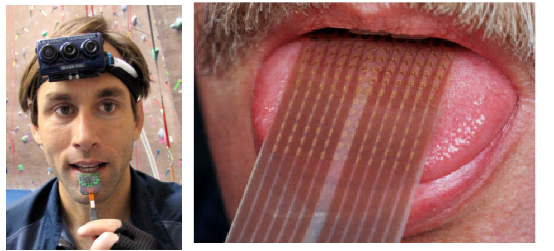
This person learns to see the language . He attaches electrodes to his tongue, hangs a camera on his forehead, and the camera translates an image pixel-by-pixel onto electrodes that tingle the tongue. A man catches such a thing on himself, walks with it with his eyes open for several days. The part of the brain that receives signals from the tongue begins to think: this is very similar to what comes from the eyes. If after a week of bullying eyes tie, then the person begins to really see the language. The person recognizes the form, does not stumble on the wall.



In this photo, a man turns into a bat. He walks blindfolded and uses the sonar, the signals from which are transmitted through the skin to tactile neurons. And also in a few days a person develops echolocation abilities. We do not have a special organ that recognizes ultrasound, we need to attach an external locator, but we learn to process information without problems, that is, we can walk in the dark and not bump into walls.



And here the third eye was implanted in the toad. At first, the toad was a little like three-eyed, then the other two closed to her, and she began to enjoy the third one perfectly.

The brain can adapt to a very large number of new data sources. That is, it turns out that the brain has a kind of “single algorithm” that doesn’t care what is being served, it extracts meaning from it. This single algorithm is the holy grail of modern artificial intelligence; We believe that deep learning is the closest to it from what has been done so far.

However, of course, one has to be careful in asserting whether all of this is really similar to what the brain is doing. A very bright recent work “ Could a neuroscientist understand a microprocessor ?” Is trying to track how modern neuroscience could have done to analyze some very simple “brain” —say, a simple processor from Apple I and Atari, which launches that very Space Invaders game, to which we will return. In detail now we will not tell about it, but we recommend reading the article. Spoiler: neurobiology failed nothing ...

Feature extraction

Unstructured information (text, pictures, music) is processed as follows: there is a raw input , then signs are obtained from it that carry meaningful information, and then classifiers are built on these signs. The hardest part of this process is to understand how to isolate good signs from an unstructured input. Until recently, systems for processing unstructured information looked like this: people diligently tried to manually invent good signs, evaluating what they did, according to the quality of already quite simple regressors and classifiers built on them.

As an example, consider Mel Frequency Cepstral Coefficients ( MFCC ), or chalk-frequency cepstral coefficients, which are often used as a characteristic of speech signals. In particular, the MFCC is used for speech recognition, and in 2000 the European Telecommunications Standards Institute defined a standardized MFCC algorithm for use in cellular communications. Up to a certain point, hand-picked signs dominated machine learning. For example, in the image processing, SIFT (Scale Invariant Feature Transform) was used everywhere, which allows you to isolate features of the image that are resistant to various kinds of transformations and rely on duplicate search or classification based on them.

In general, many signs have been invented, but we still cannot repeat the success of the brain. There is no biological predestination in the human head - there are no neurons that are genetically created, only for speech, there are no neurons that are “accustomed” only to memorizing people, and so on. It seems that any part of the brain can learn anything. Whatever the brain, we would very much like, of course, to learn how to isolate signs automatically; in order to make complex AI, large models in which there are neurons connected with each other for transmitting signals combining any information, most likely there will not be enough human forces for manual development of signs.

Artificial Neural Networks

When Frank Rosenblatt proposed his linear perceptron , everyone began to imagine that the machines were about to become truly intelligent. For the late 1950s, it was very cool that the network itself was learning to recognize the letters in the photographs. Around the same time, neural networks of many perceptrons, which are trained by the backpropagation algorithm, appeared (this is a gradient descent method with a slight modification, called the back error propagation method ). The backpropagation algorithm is, in fact, a way to calculate gradients, that is, derived errors.

Ideas for automatic differentiation appeared as early as the 1960s, but British informatist Jeffrey Hinton rediscovered backpropagation for wide use - one of the key researchers in the revolution of deep learning. By the way, Hinton's great-great-grandfather was George Boole himself, one of the founders of mathematical logic.

Multilevel neural networks appeared in the second half of the 1970s. There were no technical obstacles: take a network with one layer of neurons, then add a hidden layer of neurons, then another one - this is how a deep network is obtained in a simple way, and backpropagation on it, formally speaking, works the same way. Further, these networks began to be used for speech and image recognition, recurrent networks began to appear, networks with regard to time, and so on. But by the end of the 1980s, it turned out that there were several significant problems with the training of neural networks.

The first is to say about the technical problem. In order for the neural network to do something reasonable, there must be a good iron in the base. In the late eighties and early nineties, work in the field of speech recognition by neural networks looked like this: let's change the training parameter and launch the network to study for a week. Then we will look at the result, once again change the parameters and wait another week. This, of course, was a very romantic time, but since the neural networks set up the parameters almost more important than the architecture itself, for a good result on each specific task it took too much time or too powerful hardware.

Now let’s touch on the substantive problem: backpropagation formally really works, but only formally. For a long time, it was not possible to effectively train neural networks with more than two hidden layers due to the problem of vanishing gradients (vanishing gradients) - when calculating the gradient (the direction of the greatest increase in network error in the weighting space), the back propagation method decreases as it passes from the output layer network to the input. The inverse problem — exploding gradients — manifests itself in recurrent networks. If you start to deploy a recurrent network, it may happen that the gradient goes into hatching and will grow exponentially. More details about these problems are written, for example, in the article “ Pre-training of a neural network using a limited Boltzmann machine ”.

Ultimately, these problems led to the second “winter” of neural networks, which lasted throughout the 1990s and the beginning of the 2000s; As John Denker, one of the neural network classics, wrote, “neural networks are not the best continuation of this phrase:“ ... and genetic algorithms are the third ”. But ten years ago there was a real machine learning revolution. Jeffrey Hinton and his group invented a way to properly train deep models. deep belief networks , , .



? , . , , , . , ? . - , . , , — . , , backpropagation . … , , - . , backpropagation, ; 1990- ( ), , . ( ) , .

, . , ( ) GPU ( ). , . , , , ; , , CEO NVIDIA .

? ? 1991 , , , . . , , , , , , , , .

, , , . , , , , , 2, 3, — 4 . - : , , . “ ”, (). — , ( : , ). , . ; Goodfellow, Bengio, Courville “Deep Learning” , , , , :



, . : , , backpropagation. , - .

— . , , - , . autoencoder ().

— , , , . , , .


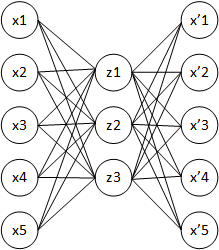
^{x', x}

— , . , ( ).

. , , , , , . , (undercomplete autoencoders) , . , , overcomplete autoencoders, , , . , , , — - 0. , , .




, , , . , . — ( denoising autoencoder ), . . , (, , ) — , .




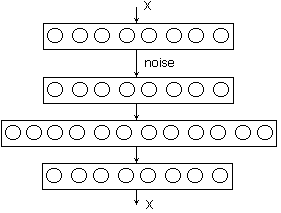
“” , , . , , , ( !). , , — X. , : , , , .

, . , , . , , 0 1 , . , , . “” , , . , , , , “” , “” .



, , . , , . , , , , : , , , “” .

- , - ? . (dropout; , ). , , . - , : . , , , “” .



, . - . “” , , .

: , , , , . ; , .

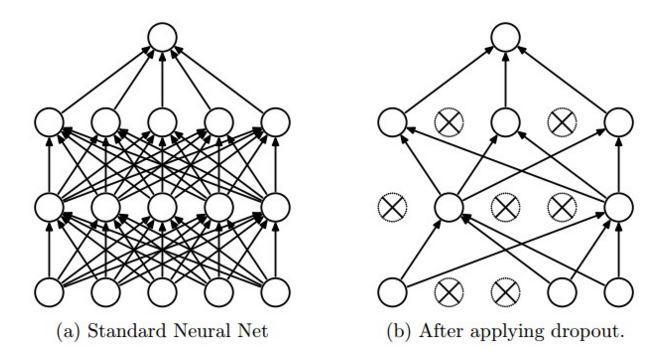
, , , , . ? , 0 1 —1 1. , , ½. ? , ½, , . , , . , , . , , . Nothing like? : . , , — . , , , , , .

. , , unsupervised pre-training . , , ( ).

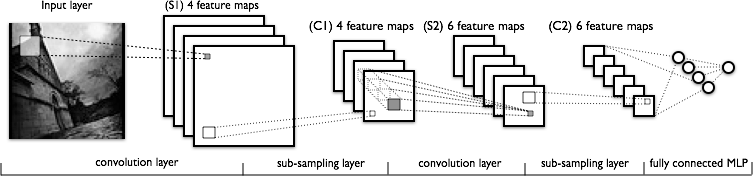
. (convolutional neural network, CNN) 1998 . , :

,
f — , g — () .

, , , . , -, , . , , . , , , . , , .

:

1. , ,
2. , - ,
3. ().

, , — (mean, max, min...) . , , , ; (max-pooling). , .

. , Prisma, ( Mail.Ru Group), . . , scene labeling — , , , . , , — .



And, of course, convolutional networks are used in AlphaGo, which we wrote about last time .

Reinforcement training

Usually, machine learning tasks are divided into two types: supervised learning - this is when the correct answers are given and you need to learn about them, unsupervised learning - when questions are given, but no answers. In real life, it's not like that. How does a child learn? When he comes to the table and hits his head against him, the brain receives a signal that the table is a pain. Next time (well, or through one) the child will not knock his head on the table. In other words, an active study of the environment takes place, in which the correct answer is not given in advance: there is no a priori knowledge in the brain that the table is pain. In addition, the child will not directly associate the table with pain (for this to happen, we usually need special external engineering of neural connections, something like in “A Clockwork Orange”), rather a specific action in relation to the table, and over time will transfer this knowledge to a more general class. objects, for example, on large hard objects with corners.

Experimenting, getting results and learning from it - this is learning with reinforcement . The agent interacts with the environment, performs actions, the environment encourages him for these actions, the agent continues to perform them. In other words, the objective function is presented as a reward, and at each step the agent, being in some state S, chooses some action A from the existing set of actions, and then the environment tells the agent what award he received and in what new S 'state turned out to be.

One of the problems with reinforcement training is to not accidentally retrain to perform the same action in similar states. Sometimes we may mistakenly associate the reaction of the environment with our immediate preceding action; This is a well-known “bug” in the program of our brain, which diligently searches for patterns even where there are not and cannot be. The famous American psychologist Berres Skinner (one of the fathers of behaviorism; it was he who invented the famous Skinner box for mocking mice) put this experiment on pigeons: he put the pigeon in a cage and at equal (!) Intervals did not depend on time poured into the cage feed. In the end, the pigeon decided that receiving feed somehow depended on his actions. For example, if immediately before feeding the pigeon flapped its wings, then in the future he tried to get food for himself in this way - by waving his wings. This effect was later called the “ dovish superstition ”; a similar mechanism probably leads to human superstition.

The above problem is the so-called exploitation vs exploration dilemma, that is, on the one hand, it is necessary to explore new opportunities, study the environment so that it can find something interesting. On the other hand, at some point you can decide: “I have already researched, and I already understand that the table is painful, and sweetie is tasty, and I can go on and get candy, and not try to sniff to that what lies on the table, in the hope that it is even tastier. "

There is a very simple, but no less important example of the reinforcement training task - multiarmed bandits. The meaning of the metaphor is that the agent is “sitting” in a room in which there are several slot machines. The agent can throw a coin into the machine, pull the handle, and as a result, the machine will give him some winnings. Each machine has its own expectation of winning, and the optimal strategy is very simple: it is enough all the time to pull the handle of the machine with the highest expectation. The only problem is that the agent does not know which automaton has what kind of expectation, and his task is to select the best automaton for a limited number of attempts. Or at least “good enough” - it is clear that if several automata have very close expectations of winning, then they are difficult and probably will not need to be distinguished. In this task, the state of the environment is always the same: although in some life applications the probability of getting a gain from a particular automaton may vary with time, in our formulation this does not happen and it all boils down to finding the optimal strategy for choosing the next pen.

Obviously, it is not possible to always pull the most advantageous pen on average, because if we accidentally get lucky on a highly dispersive, but on average completely unprofitable, machine at the very beginning, we will not lose tears from it for a long time. At the same time, the most profitable automaton may not give a big win in the very first few attempts, and then we can only get back to it very much and not very soon.

Good strategies for multi-armed gangsters are built on different implementations of the principle of optimism with uncertainty. This means that if there is a sufficiently large uncertainty in our knowledge of the machine, we will interpret it in our favor and explore further, always reserving to ourselves, albeit with a small probability, to double-check our knowledge about pens that seemed to us unprofitable.

The objective function in this problem is often the cost of learning (regret). This is how much the expected income from your algorithm is less than the expectation of winning at the optimal strategy, when the algorithm simply immediately with divine intervention realized which handle the “thug” had is correct. It turns out that for some very simple strategies one can prove that they optimize the price of education among all strategies in general (up to constant factors). One of these strategies is called UCB-1 (Upper Confidence Bound), and it looks like this:

Pull the handle j, for which the maximum value
,
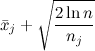Where - the average income from the handle j, n - how many times we pulled all the handles, and n _j - how many times we pulled the handle j.

Simply put, we always pull the handle with the highest priority, where priority is the average income from this handle plus an additional member, which on the one hand grows with the game time to periodically go back to each handle and check if we missed anything she, on the other hand, decreases each time we pull this pen.

Despite the fact that the task of multi-armed bandits in the base case does not imply a transition between states, it is from UCB-1 that the algorithms used for searching the go tree in the tree of moves, with which AlphaGo won a historic victory, originate.

And now let's get back to the training with reinforcement with several states. There is an agent, there is an environment, and the environment gives the agent a reward at every step. The agent wants to get, like a mouse in a maze, more cheese, and less current discharges. In contrast to the problem of multi-armed bandits, the expected “winnings” now depend not only on the currently selected action, but also on the current state of the environment, that is, from the point of view of the agent, on the history of the actions performed by them. In general, in an environment with several states, it turns out that a strategy that brings maximum profit “here and now” will not always be optimal, as it may lead to less favorable conditions of the environment in the future. Thus, we come to maximizing the total profit for all time instead of finding the optimal action in the current state (more precisely, we are still looking for the optimal action, of course, but the optimality will now be determined differently).

From the point of view of total profit, we can estimate every state of the environment. We introduce the concept of the state value function (value function) as a prediction of the total reward after visiting the state. The state value function can be specified, for example, as follows:

,
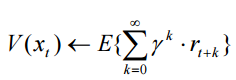where r _t is the immediate reward received when the system is transitioned from the x _t state to the x _{t + 1} state, and γ is the discount factor (0 ≤ γ ≤ 1).

Another variant of the value function is the Q-function, the argument of which is not only the state, but also the action. This is the same as the state value function, but with a higher “level of detail”: the Q function estimates the expected gain, provided that the agent performs this action in the current state.

The essence of reinforcement learning algorithms is often that the agent form the utility function Q based on the reward received from the environment, which later will enable him not to accidentally choose the strategy of behavior, but to take into account the experience of the previous interaction with the environment.

Deep Q-Network

In 2013, Mnich and co-authors published an article in which one of the standard reinforcement learning methods is used in combination with deep neural networks for playing console games Atari.

TD-learning (temporal difference learning, TD-learning) is usually used in contexts where the reward is the result of a fairly long sequence of actions, and the problem is also to distribute the candy along the moves and / or states of the environment that led to it. For example, the same game can go on for several hundred moves, but the model will get a candy for winning or an electric shock for losing only at the very end when the result is known; which moves from your hundred were good and which were bad are a big question, even when the result is known. It is possible that in the middle of the game you stood to lose, but it turned out that the enemy was wrong and you won. And no, trying to artificially introduce “intermediate targets” like “winning material” is a bad idea, practice shows that an opponent can easily take advantage of the inevitable defects of such a system.

The main idea of ​​TD-training is to reuse the already-trained estimates of “late” states close to “candy” as goals for training previous states. We start with random (quite delusional) assessments of the state in the game, but then after each game, the following process takes place: the result in the final position is well known; let's say we won, and the result is +1 (hooray!). We pull up the assessment of the penultimate position to one, the last one - to this last but one, which was pulled to one, and so on. If you study long enough, in the end we will get good grades for each state.



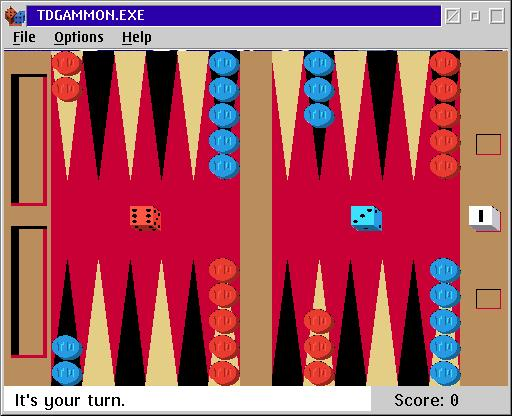
The first great success of this method in games was achieved in the backgammon program TD-Gammon . Backgammon for the computer turned out to be quite a simple game, because there are cubes in them. Since the cubes fall in different ways, there is no big problem with where to get training games or a reasonable opponent, which will allow you to explore the entire space of possible games: you can just send the program to play against yourself, and the randomness built into backgammon will allow you to explore quite widely and .

TD-Gammon was developed about 30 years ago; however, even then the basis of the program was made up of the neural network. The position from the game was submitted to the network input, and the network predicted the assessment of this position, that is, the probability of victory. After each batch of the program against itself, a set of test examples was obtained, new for the network, the network was trained on them and continued to play against itself (or slightly earlier versions of itself).

TD-Gammon beat all people in the late eighties, but it was believed that this was due to the specificity of the game of backgammon due to the presence of dice. However, it turned out that deep learning helps computers to win in many other games. For example, recently happened to the already mentioned Atari games. The difference between the experiment and backgammon or even chess was that in the console game no one explained the rule models in advance. All that was known to the computer is an image, the same as a person would see it, and points scored (this must be asked explicitly, otherwise it would be incomprehensible than to win better than to lose). The computer, in turn, could perform one of the actions available on the joystick - turning the joystick itself and / or pressing a button.


^{About 200 attempts by the car took to “figure out” the essence of the game, another 400 to get the skill, and now the computer wins at the 600th race.}

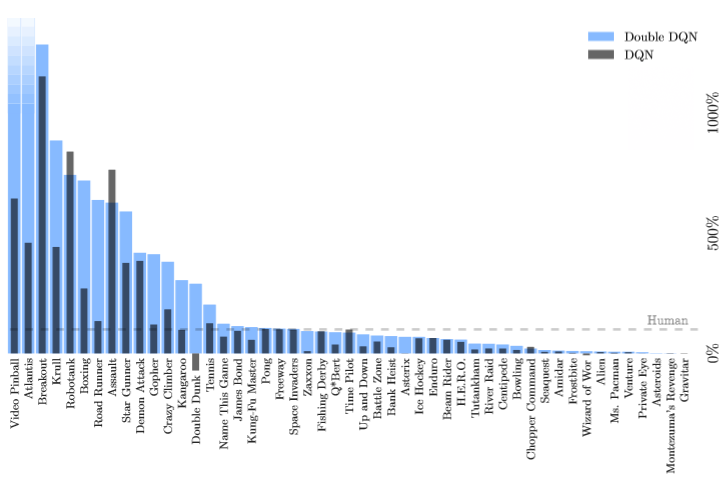
Here, Q-learning is also used, we are also trying to build a model that approximates the function Q, but now the deep convolutional network is considered as this model. And it turned out that it works great. In 29 games, including such hits as Space Invaders, Pong, Boxing and Breakout, the system was generally better than humans. Now the team from DeepMind, responsible for this development, is engaged in games from the 1990s (the first project will probably be Doom). There is no doubt that they will cope in the very near future and will go further - to the present.

Another interesting example of using the Deep Q-Network model is solving the paraphrase problem. You are given a sentence, and you want to write it differently, but at the same time convey the same meaning. A little artificial task, but it is very closely connected in general with the task of creating text. In the recently proposed approach for this approach, the LSTM-RNN ( Long Short-Term Memory Recurent Neural Network , a type of recurrent neural network) chain, which is called an encoder, is taken and the text is folded into a compact vector representation. Then the compact representation is developed in the sentence from the other side by a similar chain - the decoder. Since it is decoded from a minimized representation, then, most likely, the proposal will be different. This process is called encoder-decoder architecture . Machine translation works in a similar way: we fold the text in one language, and then expand it with approximately the same models in another language, assuming that the internal hidden representation in the semantic space is common. So, it turned out that Deep Q-Network can iteratively generate different sentences from the hidden representation and different decoding options, in order to bring it closer to the original sentence over time. The behavior of the model is quite reasonable: in the experiments, DQN first fixes the parts that we have already well rephrased, and then goes on to the difficult parts, on which the resulting quality is still so-so; in other words, the DQN is substituted for the decoder in this architecture.

What next?

Modern neural networks are getting smarter from day to day. The deep learning revolution took place in 2005–2006, and since then interest in this topic has only grown, every month and almost every week there are new works and new interesting applications of deep networks appear. Recently, we have witnessed the tremendous success of the Prisma and Mlvch applications , which have forced us to write about neural networks, even those that do not specialize in publishing technology. In this, we hope, quite popular article we tried to explain what the place of the deep learning revolution of the last ten years was in the general history and structure of the development of neural networks, which, in fact, was done, and dwelt on learning with reinforcement and how deep networks can learn to interact with the environment.

Practice shows that now, at the stage of explosive growth of deep learning, it is quite possible to create something new, exciting and solving real problems of people literally “on the knee”, only a modern video card is needed (perhaps yes), enthusiasm and desire to try. Who knows, perhaps it is you who will leave a mark in the history of this ongoing “revolution” - in any case, it’s worth a try.