Ask Ethan # 31: Why are we made of matter?

If at the beginning of the Universe existence there was an equal amount of matter and antimatter in it, why does matter dominate in today's space?

You may not feel very powerful, but if you are a medium-sized adult, your modest body contains at least 7 × 10 ¹⁸ J of potential energy — it would be enough so that you could explode with a power of thirty very large hydrogen bombs if you would know how to free her and if you really needed it.
- Bill Bryson

At the end of the week, I choose the best of your questions for the “ask Ethan” column, and this week the honor is given to Justin Starr, who asks:

As I understand it, in the emerging universe there were equal parts of matter and antimatter, as a result of which serious annihilation took place. And how does matter conquered as a result?

Justin asks about one of the greatest unsolved mysteries of the universe.
')
Think of these two seemingly contradictory facts:


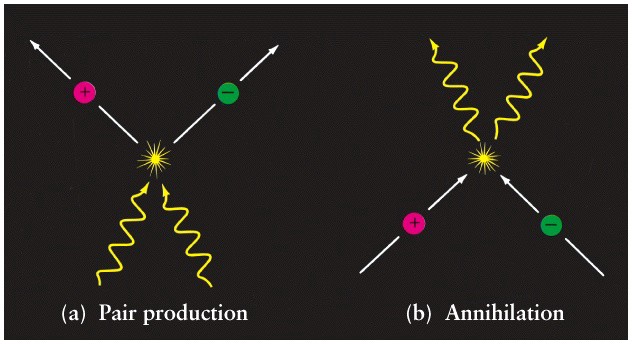
a) creating a pair; b) annihilation

1) None of the interactions of particles observed by us with any level of energy created or destroyed a single particle of matter without creating or destroying an equal number of antimatter particles. The physical symmetry between matter and antimatter is even more strict:

• each time, creating a quark, we create and antiquark
• every time a quark is destroyed an antiquark is destroyed
• every time we create or destroy a lepton, we create or destroy the antilepton of the same family, and
• each time a quark or lepton experiences interaction, collision or decay, the total number of quarks and leptons at the end of the reaction (quarks minus antiquarks, leptons minus antileptons) remains the same as it was at the beginning

The only way to add or subtract matter in the Universe is in a way that reduces or adds antimatter in the same quantities. But there is a second fact:



2) When we study the Universe, stars, galaxies, gas clouds, clusters, superclusters, structures of the largest scale - everything looks created from matter, not from antimatter. Every time matter and antimatter occur in the Universe, an incredible release of energy occurs due to the annihilation of particles.

In some places we observe this annihilation, but only near hyper-energy sources that produce matter and anti-matter in equal amounts. When antimatter collides with matter in the universe, it produces gamma radiation of very specific frequencies that we can detect.

But if we look at the space between the stars and between the galaxies, even on a large scale, we will find that there is a lot of material there, even if there are no stars there. Cosmos is great, and the density of matter is small, so you can ask yourself - if you throw one particle of antimatter (say, an anti-proton), how long will it last, on average, before it hits a particle of matter and annihilates.



In the interstellar space of our galaxy, the average lifetime of a particle would be 300 years, which is very short compared with the age of the galaxy. This restriction means that at least within the Milky Way, the amount of antimatter that can fit among matter is one part per 10 ¹⁵ ! ..

On large scales, the order of galaxies and galactic clusters, the constraints are not as strong, but still quite serious. Observing space at distances from several million to three billion light-years, we found a deficiency of x-rays and gamma rays, which should arise from the annihilation of matter and antimatter. We see that even on a cosmic scale, 99.999% of everything that exists is made up of matter, like us, and not of antimatter.



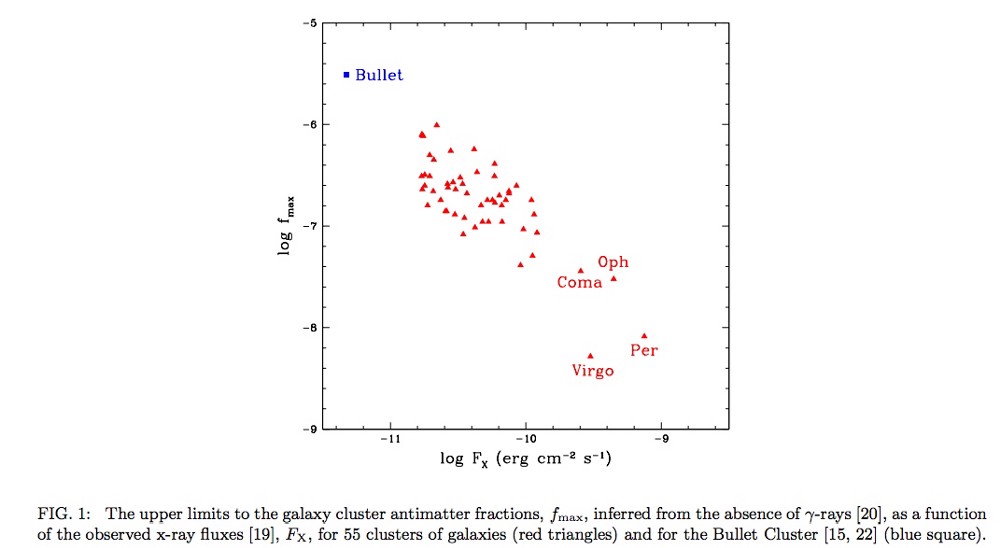
And this is only a lower estimate of the level of matter dominance over antimatter in the Universe, according to observational data.

So, on the one hand, we have the results of experiments that demonstrate the impossibility of creating and destroying matter without concomitant destruction and creating the same amount of antimatter, and on the other, we have a Universe which, as far as we can judge, consists of almost 100% of matter and almost 0% antimatter. What the heck?

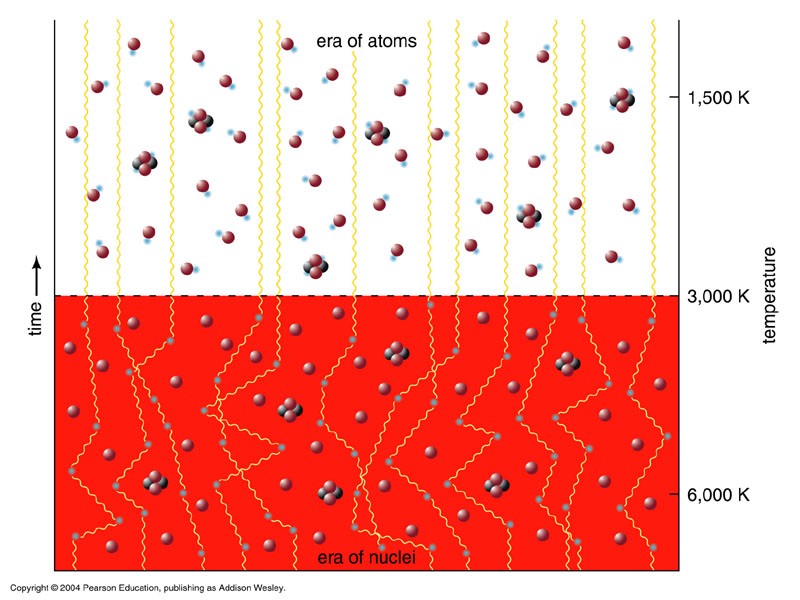
If we want to understand how this happened, we need to go back to the very origins of the Universe, by the time immediately after the end of inflation and the Big Bang: by the time when the Universe was hot, dense and full of matter, antimatter and radiation.



In the early stages of the universe, everything was hot and dense. The part that now constitutes the observable part of the Universe consisted of 10 ⁹⁰ particles of matter, antimatter and radiation, while the amount of matter and antimatter was the same. There was so much energy that in any collision of particles they could spontaneously generate the same amount of matter and antimatter, and when matter and antimatter collided, they turned into radiation. And this happened all the time and everywhere.



If the Universe could only create matter and antimatter vapors so that they could annihilate again, our Universe would look quite different today. Theoretically, if there were no symmetry of matter and antimatter, with the cooling and expansion of the Universe, we would have reached the moment when it would be impossible to create a new particle. Existing pairs of matter and antimatter would annihilate until space would become so sparse that particles could not find each other, and we would have a universe filled with photons and a small amount of matter and antimatter.

How many would be left? As far as we know, approximately 10 ⁷⁰ particles of matter and antimatter, and photons would be 10 ²⁰ times more than protons. That is, for each proton there would be 100,000,000,000,000,000,000 photons, and there would be as many antiprotons as protons.

But we can measure the ratio of the number of photons to protons.


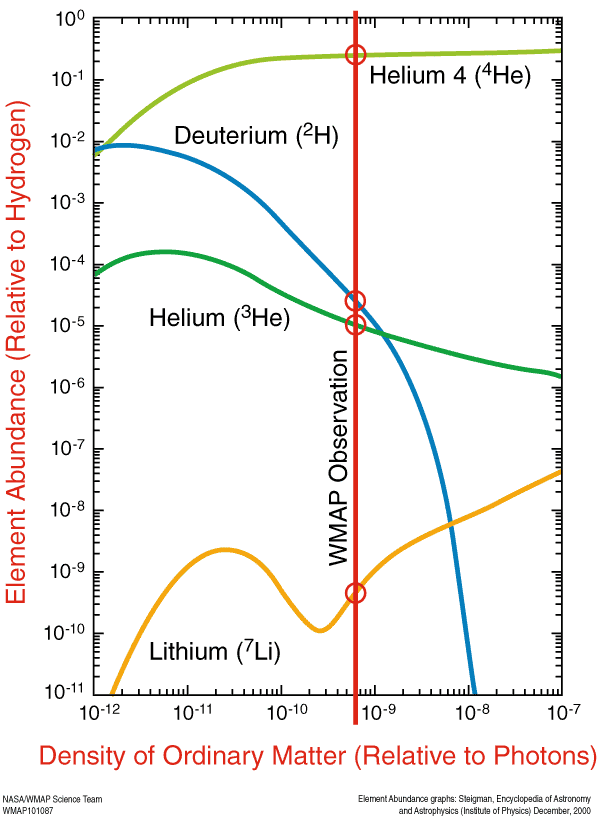
Vertical: the number of elements relative to hydrogen; horizontal: density of ordinary matter relative to protons

It is not such a terrible asymmetry. Of course, there are many, many times more photons than protons, but the ratio is more like a couple of billions to one (and almost without antimatter), which indicates an incident in the early Universe that created the fundamental asymmetry of matter and antimatter. As far as we can see, asymmetry happened everywhere and with the same power.



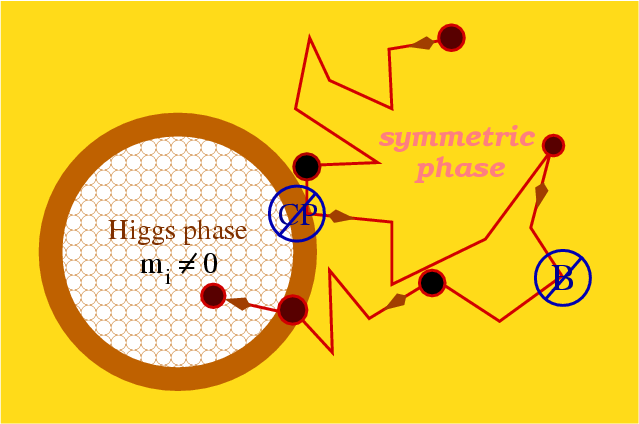
If you want to know exactly how this happened - welcome to the club. This is the problem of baryogenesis, and it is one of the greatest unsolved problems in fundamental physics. But just from the fact that we do not know exactly how this could happen, it does not follow that we do not have a worthy general idea of ​​how this happened. Specifically, Andrei Sakharov showed that if three conditions are satisfied, then an asymmetry of matter and antimatter can be created from the initially symmetric state:

• nonequilibrium conditions
• C and CP symmetry breaking
• interactions with violation of the law of conservation of baryon numbers

That's all. Only three things. And as far as we know, in the Universe they all should be.



Nonequilibrium conditions. It's simple. If you have a large, hot, expanding and cooling Universe, governed by the laws of GR and quantum field theory, congratulations: your conditions are non-equilibrium. Equilibrium is when all particles in the system have the ability to communicate with each other, or exchange information. But in an expanding cooling universe, particles from one edge have no causal relationships with particles from another. In a very early universe there were 10 ⁵⁰ unrelated regions, where even the light would not have enough time to pass from one region to another.

The early Universe was not only in a disequilibrium state, it would be very difficult for you to design a system that was in a less balanced state.


The parity of elementary particles is determined by the direction in which they emit decay particles. Muon usually emits an electron to the right. With inverse parity, the muon should emit an electron to the left. Once out of a thousand, anti-muon disintegrates to the right, which breaks CP symmetry

Violation of C-and CP-symmetry. C-transformation or charge conjugation (the operation of replacing a particle with a corresponding antiparticle), and P - parity (a mirror image of everything). Roughly speaking, C and P are preserved if you fix each of these symmetries, and at the same time the laws of physics are preserved; and CP symmetry is preserved if you simultaneously fix both symmetries, and all the laws of physics remain unchanged.

In our universe, gravitational, electromagnetic, and strong interactions retain C, P, and CP. But the weak violate them! Specifically, the decay of mesons containing strange quarks and charming quarks strongly violates C, P and CP, that is, there are fundamental differences in the behavior of particles and their antiparticles. There are two conditions out of three.

And finally ...


Proton grandchildren and proton grandfather:
- Grandpa, tell us about the big war in which you participated!
- Sit down, kids, it's a long story. Today it is called baryogenesis, and we call it Hell. It began almost fourteen billion years ago. Soon after the Big Bang, the young Universe cooled enough to cause particles. First came the leptons. They survived their leptonogenesis war. Over these nanoseconds, baryons and anti-baryons formed in equal amounts ...
To be continued...

Interactions with violation of the law of conservation of baryon numbers. This is a complicated thing, since we have never observed the creation of a quark without an antiquark (and a baryon is any particle consisting of three quarks, like a proton or neutron. Quarks exist in nature only in bound states!). But if we look at the Standard Model, we conclude that it should contain this type of interaction.

And now I'm going to show you the field equations governing the Standard Model of particle physics (don't worry about the details).



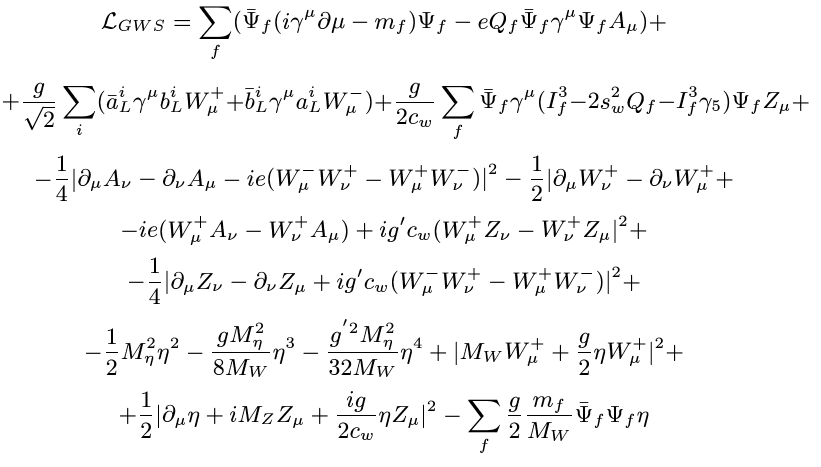
It is important here that this equation has a mathematical “anomaly” necessary for a certain amount of particle decay — for example, for the decay of a neutral pion — and also allowing the violation of the law of conservation of baryon number. Moreover, it allows violations of the law of conservation of both baryonic (for example, proton) and lepton (for example, electron) numbers to occur, but they must be broken together, that is, there must be a constant total number of baryons and leptons in the Universe! This very well explains why there are an equal number of protons and electrons, and, therefore, why the Universe, where protons and electrons exist, is electrically neutral.



Of course, the main question arises when we begin to conduct calculations. If we take into account

how much the Universe is disequilibrium
the number of observed violations of C- and CP-symmetries
how strongly the Standard model violates the law of conservation of baryon numbers

Will we get a sufficiently strong violation of the law of conservation of baryon numbers?



As far as we know today, no, not really. So far, there is a discrepancy of ten orders of magnitude. Of course, in the Standard model, at higher energy levels, there may be much more interactions that violate CP symmetry, which we have not yet discovered, but most often assume that there is physics beyond the Standard Model, which allows more violations of CP symmetry or law to occur. baryon number conservation.



Features include, but are not limited to, the following options:

• Affleck-Dine mechanism based on supersymmetry
• Standard Model additions on electro-weak scales
• leptogenesis, in which the fundamental asymmetry of leptons is created (possibly from a new neutrino physicist), and asymmetry of baryons is already emerging from it
• baryogenesis of scales of the Theory of Great Unification, where a new physics of scales of electroweak association with strong interaction allows us to create more matter than antimatter

Most likely, the meaning of these words is not clear to you, so let me, for example, tell you about the possibility associated with the Theory of Great Unification. Note that this is most likely not the case, and the described scenario is used only for illustration.



Imagine an early Universe filled with radiation and various particles and antiparticles, the last of which exist in equal quantities. Some are quarks and antiquarks, some are leptons and antileptons, some are bosons (and their antiparticles, where applicable; many bosons are antiparticles for themselves), and so on.

Imagine that there is a new kind of charged particles mating with both quarks and leptons. We call them Q-particles.



Initially - just as in the case of particles of matter and antimatter - they are created in a hot, early Universe in pairs. Sometimes Q +, a version of a particle from matter, finds a Q-, a version from antimatter, and they annihilate, and sometimes other particles collide with enough energy to create Q + / Q- pairs.

So all this happens (for a small fraction of a second), and then the universe cools down. Suddenly, new Q + / Q- pairs cease to appear, and after a part of the Q + / Q- pairs annihilate and turn into radiation, the remaining unstable particles will disintegrate.



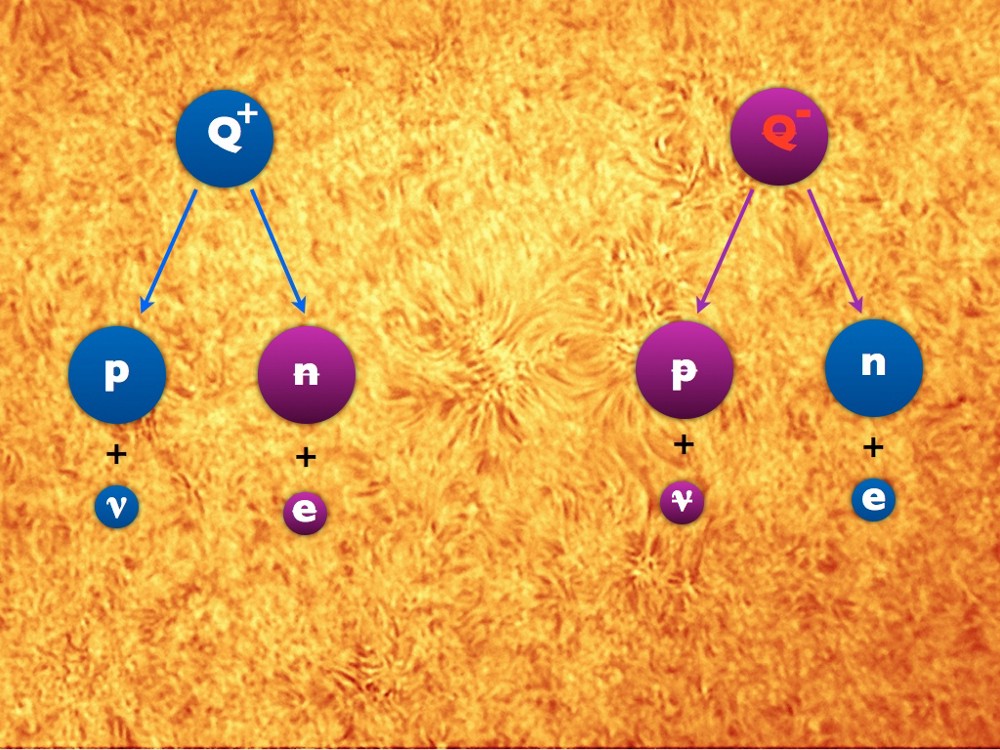
According to the laws of elementary particle physics (even allowing for extensions of the Standard Model), some symmetries should be preserved. The particles Q + and Q- should be the same:

• lifetime
• decay paths
• charge, mass and number “baryons minus leptons”

In this example, the Q + and Q- particles have the same average lifetime, the number of “baryons minus leptons” is zero, and although Q + can decay into a proton and neutrino, or an anti-neutron and anti-electron, Q- can decay into an antiproton and antineutrino, or neutron and electron. These processes violate the law of conservation of baryon numbers and lepton numbers, but not “baryons minus leptons”. Such a scenario is possible and reasonable, but it will not create baryon asymmetry if we do not introduce a violation of CP symmetry.



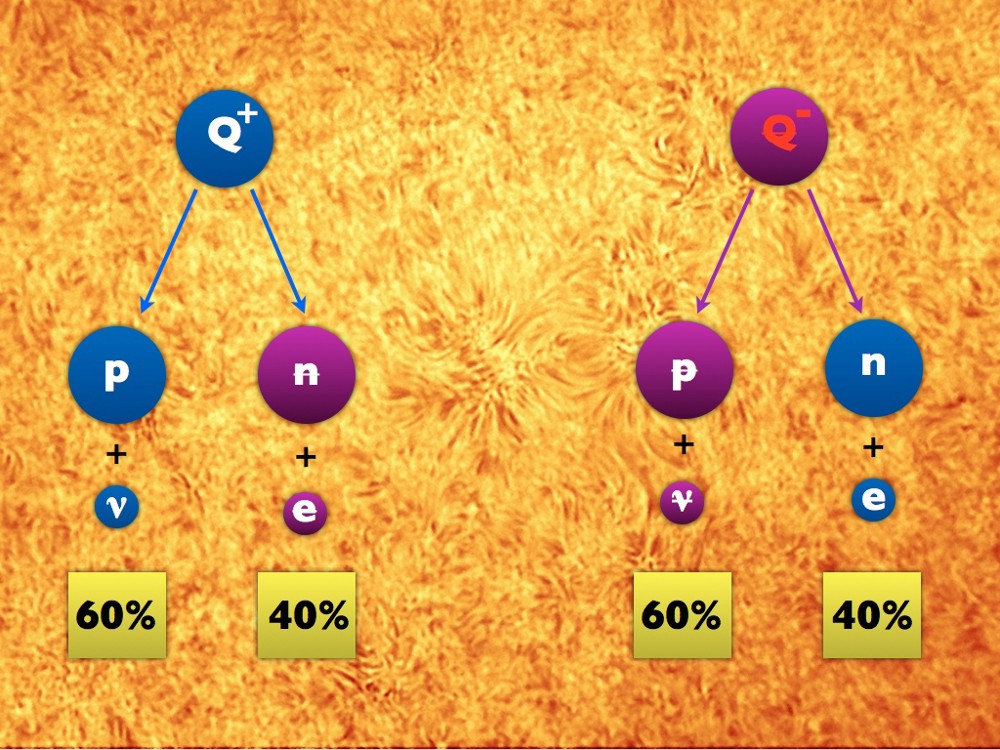
Without this violation, what is called a branch ratio, or proportions in which Q + and Q- fall apart along each path, will be the same. If 60% of Q + decays into protons and neutrons, then 60% of Q- will decay into antiprotons and antineutrinos. Another way may be 40% for both Q + and Q-, which also preserves CP symmetry.

But if you allow its violation, the relationship of branching to particles and antiparticles can be different! As long as the total decay proportions for Q + and Q- are the same, the laws of physics allow this behavior. Let's introduce a violation of CP symmetry.



A small difference: Q + decays again, as before, but Q- is now more decomposed into neutrons and electrons, and less into antiprotons and antineutrinos!

When all the Q + and Q- particles disintegrate (ignoring leptons for simplicity), what do we get?



A bunch of protons, neutrons, antiprotons and antineutrons. Over time, the antiprotons and protons will meet and annihilate, as do neutrons and antineutrons. But due to the asymmetry of the decay of Q + and Q- particles, more protons appeared than antiprotons, and more neutrons than antineutrons.

After the annihilation of all pairs of particles / antiparticles, baryon asymmetry remains. If we follow the lepton asymmetry, we find that there are exactly as many electrons as protons, and the number of neutrinos exceeds the number of antineutrinos by exactly the number of neutrons.

And although this is probably not an accurate description of the mechanism of baryogenesis, something like that most likely happened, and created our present Universe!



These three conditions of Sakharov:

• nonequilibrium conditions
• C and CP symmetry breaking
• interactions with violation of the law of conservation of baryon numbers

unequivocally exist in the Universe, and the only question that remains to be answered is: “how did the asymmetry of matter and antimatter arise that we are observing today?”. The answer I give reflects our current ideas, and I am not ashamed that it is not complete. But of all the great mysteries on the topic “where did it all come from, this, most likely, we can solve even during my life.

Thanks for the great question, Justin, and I hope you enjoyed it. If you have questions, ask them to me, and you can appear in the next article.