Formula Wallis for the number Pi found in the hydrogen atom
In 1655, the English mathematician John Wallis published the treatise Arithmetic of the Infinite, where he derived the formula for the number π from a product of an infinite series of fractions that gradually converge.
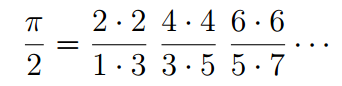
The Wallis formula is not very suitable for practical calculations, but has been useful in many theoretical studies. Now mathematicians from the University of Rochester (USA) suddenly discovered that the same formula is suitable for describing the quantum-mechanical energy levels of a hydrogen atom. This means that there is a direct connection between the real world of physics and the abstract world of pure mathematics.
“We did not specifically look for the Wallis formula for π. She herself fell into our hands, ” says Carl Hagen, co-author of the scientific article" Quantum mechanical formula for π " published in the Journal of Mathematical Physics.
')
"For us, this was a complete surprise - I literally jumped at the moment when we derived the Wallis formula from the equations for hydrogen atoms," his colleague Tamar Friedmann from the University of Rochester admitted. What is important in this - our discovery beautifully combines physics and mathematics. It amazes me how a purely mathematical formula from the 17th century characterizes the physical system, which was discovered only 300 years after its launch. ”
A strange pattern was first noticed by Karl Hagen quite by accident. He solved the problem of calculating the positions of the energy levels of the hydrogen atom with students. For this, special versions of the Schrödinger equation are used. At the same time, the values of energy levels are well known from real experiments.
Together with the students, the teacher noticed that the spread in the predicted and real positions of energy levels followed some mathematical pattern, moving from the lower to the upper levels. For example, the error level for the first level, where the only electron of hydrogen is located, was 15%, for the second - 10% and so on.
Hacken turned to Friedmann, a mathematician by training. He remembered the old formula of Wallis. It turned out that the ratio of the fractions in the formula corresponds exactly to the scatter between the real and calculated values of the energy levels.

In a low-energy orbit, the position of the electron is fuzzy and blurred, and in a more excited state, the orbits become more clearly defined and the error in predicting the position of the electron and the radius of the orbit decreases.
The theory of quantum mechanics was formulated at the beginning of the 20th century, and the Wallis formula has been known for centuries, but no one has seen the connections between them: “Nature has kept this secret for the past 80 years,” says Friedmann. “I'm glad we managed to uncover it.”
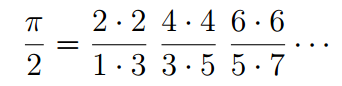
The Wallis formula is not very suitable for practical calculations, but has been useful in many theoretical studies. Now mathematicians from the University of Rochester (USA) suddenly discovered that the same formula is suitable for describing the quantum-mechanical energy levels of a hydrogen atom. This means that there is a direct connection between the real world of physics and the abstract world of pure mathematics.
“We did not specifically look for the Wallis formula for π. She herself fell into our hands, ” says Carl Hagen, co-author of the scientific article" Quantum mechanical formula for π " published in the Journal of Mathematical Physics.
')
"For us, this was a complete surprise - I literally jumped at the moment when we derived the Wallis formula from the equations for hydrogen atoms," his colleague Tamar Friedmann from the University of Rochester admitted. What is important in this - our discovery beautifully combines physics and mathematics. It amazes me how a purely mathematical formula from the 17th century characterizes the physical system, which was discovered only 300 years after its launch. ”
A strange pattern was first noticed by Karl Hagen quite by accident. He solved the problem of calculating the positions of the energy levels of the hydrogen atom with students. For this, special versions of the Schrödinger equation are used. At the same time, the values of energy levels are well known from real experiments.
Together with the students, the teacher noticed that the spread in the predicted and real positions of energy levels followed some mathematical pattern, moving from the lower to the upper levels. For example, the error level for the first level, where the only electron of hydrogen is located, was 15%, for the second - 10% and so on.
Hacken turned to Friedmann, a mathematician by training. He remembered the old formula of Wallis. It turned out that the ratio of the fractions in the formula corresponds exactly to the scatter between the real and calculated values of the energy levels.

In a low-energy orbit, the position of the electron is fuzzy and blurred, and in a more excited state, the orbits become more clearly defined and the error in predicting the position of the electron and the radius of the orbit decreases.
The theory of quantum mechanics was formulated at the beginning of the 20th century, and the Wallis formula has been known for centuries, but no one has seen the connections between them: “Nature has kept this secret for the past 80 years,” says Friedmann. “I'm glad we managed to uncover it.”
Source: https://habr.com/ru/post/368949/
All Articles