Einstein's problem for the programmer

Citylink sent a letter in honor of teacher's day on October 16. The letter contained a reference to the puzzle , having decided which, it was possible to get 50 points equivalent to 50 rubles. There was no time to solve a problem at work, but on Sunday time appeared. It is obvious that the problem is solved on the basis of elementary logic with the use of paper and a pencil with an eraser, but what to do if there is time, and think the head is lazy. At the same time, there is an additional condition: do you have a computer and also go very lazily with a pencil sheet? The author is aware that Einstein had no computer.
The first idea that came to mind is to organize a complete search of options. However, before writing the code, the total number of options was calculated, because I wanted to go through for one evening, and it was necessary to estimate the chances.
We set the task: It is necessary to guess the permutation of the 5x5 matrix, that is, to guess the location of the 25 elements in the matrix. Total number of options: 25! It is better not to take it. But in reality this is not so: only the matrix elements in the rows are subject to permutation, therefore the total number of options: 24,883,200,000 = 5! ^ 5 = 120 ^ 5. But this is already a real number, especially given the fact that while the options are being moved, you can watch the Cross Ange .
We decided to encode.
As a platform, we will choose x64 for one simple reason: we obviously need recursion, but at the expense of ABI on x64 it is a little faster.
We need 3 algorithms:
- The algorithm for generating permutations. Take stackoverflow.
- Matrix printing algorithm and
- We will write the algorithm for checking all the conditions ourselves.
bool CheckMatrix(Terms const *matrix) { bool b = true; for (size_t i = 0; b && i < sizeof(ColConds) / sizeof(*ColConds); i++) { bool c = false; for (size_t j = 0; !c && j < rowLen; j++) { c = c || ColConds[i](j); } b = b && c; } progress++; if ((progress & (1024 * 1024 - 1)) == 0) { printf("%I64u\n", progress); } return b; } The printing algorithm is trivial, and the verification algorithm is a bit more cunningly collected from two overloaded functions, one of which collects recursion, and the second prints progress and checks the current state of the matrix.
We also need an array with conditions, under which, the matrix permutation will be considered suitable for the problem condition:
std::function<bool(size_t)> ColConds[] = { [](size_t column) {return matrix[0 + 1 * rowLen] == DRIVER; }, [](size_t column) {return matrix[2 + 3 * rowLen] == NO; }, [](size_t column) {return matrix[column + 0 * rowLen] == TRI && matrix[column + rowLen * 3] == TABLET; }, [](size_t column) {return matrix[column + 2 * rowLen] == SMART && matrix[column + rowLen * 4] == SNAKE; }, [](size_t column) {return matrix[column + 1 * rowLen] == MANAGER && matrix[column + rowLen * 0] == ODIN; }, [](size_t column) {return matrix[column + 1 * rowLen] == ADVOKAT && matrix[column + rowLen * 2] == TV; }, [](size_t column) {return matrix[column + 0 * rowLen] == STUDIO && matrix[column + rowLen * 2] == EBOOK; }, [](size_t column) {return (matrix[column + 2 * rowLen] == COFFEE && matrix[column + 1 + rowLen * 4] == CAT) || (matrix[column + 2 * rowLen] == COFFEE && matrix[column - 1 + rowLen * 4] == CAT); }, [](size_t column) {return (matrix[column + 1 + 2 * rowLen] == EBOOK && matrix[column + rowLen * 4] == DOG) || (matrix[column - 1 + 2 * rowLen] == EBOOK && matrix[column + rowLen * 4] == DOG); }, [](size_t column) {return matrix[column + 1 * rowLen] == SYSADM && matrix[column + rowLen * 3] == PC; }, [](size_t column) {return matrix[column + 1 * rowLen] == BUILDER && matrix[column + rowLen * 4] == FISH; }, [](size_t column) {return matrix[column + 2 * rowLen] == MULTI && matrix[column + rowLen * 3] == MONO; }, [](size_t column) {return (matrix[column + 1 + 1 * rowLen] == DRIVER && matrix[column + rowLen * 0] == DVA) || (matrix[column - 1 + 1 * rowLen] == DRIVER && matrix[column + rowLen * 0] == DVA); }, [](size_t column) {return matrix[column + 1 + 0 * rowLen] == TRI && matrix[column + rowLen * 0] == CHETIRE; } }; Yes, I was too lazy to invent a name for 14 functions, and therefore I used lambdas. I can also say that in the conditions of the included optimizations, the cost of calling a function by address and via std :: function is about the same, so ... we code as faster.
')
Result under hayd: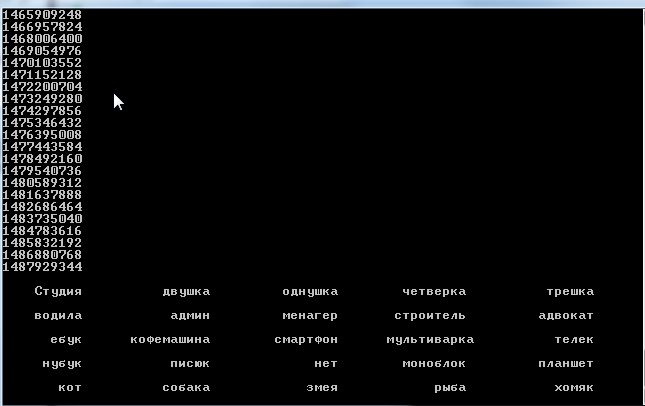

The full text of the program for fans to sort out:
Build as a console application.
// EinstainTask.cpp : Defines the entry point for the console application. #include "stdafx.h" #include <functional> //total task complexity: 24 883 200 000 variants = 120^5 namespace { enum Terms { STUDIO , ODIN , DVA , TRI , CHETIRE, DRIVER , ADVOKAT , MANAGER, BUILDER, SYSADM, MULTI , SMART , EBOOK , COFFEE , TV , PC , MONO , TABLET , NO , NOTEBOOK, CAT , DOG , SNAKE , FISH , HOMA }; TCHAR const * textDB[] = { _T("") , _T("") , _T("") , _T("") , _T(""), _T("") , _T("") , _T(""), _T("") , _T(""), _T(""), _T(""), _T("") , _T(""), _T(""), _T("") , _T(""), _T(""), _T("") , _T(""), _T("") , _T("") , _T("") , _T("") , _T(""), }; Terms matrix[sizeof(textDB) / sizeof(*textDB)]; const size_t rowLen = 5; unsigned long long progress = 0; std::function<bool(size_t)> ColConds[] = { [](size_t column) {return matrix[0 + 1 * rowLen] == DRIVER; }, [](size_t column) {return matrix[2 + 3 * rowLen] == NO; }, [](size_t column) {return matrix[column + 0 * rowLen] == TRI && matrix[column + rowLen * 3] == TABLET; }, [](size_t column) {return matrix[column + 2 * rowLen] == SMART && matrix[column + rowLen * 4] == SNAKE; }, [](size_t column) {return matrix[column + 1 * rowLen] == MANAGER && matrix[column + rowLen * 0] == ODIN; }, [](size_t column) {return matrix[column + 1 * rowLen] == ADVOKAT && matrix[column + rowLen * 2] == TV; }, [](size_t column) {return matrix[column + 0 * rowLen] == STUDIO && matrix[column + rowLen * 2] == EBOOK; }, [](size_t column) {return (matrix[column + 2 * rowLen] == COFFEE && matrix[column + 1 + rowLen * 4] == CAT) || (matrix[column + 2 * rowLen] == COFFEE && matrix[column - 1 + rowLen * 4] == CAT); }, [](size_t column) {return (matrix[column + 1 + 2 * rowLen] == EBOOK && matrix[column + rowLen * 4] == DOG) || (matrix[column - 1 + 2 * rowLen] == EBOOK && matrix[column + rowLen * 4] == DOG); }, [](size_t column) {return matrix[column + 1 * rowLen] == SYSADM && matrix[column + rowLen * 3] == PC; }, [](size_t column) {return matrix[column + 1 * rowLen] == BUILDER && matrix[column + rowLen * 4] == FISH; }, [](size_t column) {return matrix[column + 2 * rowLen] == MULTI && matrix[column + rowLen * 3] == MONO; }, [](size_t column) {return (matrix[column + 1 + 1 * rowLen] == DRIVER && matrix[column + rowLen * 0] == DVA) || (matrix[column - 1 + 1 * rowLen] == DRIVER && matrix[column + rowLen * 0] == DVA); }, [](size_t column) {return matrix[column + 1 + 0 * rowLen] == TRI && matrix[column + rowLen * 0] == CHETIRE; } }; void print() { for (int i = 0; i < sizeof(textDB) / sizeof(*textDB); i++) { if (i % rowLen == 0) _tcprintf(_T("\n")); _tcprintf(_T("%10s\t"), textDB[matrix[i]]); } } bool CheckMatrix(Terms const *matrix) { bool b = true; for (size_t i = 0; b && i < sizeof(ColConds) / sizeof(*ColConds); i++) { bool c = false; for (size_t j = 0; !c && j < rowLen; j++) { c = c || ColConds[i](j); } b = b && c; } progress++; if ((progress & (1024 * 1024 - 1)) == 0) { printf("%I64u\n", progress); } return b; } template<typename T> bool permute(T *v, const size_t start, const size_t n, size_t row); bool CheckMatrix(Terms *matrix, size_t row) { size_t rowCount = 5; if (row == (rowCount - 1)) { return CheckMatrix(matrix); } else { return permute(matrix + (row + 1) * rowLen, 0, rowLen, row + 1); } } template<typename T> void swap(T *v, const size_t i, const size_t j) { T t(v[i]); v[i] = v[j]; v[j] = t; } template<typename T> void rotateLeft(T *v, const size_t start, const size_t n) { T tmp = v[start]; for (size_t i = start; i < n - 1; i++) { v[i] = v[i + 1]; } v[n - 1] = tmp; } // rotateLeft template<typename T> bool permute(T *v, const size_t start, const size_t n, size_t row) { if (CheckMatrix(matrix, row)) return true; if (start < n) { size_t i, j; for (i = n - 2; i >= start; i--) { for (j = i + 1; j < n; j++) { swap(v, i, j); if (permute(v, i + 1, n, row)) return true; } // for j rotateLeft(v, i, n); if (i == 0) break; } // for i } return false; } // permute }; int _tmain(int argc, _TCHAR* argv[]) { for (int i = 0; i < sizeof(textDB) / sizeof(*textDB); i++) { matrix[i] = (Terms)i; } if (permute(matrix, 0, rowLen, 0)) { print(); } return 0; } Build as a console application.
PS: I did not have time to look at the series. Went faster. Feels like the computer did it in 4 minutes.
PPS: Those who want to solve the puzzle on their own, I strongly advise you not to look under the guide.
PPPS: There will be a huge request to all those who say negative, to say, in a personal or in a commentary, what is bad about the article that it is so actively minus. For the first article and you can always fix it.
Source: https://habr.com/ru/post/368697/
All Articles