Ask Ethan # 22: the lack of birthday paradox

There are 364 days when you can get a gift not for a birthday, and only one for birthday gifts, you know.

- Lewis Carroll

The reader asks:

Among my 1434 Facebook friends today, no one has a birthday. What are the chances of such an event, if there are 365.25 days in a year?

Suppose all your friends were born after March 1, 1900.







Over the past 114 years, a leap year has occurred every 4 years. Assuming that all the acquaintances were born on completely random days and years, we get that there are 4 chances out of 1461 that they were born on any day except February 29, and 1 chance out of 1461 that they were born on February 29.

')

Let's calculate the chances that an arbitrary number of your friends do not have a birthday today. Let's start with one.







If you have one friend, and today is not February 29, then the chances that he does not have a birthday are 1,457 out of 1,461, or 99.73%. And this is true for any of your friends.



So, the second friend also has a chance of having a birthday today at 99.73%, and the third, and the hundredth, and so on. For simplicity, let's take 6 friends - what are the chances then that none of them have DR today?







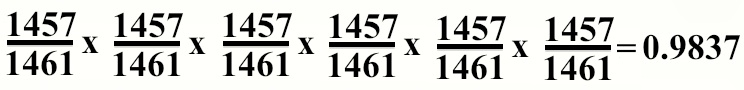
98.37%, because it is necessary that the first person does not have DR, and the second does not, and so on. Otherwise, everything is gone.



The fun is that this formula can be extended to any number of people.

Number of friends	Chances for everyone	Overall odds	In percents
1 friend	0.99726215	(0.99726215) ^ 1	99.73%
2 friends	0.99726215	(0.99726215) ^ 2	99.45%
5 friends	0.99726215	(0.99726215) ^ 5	98.64%
10 friends	0.99726215	(0.99726215) ^ 10	97.30%
50 friends	0.99726215	(0.99726215) ^ 50	87.19%
150 friends	0.99726215	(0.99726215) ^ 150	66.28%
253 friends	0.99726215	(0.99726215) ^ 253	49.98%
365 friends	0.99726215	(0.99726215) ^ 365	36.76%
500 friends	0.99726215	(0.99726215) ^ 500	25.39%
1000 friends	0.99726215	(0.99726215) ^ 1000	6.447%
1434 friends	0.99726215	(0.99726215) ^ 1434	1.961%
1680 friends	0.99726215	(0.99726215) ^ 1680	0.9993%
2000 friends	0.99726215	(0.99726215) ^ 2000	0.4156%
2500 friends	0.99726215	(0.99726215) ^ 2500	0.1055%
3000 friends	0.99726215	(0.99726215) ^ 3000	0.02679%
5000 friends	0.99726215	(0.99726215) ^ 5000	0.0001113%

For a small number of friends, chances are great. They fall to 50-50 after reaching the number of friends in 253 people, and after that they quickly decrease. For 1434 friends, the odds are less than 2%. With 5000 friends, you will get chances of 0.0001113%, or 1 in 900000.



What about a more general approach? If we want to know the odds that there is at least one day in a year when no one has a DR? This is more complicated.







If we count the chances that no one else today has a DR, and subtract it from 100%, then we get the chances that someone else has a DR. To create a situation in which no one has DR, you can subtract from 100% the chances that someone has a DR on any day of the year. This, of course, will only be possible if there are at least 365 friends.

Number of friends	Chances of no DR	Chances of DR	Chances dr every day	Subtract from 100%
365 friends	36.76%	63.24%	(0.6324) ^ 365	100% - 2.3 × 10 ^ -71%
500 friends	25.39%	74.51%	(0.7451) ^ 365	100% - 2.3 × 10 ^ -45%
1000 friends	6.447%	93.553%	(0.93553) ^ 365	99.9999999973%
1434 friends	1.961%	98.039%	(0.98039) ^ 365	99.927%
1680 friends	0.9993%	99.0007%	(0.990007) ^ 365	99.927%
2000 friends	0.4156%	99.5834%	(0.995834) ^ 365	97.44%
2500 friends	0.1055%	99.8945%	(0.998945) ^ 365	31.97%
3000 friends	0.02679%	99.97321%	(0.9997321) ^ 365	9.32%
5000 friends	0.0001113%	99.9998887%	(0.999998887) ^ 365	0.0406%

It turns out that if you have less than 2000 friends, there will be at least one day almost unequivocally in the year when no one has a DR, and if there are more than 4000, then there will be practically no chance for that.