Is it possible to influence the light by the electric field?
It turns out you can. And below I will tell you how. This post was born from my answer to a question asked on the Quora website.

It will be about quantum vacuum. So he looks in the artist's view.
')
redit : lactamme.polytechnique.fr
The question in the original sounds like this:
Or in translation:
Generally speaking, and this is indicated in the responses to Quora, the question is not quite correctly formulated. Light is not a particle, but a wave or (wave-particle duality!) A stream of particles, light quanta — photons. However, this incorrectness does not cancel the question itself. Indeed, if light has an electromagnetic nature, then why could it not be influenced by electromagnetic fields?

Approximately the electromagnetic wave is usually depicted in training courses.
Why I wanted to answer this question is because it, in fact, has a double bottom. There is an obvious answer and an answer that can be given only with certain knowledge that goes beyond the school curriculum.
But first, we agree that the discussion below will deal only with vacuum, since the propagation of light in a medium can be influenced by an electric or magnetic field indirectly through an impact on this medium.
So, the obvious answer: no, it is impossible. Why not, can be explained in different ways depending on how the light is represented.
If we describe light as an electromagnetic wave, the impossibility of affecting it with electromagnetic fields follows from the linearity of Maxwell's equations, which actually describe all electromagnetic phenomena in classical physics. The electromagnetic wave is one of the solutions to these equations, and the external field is another solution. By virtue of the linearity property, their sum is also a solution to Maxwell's equations, and therefore they do not “interfere” with each other and do not have any effect on each other.
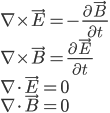
Maxwell equations in vacuum in the SI system
If we describe light as a stream of particles - photons - then the answer is explained by the fact that the photons do not have an electric charge, and the electromagnetic fields act only on charged particles. Interestingly, this situation is unique to electromagnetic interaction. The carriers of the two other fundamental interactions, the weak and the strong, can themselves also take part in the interaction that they tolerate.

Who interacts with in the Standard Model.
Credit: Trush Vitaliy // Wikimedia Commons // CC-BY-SA 3.0
For example, according to quantum chromodynamics, a strong interaction is carried by gluons. They interact between particles that have a so-called color charge - an analogue of the electric charge for strong interaction. In this case, the gluons themselves have a color charge and therefore interact with each other, and with other particles with a color charge.
Let us return, however, to oursheep photons.
I have already noted above that the obvious answer is only the first layer. Let's remove the second one. So, the non-obvious answer is yes, the light can be affected by external fields.
This possibility is connected with the fact that, according to quantum electrodynamics, vacuum, it is also called quantum vacuum, is not an absolute void. Moreover, it is filled with so-called virtual particles, also known as quantum fluctuations. They can be imagined as particles and antiparticles, annihilating pairs, which are born for a short period of time and then immediately, first of all, an electron and a positron.

Picture explaining the idea of quantum fluctuations.
Credit: universe-review.ca
If we continue to describe the quantum vacuum in the form of images, then in the external electric (and magnetic, but only on the electric) field, the virtual pairs begin to live a little longer, since the electric force slightly “pulls them away”. This leads to the fact that the vacuum appears polarization. And where there is polarization, there is also a dielectric constant!
If you remember the school course of optics, then further reasoning for you should be obvious. Indeed, we know that a change in the dielectric constant leads to a change in the refractive index and speed of light, and this, in turn, leads to the refraction and reflection of light.
This effect is, of course, very weak, and to observe it requires absolutely fantastic fields of magnitude. In addition, to observe the refraction of light in such fields would be very difficult because of its insignificance. Despite this, it is now seriously said that in 10–20 years to observe the effect of vacuum polarization on the propagation of light in the laboratory.
It is supposed to use lasers of ultrahigh peak power to generate superstrong fields. Currently, lasers with a power of more than 1 petawatt have been built (peta means a multiplier of 10 15 ), with their help radiation was obtained, the electric field in which reaches values of the order of 10 14 –10 15 volts per meter. This is only 1000 times smaller than the so-called Schwinger limit, at which the effects of quantum electrodynamics in vacuum become noticeable.
However, to observe the effect, it is not necessary to reach the limit, enough fields are ten times weaker. And this means that after only one or two generations of super-power lasers — with powers of about 100 petawatts — in the laboratory will be able to change the direction of light propagation with the help of another light, that is, with the help of electromagnetic fields. However, it is not the direction of propagation that will measure, but the polarization of light. The fact is that a vacuum in a superstrong field acts as a birefringent medium . The velocities of waves with different polarization in such an environment are different, therefore, when an arbitrarily polarized wave propagates in it, its polarization will change and this change is much easier to measure.

It will be about quantum vacuum. So he looks in the artist's view.
')
redit : lactamme.polytechnique.fr
Where does the question come from?
The question in the original sounds like this:
Light is an electromagnetic particle. Can we deviate its path to it?
Or in translation:
Light is an electromagnetic particle. Can we change its trajectory by applying an electric or magnetic field?
Generally speaking, and this is indicated in the responses to Quora, the question is not quite correctly formulated. Light is not a particle, but a wave or (wave-particle duality!) A stream of particles, light quanta — photons. However, this incorrectness does not cancel the question itself. Indeed, if light has an electromagnetic nature, then why could it not be influenced by electromagnetic fields?

Approximately the electromagnetic wave is usually depicted in training courses.
Why I wanted to answer this question is because it, in fact, has a double bottom. There is an obvious answer and an answer that can be given only with certain knowledge that goes beyond the school curriculum.
But first, we agree that the discussion below will deal only with vacuum, since the propagation of light in a medium can be influenced by an electric or magnetic field indirectly through an impact on this medium.
Obvious answer
So, the obvious answer: no, it is impossible. Why not, can be explained in different ways depending on how the light is represented.
If we describe light as an electromagnetic wave, the impossibility of affecting it with electromagnetic fields follows from the linearity of Maxwell's equations, which actually describe all electromagnetic phenomena in classical physics. The electromagnetic wave is one of the solutions to these equations, and the external field is another solution. By virtue of the linearity property, their sum is also a solution to Maxwell's equations, and therefore they do not “interfere” with each other and do not have any effect on each other.
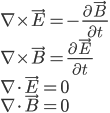
Maxwell equations in vacuum in the SI system
If we describe light as a stream of particles - photons - then the answer is explained by the fact that the photons do not have an electric charge, and the electromagnetic fields act only on charged particles. Interestingly, this situation is unique to electromagnetic interaction. The carriers of the two other fundamental interactions, the weak and the strong, can themselves also take part in the interaction that they tolerate.

Who interacts with in the Standard Model.
Credit: Trush Vitaliy // Wikimedia Commons // CC-BY-SA 3.0
For example, according to quantum chromodynamics, a strong interaction is carried by gluons. They interact between particles that have a so-called color charge - an analogue of the electric charge for strong interaction. In this case, the gluons themselves have a color charge and therefore interact with each other, and with other particles with a color charge.
Let us return, however, to our
Unclear answer
I have already noted above that the obvious answer is only the first layer. Let's remove the second one. So, the non-obvious answer is yes, the light can be affected by external fields.
This possibility is connected with the fact that, according to quantum electrodynamics, vacuum, it is also called quantum vacuum, is not an absolute void. Moreover, it is filled with so-called virtual particles, also known as quantum fluctuations. They can be imagined as particles and antiparticles, annihilating pairs, which are born for a short period of time and then immediately, first of all, an electron and a positron.

Picture explaining the idea of quantum fluctuations.
Credit: universe-review.ca
If we continue to describe the quantum vacuum in the form of images, then in the external electric (and magnetic, but only on the electric) field, the virtual pairs begin to live a little longer, since the electric force slightly “pulls them away”. This leads to the fact that the vacuum appears polarization. And where there is polarization, there is also a dielectric constant!
If you remember the school course of optics, then further reasoning for you should be obvious. Indeed, we know that a change in the dielectric constant leads to a change in the refractive index and speed of light, and this, in turn, leads to the refraction and reflection of light.
This effect is, of course, very weak, and to observe it requires absolutely fantastic fields of magnitude. In addition, to observe the refraction of light in such fields would be very difficult because of its insignificance. Despite this, it is now seriously said that in 10–20 years to observe the effect of vacuum polarization on the propagation of light in the laboratory.
It is supposed to use lasers of ultrahigh peak power to generate superstrong fields. Currently, lasers with a power of more than 1 petawatt have been built (peta means a multiplier of 10 15 ), with their help radiation was obtained, the electric field in which reaches values of the order of 10 14 –10 15 volts per meter. This is only 1000 times smaller than the so-called Schwinger limit, at which the effects of quantum electrodynamics in vacuum become noticeable.
However, to observe the effect, it is not necessary to reach the limit, enough fields are ten times weaker. And this means that after only one or two generations of super-power lasers — with powers of about 100 petawatts — in the laboratory will be able to change the direction of light propagation with the help of another light, that is, with the help of electromagnetic fields. However, it is not the direction of propagation that will measure, but the polarization of light. The fact is that a vacuum in a superstrong field acts as a birefringent medium . The velocities of waves with different polarization in such an environment are different, therefore, when an arbitrarily polarized wave propagates in it, its polarization will change and this change is much easier to measure.
Source: https://habr.com/ru/post/365941/
All Articles