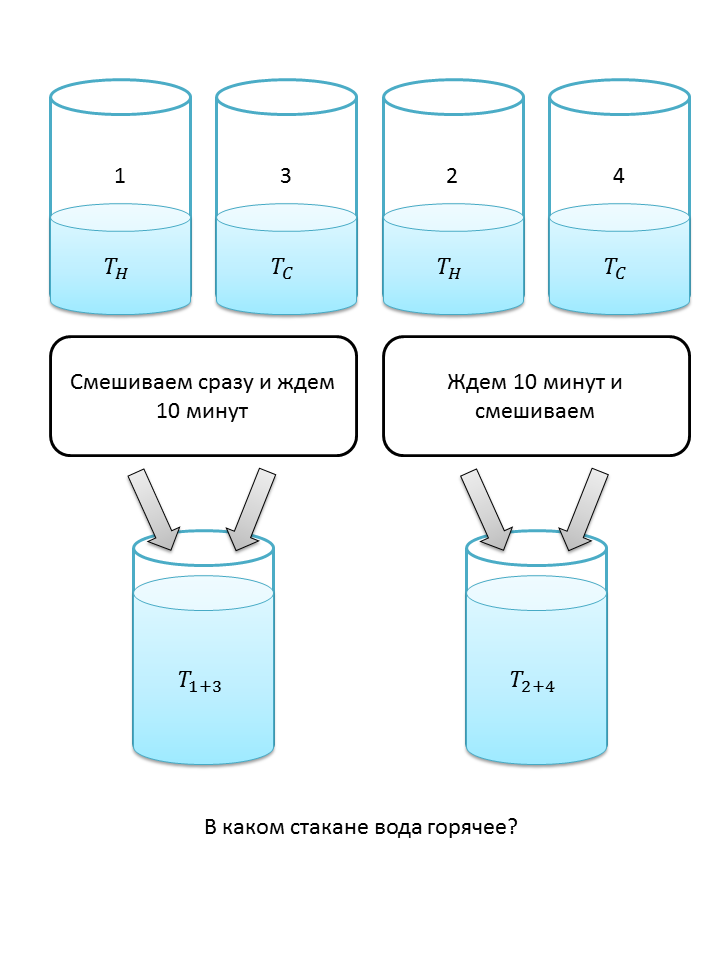
Task about four glasses
In the comments to my post , one of the users asked an interesting question . Its essence is as follows: We have 4 glasses, with the same volume of water. 2 of them are hot and 2 are cold. Mix glasses with hot and cold water. We are waiting for 10 minutes and mix the remaining ones. Question: in which mixture will the water be hot?
Heating and cooling obey the Newton-Richman law , the solution of which has the form:

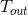 - ambient temperature;
- ambient temperature;
 - initial temperature;
- initial temperature;
 - time;
- time;
 - coefficient described below;
- coefficient described below;
Let's explore this formula in detail:
')
Now a few words about the coefficient :
:

 - heat transfer coefficient, depending on many factors, obtained experimentally.
- heat transfer coefficient, depending on many factors, obtained experimentally.
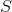 - the area of the interface;
- the area of the interface;
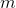 - weight;
- weight;
 - body specific heat;
- body specific heat;
If with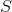 (contact area of water and vessel walls), specific heat capacity
(contact area of water and vessel walls), specific heat capacity  and mass
and mass 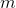 everything is clear, then with the heat transfer coefficient
everything is clear, then with the heat transfer coefficient  everything is not so obvious. It shows how many joules per second will go through the square meter boundary, with a temperature difference of 1 Kelvin. Fortunately, in our case, knowing the absolute value of this coefficient is not important.
everything is not so obvious. It shows how many joules per second will go through the square meter boundary, with a temperature difference of 1 Kelvin. Fortunately, in our case, knowing the absolute value of this coefficient is not important.
What will be the final temperature of the water after mixing? However trite it may sound, but for our case (we mix equal amounts of water):

 - temperature of hot (Hot) water;
- temperature of hot (Hot) water;
 - temperature of cold (Cold) water;
- temperature of cold (Cold) water;
 - mixture temperature;
- mixture temperature;
The temperature of these glasses varies exponentially and over time will be:
will be:
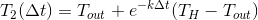

Next, mix and get:


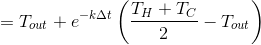
We mix:

And through we get:
we get:

It would seem that there is no difference, but ...
From the point of view of heat loss, our cylindrical glass can be divided into three zones: the bottom (bottom), the upper part (top) and the side walls (sidewall). Therefore, the coefficient can be written as an amount:
can be written as an amount:
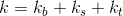 where
where
 ,
,  ,
, 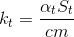
If the glass is considered as a cylinder with a radius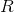 and tall
and tall  , then:
, then:
 , but
, but

We can write:

So, for case 1 and 3, when mixed, the mass and height of the water column doubles:

But this has nothing to do with case 2 and 4, since they cool down (heat up) alone, and after mixing, a further change in temperature does not bother us at all.
If we consider
 and
and

it can be concluded that will always be less than
will always be less than 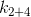 and therefore, if we recall that the coefficient determines the rate of temperature change, it is, in case of 1 and 3, less.
and therefore, if we recall that the coefficient determines the rate of temperature change, it is, in case of 1 and 3, less.
The catch is the meaning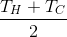 relative to ambient temperature. If this value is higher, then the cooling of the 1 + 3 mixture will be slower than 2 + 4 and, as a result, the temperature of the first will be higher. However, if you adjust the experiment in such a way that the average temperature is lower than the ambient temperature, the 2 + 4 mixture will be “hotter”, since it heats up faster.
relative to ambient temperature. If this value is higher, then the cooling of the 1 + 3 mixture will be slower than 2 + 4 and, as a result, the temperature of the first will be higher. However, if you adjust the experiment in such a way that the average temperature is lower than the ambient temperature, the 2 + 4 mixture will be “hotter”, since it heats up faster.
In fact, this article is a very clear example of the fact that it is impossible to approach practice without a theory. And this paragraph contains conclusions more importantly than the above. Not knowing the fact that the result depends, among other things, on the ambient temperature, will lead to misinterpretation of the latter. Just imagine, two friends set up an experiment, cold water 5 degrees, hot 60. But one of them is at home 25, and the other 40. The results will be inconsistent. And if they also have different glasses or actions are not synchronous ... But much worse, it is false to say about the only correct outcome of the experiment, if the results are the same (due to the fact that hot water is more often "hotter" than cold "cooler" relative to room temperature ). Also, you should always at least approximately estimate the output values. If, for example, the difference in temperatures is quantitatively 0.5 degrees, then it is foolish to measure it with a room thermometer, with an error of 2 degrees. It is worth mentioning that the Newton-Richman law is valid only if the heat in the water spreads much easier than through the walls of the glass. In addition, the thermal conductivity, as well as the specific heat capacity, may depend on temperature. Well, our conclusions for the cylindrical glass, and other geometry will make its own adjustments.

Heating and cooling
Heating and cooling obey the Newton-Richman law , the solution of which has the form:

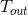 - ambient temperature;
- ambient temperature; - initial temperature;
- initial temperature; - time;
- time; - coefficient described below;
- coefficient described below;Let's explore this formula in detail:
')
- at the moment of time
 the temperature is equal to the initial
the temperature is equal to the initial  .Read more
.Read more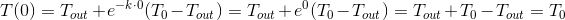
- over time, it tends to be environmental (no matter whether the initial was above or below it) exponentially, at a rate proportional to the coefficient
 .More detailsBecause
.More detailsBecause then
then 
Now a few words about the coefficient
 :
:
 - heat transfer coefficient, depending on many factors, obtained experimentally.
- heat transfer coefficient, depending on many factors, obtained experimentally. - the area of the interface;
- the area of the interface;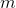 - weight;
- weight; - body specific heat;
- body specific heat;If with
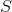 (contact area of water and vessel walls), specific heat capacity
(contact area of water and vessel walls), specific heat capacity  and mass
and mass 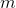 everything is clear, then with the heat transfer coefficient
everything is clear, then with the heat transfer coefficient  everything is not so obvious. It shows how many joules per second will go through the square meter boundary, with a temperature difference of 1 Kelvin. Fortunately, in our case, knowing the absolute value of this coefficient is not important.
everything is not so obvious. It shows how many joules per second will go through the square meter boundary, with a temperature difference of 1 Kelvin. Fortunately, in our case, knowing the absolute value of this coefficient is not important.Mixing
What will be the final temperature of the water after mixing? However trite it may sound, but for our case (we mix equal amounts of water):

 - temperature of hot (Hot) water;
- temperature of hot (Hot) water; - temperature of cold (Cold) water;
- temperature of cold (Cold) water; - mixture temperature;
- mixture temperature;Evidence
The amount of energy released or absorbed by the system, with a change in its temperature, is related by a simple relation:
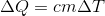
Hot water, cooling to will give the same amount of energy as the cold one takes, heating to the same temperature. Therefore, we can write:
will give the same amount of energy as the cold one takes, heating to the same temperature. Therefore, we can write:
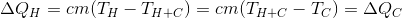


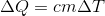
Hot water, cooling to
 will give the same amount of energy as the cold one takes, heating to the same temperature. Therefore, we can write:
will give the same amount of energy as the cold one takes, heating to the same temperature. Therefore, we can write: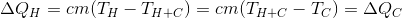


Glasses 2 and 4
The temperature of these glasses varies exponentially and over time
 will be:
will be: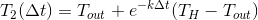

Next, mix and get:


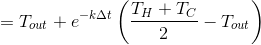
Glasses 1 and 3
We mix:

And through
 we get:
we get:
It would seem that there is no difference, but ...
Dirty trick or more about the k coefficient
From the point of view of heat loss, our cylindrical glass can be divided into three zones: the bottom (bottom), the upper part (top) and the side walls (sidewall). Therefore, the coefficient
 can be written as an amount:
can be written as an amount: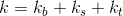
 ,
,  ,
, 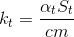
If the glass is considered as a cylinder with a radius
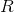 and tall
and tall  , then:
, then:

We can write:

So, for case 1 and 3, when mixed, the mass and height of the water column doubles:

But this has nothing to do with case 2 and 4, since they cool down (heat up) alone, and after mixing, a further change in temperature does not bother us at all.
Conclusions and another trick
If we consider


it can be concluded that
 will always be less than
will always be less than 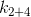 and therefore, if we recall that the coefficient determines the rate of temperature change, it is, in case of 1 and 3, less.
and therefore, if we recall that the coefficient determines the rate of temperature change, it is, in case of 1 and 3, less.The catch is the meaning
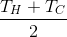 relative to ambient temperature. If this value is higher, then the cooling of the 1 + 3 mixture will be slower than 2 + 4 and, as a result, the temperature of the first will be higher. However, if you adjust the experiment in such a way that the average temperature is lower than the ambient temperature, the 2 + 4 mixture will be “hotter”, since it heats up faster.
relative to ambient temperature. If this value is higher, then the cooling of the 1 + 3 mixture will be slower than 2 + 4 and, as a result, the temperature of the first will be higher. However, if you adjust the experiment in such a way that the average temperature is lower than the ambient temperature, the 2 + 4 mixture will be “hotter”, since it heats up faster.Interesting
If you carefully consider the coefficients, you can make another interesting conclusion.
If we substitute this value in the formula for the final temperature for 1 + 3, we get:

Recall that

If to designate:
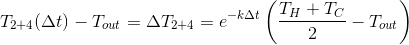
and
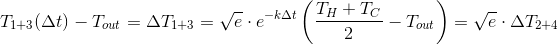
Thus, for an arbitrary cylindrical cup and ,
,  will lie between
will lie between  and
and  :
:

- If the cylinder is chosen in such a way that the ratio
 will be large enough (thin but long) so that
will be large enough (thin but long) so that 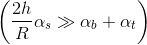 then
then  and their final temperatures will be almost the same.
and their final temperatures will be almost the same. - On the contrary, if the ratio
 small enough (wide but short) so that
small enough (wide but short) so that  then
then  .Read more
.Read more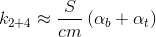

If we substitute this value in the formula for the final temperature for 1 + 3, we get:

Recall that

If to designate:
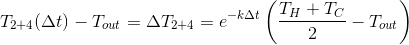
and
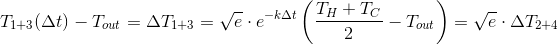
Thus, for an arbitrary cylindrical cup and
 ,
,  will lie between
will lie between  and
and  :
:
And in fact..?
In fact, this article is a very clear example of the fact that it is impossible to approach practice without a theory. And this paragraph contains conclusions more importantly than the above. Not knowing the fact that the result depends, among other things, on the ambient temperature, will lead to misinterpretation of the latter. Just imagine, two friends set up an experiment, cold water 5 degrees, hot 60. But one of them is at home 25, and the other 40. The results will be inconsistent. And if they also have different glasses or actions are not synchronous ... But much worse, it is false to say about the only correct outcome of the experiment, if the results are the same (due to the fact that hot water is more often "hotter" than cold "cooler" relative to room temperature ). Also, you should always at least approximately estimate the output values. If, for example, the difference in temperatures is quantitatively 0.5 degrees, then it is foolish to measure it with a room thermometer, with an error of 2 degrees. It is worth mentioning that the Newton-Richman law is valid only if the heat in the water spreads much easier than through the walls of the glass. In addition, the thermal conductivity, as well as the specific heat capacity, may depend on temperature. Well, our conclusions for the cylindrical glass, and other geometry will make its own adjustments.
Source: https://habr.com/ru/post/365325/
All Articles