Mathematical knitting

After dividing Habr into two resources, it turned out, I think not only for me, so that the articles remained on Habré, and only comments and rating were transferred to Hiktimes profile. At the same time, as a user without publications, I do not have the right to vote for the rating of the author's favorite articles, which I would like to correct. Ideas for articles if they were, then related to the subject of Habr. But the comment in the article “Two weeks after the appearance of Geektimes: alas ...” prompted a strange thought - to write about mathematical knitting. That is, about the various mathematical models, crocheted or knitting. Well, a little about the models themselves, too.

Strange attractor

Attractor (eng. Attract - attract, attract) is a compact subset of the phase space of a dynamic system, all trajectories from a certain neighborhood of which tend to it at a time tending to infinity. One of the nominal examples of the attractor is the Lorenz attractor.

The Lorenz attractor was found in Lorentz’s numerical experiments, which investigated the behavior of the trajectories of a nonlinear system:
')


with the values ​​of the parameters: σ = 10, r = 28, b = 8/3. The system arises in the following physical questions and models: convection in a closed loop, rotation of the water wheel, single-mode laser model, dissipative harmonic oscillator. The Lorentz model is a real physical example of dynamical systems with chaotic behavior.



The mathematician Hinke Osinga has a completely mathematical hobby - knitting. Counting loops in her free time, she rests. Once her supervisor, Professor Krauskopf imprudently quit: "Would you have connected something useful!" And Dr. Osinga tied up.

So the model of chaos appeared. Now the world's only knitted chaos is spinning under the ceiling in the office of mathematicians at the University of Bristol.

Hinke Osinga, Ph.D. in Mathematics, University of Bristol: “I was knitting every free minute. Mostly in the evenings. Approximately 2 hours a day for almost two months. A total of 85 hours. More than 25 thousand loops and chaos. And, very nice. " Now that you can touch it, it is easier for mathematicians to study it. They have been doing this for 2 years now (interview of 2004), modeling on a computer the “Lorentz equations”, which describe chaotic movements. Mathematicians promised a bottle of champagne to the first to offer another related model. Only two weeks later came the first letters with photos.

Hyperbolic plane

Lobachevsky geometry (hyperbolic geometry) is one of the non-Euclidean geometries, a geometric theory based on the same basic assumptions as ordinary Euclidean geometry, with the exception of the parallel axiom, which is replaced by the parallel Lobachevsky axiom. In Lobachevsky's geometry, the following axiom is assumed: at least two straight lines pass through a point that is not lying on a given straight line, lying with this straight line in the same plane and not intersecting it.

A pseudosphere (Beltrami surface) is a surface of constant negative curvature, formed by rotating the tractress near its asymptote. The name emphasizes the similarities and differences with the sphere, which is an example of a surface with a curvature, also constant, but positive. The name "pseudosphere" surface gave Beltrami.

He also drew attention to the fact that the pseudosphere implements a local model of Lobachevsky geometry.



Dayna Taimina solved the hundred-year problem of non-Euclidean geometry by visualizing hyperbolic planes. Hyperbolic planes are related to non-Euclidean geometry, which is traditionally difficult to visualize. Dayne Taimine managed to do it using knitted fabrics. She crocheted her first model of the hyperbolic plane in 1997 to use non-Euclidean geometry in the studio course. Since then, she has linked more than a hundred geometric patterns.





Its technique is used in ecology. Margaret Wertheim heads the project to recreate the inhabitants of the coral reef, using the crochet technique (crochet), invented by the mathematician - glorifying the awesomeness of the coral reef, and plunging into the hyperbolic geometry that underlies the creation of coral.
TED video: Margaret Wertheym on beautiful coral mathematics (and crochet knitting) , where a simple explanation of Euclidean and hyperbolic space is given.

Bottle of klein

The Klein bottle is a non-orientable (one-sided) surface, first described in 1882 by the German mathematician F. Klein. It is closely related to the Mobius band and the projective plane. The name, apparently, comes from the incorrect translation of the German word Fläche (surface), which in German is close in spelling to the word Flasche (bottle); then this name returned to German in this form.

The Klein surface in the form of “figure 8” shown in the figure below can be represented as a system of equations with parameters that looks much simpler than for the classic Klein bottle:







If you cut the Klein bottle into two halves along the plane of symmetry, you will get two Mobius' mirror ribbons, one with a half turn to the right, the other with a half turn to the left. In fact, it is possible to cut the Klein bottle so that you get one Moebius tape. Otherwise, the Klein bottle can be represented in the form of two Mobius tapes connected to each other by a conventional double-sided tape. In the figure below, the inner surface of this tape is painted white and the outer surface is blue.



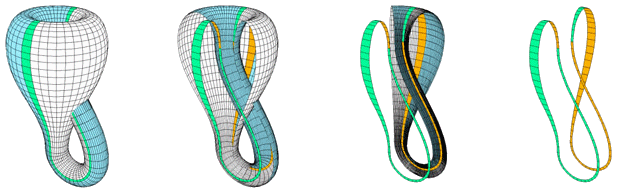
Klein Knitted Bottle:



As you can see, Acme also makes glass bottles.

Fractals

A fractal (latin. Fractus - crushed, broken, broken) is a mathematical set that has the property of self-similarity, that is, homogeneity in different scales of measurement (any part of the fractal is similar to the whole set). In mathematics, fractals are understood to mean sets of points in Euclidean space that have a fractional metric dimension (in the sense of Minkowski or Hausdorff), or a metric dimension that is different from the topological one, so they should be distinguished from other geometric shapes bounded by a finite number of links.

Beginning in the late 19th century, examples of self-similar objects with properties that are pathological from the point of view of classical analysis appear in mathematics. The Sierpinski triangle is a fractal, one of the two-dimensional analogues of the Cantor set, proposed by the Polish mathematician Václav Sierpinski in 1915. Also known as the “lattice” or “napkin” of Sierpinski. The midpoints of the sides of an equilateral triangle T0 are connected by segments. 4 new triangles are obtained. The interior of the middle triangle is removed from the original triangle. It turns out the set T1 consisting of 3 remaining triangles of the “first rank”. Doing exactly the same with each of the triangles of the first rank, we obtain the set T2, consisting of 9 equilateral triangles of the second rank. Continuing this process infinitely, we obtain an infinite sequence T0⊃T1⊃ ⋯ ⊃Tn⊃ ..., the intersection of whose members is the Sierpinski triangle.



Dr. David Wilstrom though a man, but also sometimes knits. Knitting was taught at one of the textile workshops, and since then he has been doing interesting things from threads in his free time.



And finally, some more knitted fractals.

Pythagorean tree



These rugs were created by the company Woolly Thoughts. They also make unusual panels , the image on which is visible only at a certain angle.

A lot of Julia

Sources:

About knitted attractor
Hinke Osing and Bernd Krauskopf website
Hyperbolic knitting
Dayna Tyminya
Hyperbolic Crochet
About Daina Taimini Exhibition
Bottle of klein
Acme klein bottle company
Mathematical Knitting Network
Pythagorean tree
An article about math knitting, but images are not available.