Thirty-six degrees of beauty
Grid systems of coordinates, in which the plane is divided into identical symmetric elements - into squares, triangles, hexagons, are well known. They correspond to square, triangular, hexagonal symmetry. But there is still a decagonal symmetry.
In it, the plane is not divided into decagons; instead, all the lines are located at angles of multiples of 36 °. Coordinates in this system can be written with integers, two integers each in the horizontal and vertical direction.

')
I'll tell you how to draw it.
The number of unit vectors in all directions in this frame of reference is ten. If we consider the symmetry of the opposite direction, then five. If we consider the horizontal symmetry, then three. Let's designate them as and output analytical expressions for them.
The usual formula for calculating coordinates when turning:
Double angle with this formula:
Means
And based on the fact that there is a difference in coordinates
Get the quadratic equation
Which is solved
This suggests that there is both a positive and a negative coordinate value. at which the difference of the coordinates of the double and single angle same.
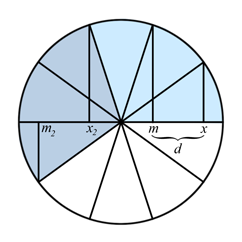
A decagon has such symmetry that the difference in the horizontal coordinate between a single and a double angle when the angles are increased three times, that is, between a triple angle and a sixfold one, retains exactly the same value. The absolute values of the coordinates m and x in the pair solution change places and change their sign, leaving the value of the difference the same. So, we can associate the second solution of a quadratic equation with a triple angle.
Using that
Will get
And immediately get the other values.
Number This is a small coefficient of the golden section.
Number This is a big golden ratio.
Their main properties are:
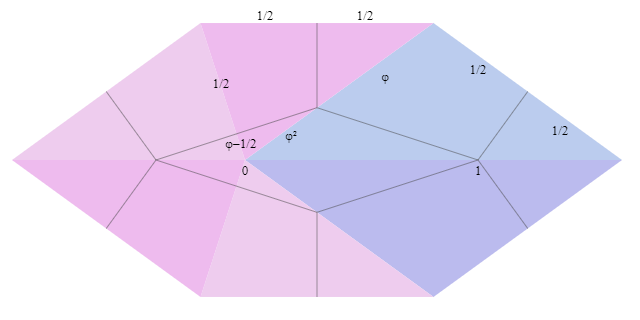
The coordinate system in which the coordinates are integers, and you can make turns at 36 ° is defined as:
Used constants are equal
This allows us to present three basic vectors. as

When combining unit vectors, the group parity of coordinates is preserved, and there can be only one of the following types:
.
That is, restrictions are imposed on the coordinates
Where - whole numbers.
Transforming the multiplication table
You can get an integer three-dimensional matrix for multiplying vectors.
Using this coordinate system, we position the points with perfect precision of integers.
A little more theory about the relationship of numbers: the degree of the number of phi and Fibonacci sequence.
With all the similarities formulas
they certainly vary.
Function this is a power function that is strictly greater than zero. And in the Fibonacci sequence there is a zero, and because of this, all the numbers preceding it alternate the sign.
To solve the equation fits not only , but also . Moreover, they are suitable at the same time. . If a and , the coefficients .
So, there is a formula that links the Fibonacci sequence and the power function of the number of phi (Binet formula):
For numbers with positive numbers, the value is predominantly set to the left term, and the right one aligns to an integer. For numbers with a negative number, the main contribution comes from the right term.
Inverse Formula from the fibonacci sequence:
For the number which in high degrees approaches zero, the difference in sign of numbers with negative numbers and the approximate equality of the ratio of neighboring numbers to the number itself are used. .
In the system of integer coordinates, this finds expression in the fact that base vectors with a multiplier
expressed in integer coefficients taken from the Fibonacci sequence:
These vectors can be divided.
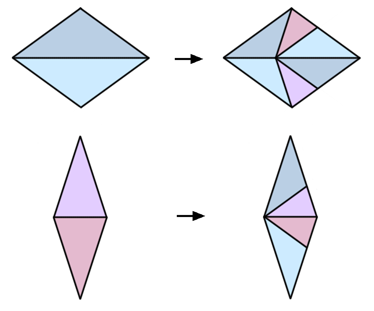
Now you can try to make triangles.
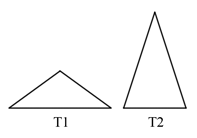
There are not so many triangles in which the angles are multiples of 36 °, just two. The sum of the angles in the triangle is 180 °, in parts the sum of the angles must be equal to five. How to divide 5 by three integers? The unit should be, because without it, even a minimum of three deuces is a bust. The remaining 4 lobes can be divided only as 1 + 3 and 2 + 2. Both triangles are isosceles and have a pair of identical angles.
Denote the triangles as T 1 and T 2 , according to size in fractions of the angle that is repeated.
Now you can try to break the triangles.
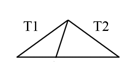
Triangle T 1 can be divided into two triangles: T 1 and T 2 .
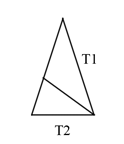
Triangle T 2 can be divided into two triangles: T 1 and T 2 .
Triangle T 1 can also be divided into three triangles: T 1 , T 2 , T 1 . Moreover, there are two such divisions: symmetric and antisymmetric.

These splits reduce the sides of the triangles by the same factor. .
From such triangles you can build a Penrose mosaic.
To build, you can proceed from the following rules:
1. For each level of partitioning, all triangles have the same length of the sides, and the base is connected to the same triangle, which is divided into a more detailed level symmetrically with the original one. It is because of this rule that Penrose mosaic can be represented by equilateral diamonds.
2. To split the triangle T 1 , only the asymmetric variant is used.
That is why Penrose mosaics can be represented by splitting into deltoids:
The resulting T 1 is sure to have a paired triangle that forms a corner with the source, the dart (dart). And the resulting T 2 pair triangle together with the neighboring form a convex deltoid “kite” (kite).

Although they themselves can be obtained by dividing a rhombus, deltoids in a mosaic are arranged so that they never merge into a rhombus. The complex form of deltoids has an advantage: a rhombus with one form can have two possible directions, while with the deltoids it is explicitly defined.
If we have connected triangles T 1 and T 2 , then the further construction has two options: either they together form T 2 and it means that at the general level it has its reflection. Either T 1 and T 2 together form part of the T 1 split, and then the continuation looks less symmetrical.

Therefore, it is more convenient to build a Penrozua mosaic not by building on the outside, but by dividing it inside.
Regarding division, triangles differ not only in shape, but also in the direction of symmetry. "Right" and "Left" triangles are cut in the opposite way. Therefore, we must immediately find out what type of triangles are obtained when dividing.
We will get the rules
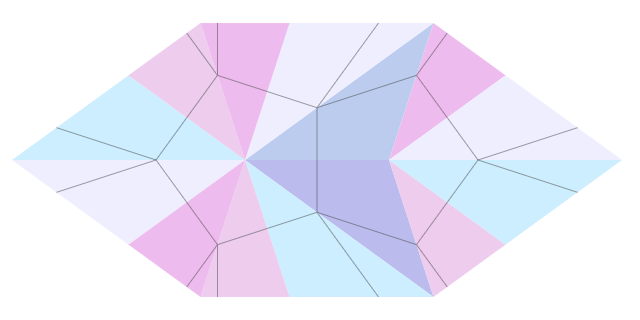
It turns out that rhombuses have four kinds of sides: those that are divided during splitting — with the shifted location of the splitting right or left, and those that do not divide, but form a diagonal for T 1 — either right or left. Knowing which sides fit together, it is possible to paint mosaic tiles so that the lines of the pattern dock at the borders, and then nice patterns are obtained.
The Penrose mosaic has several representations, but as a universal one, you can use the form of six triangles, four of which repeat the splitting shown from the triangles, and two additional, types T 1 , are similar in splitting to the first and second, but differ in that at the previous level of splitting Part T 1 of exactly the same type - left from left, right from right.

Such triangles can be combined into various types of mosaic: in diamonds, and in deltoids, and in triangles with different sides, and in HBS figures. And for the representation of P1, for the representation of straight lines and for a set of quadrangles, it is necessary to compare two basic triangles of the splitting line.
List of views:
To make a mosaic on a computer, just write a html page with javascript code in a text editor and open this page in a browser.
All text of the page without code:
We receive "context", the object interface for drawing on the plane:
The program will calculate the figures, and then draw them, depending on the settings specified.
Functions to simplify drawing commands:
The mosaic will consist of figures, they are stored as an array of data: the type of the figure, from 0 to 5, the coordinates of the anchor angle, the array of four integers, and the direction, 0 to 9. In the drawing function, the coordinate scale and step size for drawing the sides of the figure are set separately.
First, we define a basic shape of six triangles.
It remains to set the modes exactly how the figures can be displayed.
The code can be copied from the article to the file fragment by fragment and it will work.
Since each triangle has a paired triangle (except those on the border), for better drawing you can add a mode in which one of the pair of triangles is displayed with a diamond, and the second is not displayed. The same can be done with deltoids and with a triangle combined from two.
To split P1, you must specify two lines per triangle.


To represent a line mosaic, you need to define the following partition:
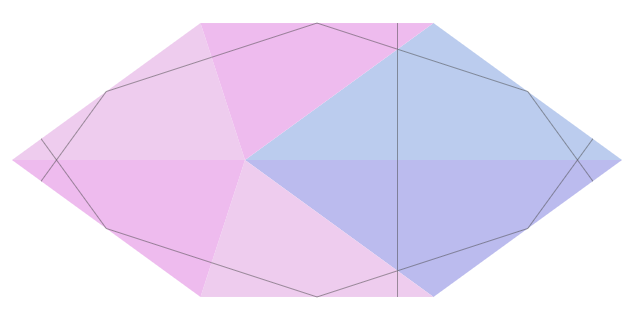
After three levels the lines repeat:

From this we can derive the coefficients of the proportions of the division of the line of the parties at the intersection. After shifting to three levels, the side of the triangle becomes . Solving the equation will get and the coefficient will be equal to .
The proportions of division are obtained:
- division of the side in the middle.
- division of a single diagonal.
- projection of the diagonal to the side.
- the first projection on the diagonal of a wide rhombus.
- the second projection on the diagonal of a wide rhombus.
- projection on the diagonal of a narrow rhombus
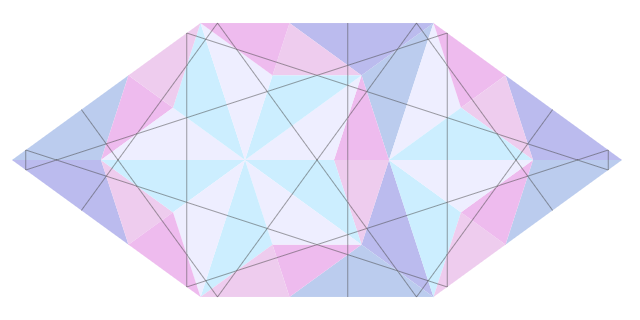
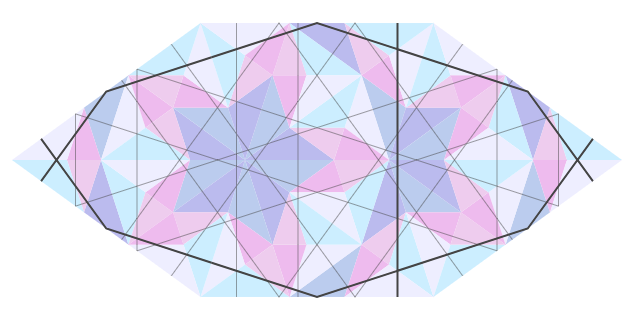
It turns out that the triangles at which the anchor angles coincide form HBS shapes. And to draw a partition on HBS, it suffices to display the far edge. If the triangles are scaled without changing the anchor, then around the figures empty space is formed. In this empty space, you can display the figures of the previous level by scaling them so that they touch the figures of this level. That is how the first image of the article is drawn.





To display a display of seven quadrilaterals, the base of each triangle and its height are drawn.

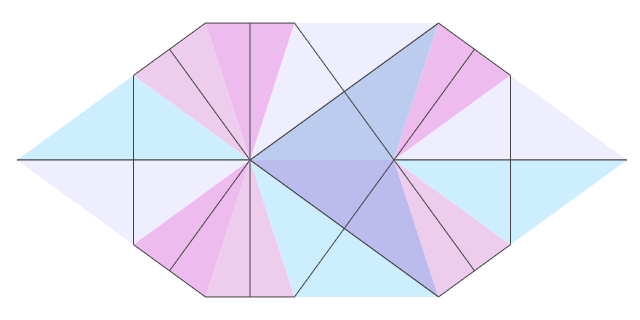


In my opinion, very beautiful.
In it, the plane is not divided into decagons; instead, all the lines are located at angles of multiples of 36 °. Coordinates in this system can be written with integers, two integers each in the horizontal and vertical direction.

')
I'll tell you how to draw it.
The number of unit vectors in all directions in this frame of reference is ten. If we consider the symmetry of the opposite direction, then five. If we consider the horizontal symmetry, then three. Let's designate them as and output analytical expressions for them.
The usual formula for calculating coordinates when turning:
Double angle with this formula:
Means
And based on the fact that there is a difference in coordinates
Get the quadratic equation
Which is solved
This suggests that there is both a positive and a negative coordinate value. at which the difference of the coordinates of the double and single angle same.

A decagon has such symmetry that the difference in the horizontal coordinate between a single and a double angle when the angles are increased three times, that is, between a triple angle and a sixfold one, retains exactly the same value. The absolute values of the coordinates m and x in the pair solution change places and change their sign, leaving the value of the difference the same. So, we can associate the second solution of a quadratic equation with a triple angle.
Using that
Will get
And immediately get the other values.
Number This is a small coefficient of the golden section.
Number This is a big golden ratio.
Their main properties are:
The coordinate system in which the coordinates are integers, and you can make turns at 36 ° is defined as:
Used constants are equal
This allows us to present three basic vectors. as

When combining unit vectors, the group parity of coordinates is preserved, and there can be only one of the following types:
.
That is, restrictions are imposed on the coordinates
Where - whole numbers.
Transforming the multiplication table
| * | one | φ | K 3 | K 2 |
|---|---|---|---|---|
| one | one | φ | K 3 | K 2 |
| φ | φ | 1-φ | K 2 | K 3 -K 2 |
| K 3 | K 3 | K 2 | 3 + φ | 1 + 2φ |
| K 2 | K 2 | K 3 -K 2 | 1 + 2φ | 2-φ |
Using this coordinate system, we position the points with perfect precision of integers.
A little more theory about the relationship of numbers: the degree of the number of phi and Fibonacci sequence.
With all the similarities formulas
they certainly vary.
Function this is a power function that is strictly greater than zero. And in the Fibonacci sequence there is a zero, and because of this, all the numbers preceding it alternate the sign.
To solve the equation fits not only , but also . Moreover, they are suitable at the same time. . If a and , the coefficients .
So, there is a formula that links the Fibonacci sequence and the power function of the number of phi (Binet formula):
For numbers with positive numbers, the value is predominantly set to the left term, and the right one aligns to an integer. For numbers with a negative number, the main contribution comes from the right term.
Inverse Formula from the fibonacci sequence:
For the number which in high degrees approaches zero, the difference in sign of numbers with negative numbers and the approximate equality of the ratio of neighboring numbers to the number itself are used. .
In the system of integer coordinates, this finds expression in the fact that base vectors with a multiplier
expressed in integer coefficients taken from the Fibonacci sequence:
These vectors can be divided.
Now you can try to make triangles.
There are not so many triangles in which the angles are multiples of 36 °, just two. The sum of the angles in the triangle is 180 °, in parts the sum of the angles must be equal to five. How to divide 5 by three integers? The unit should be, because without it, even a minimum of three deuces is a bust. The remaining 4 lobes can be divided only as 1 + 3 and 2 + 2. Both triangles are isosceles and have a pair of identical angles.
Denote the triangles as T 1 and T 2 , according to size in fractions of the angle that is repeated.

Now you can try to break the triangles.
Triangle T 1 can be divided into two triangles: T 1 and T 2 .

Triangle T 2 can be divided into two triangles: T 1 and T 2 .

Triangle T 1 can also be divided into three triangles: T 1 , T 2 , T 1 . Moreover, there are two such divisions: symmetric and antisymmetric.

These splits reduce the sides of the triangles by the same factor. .
From such triangles you can build a Penrose mosaic.
To build, you can proceed from the following rules:
1. For each level of partitioning, all triangles have the same length of the sides, and the base is connected to the same triangle, which is divided into a more detailed level symmetrically with the original one. It is because of this rule that Penrose mosaic can be represented by equilateral diamonds.
2. To split the triangle T 1 , only the asymmetric variant is used.
That is why Penrose mosaics can be represented by splitting into deltoids:
The resulting T 1 is sure to have a paired triangle that forms a corner with the source, the dart (dart). And the resulting T 2 pair triangle together with the neighboring form a convex deltoid “kite” (kite).

Although they themselves can be obtained by dividing a rhombus, deltoids in a mosaic are arranged so that they never merge into a rhombus. The complex form of deltoids has an advantage: a rhombus with one form can have two possible directions, while with the deltoids it is explicitly defined.
If we have connected triangles T 1 and T 2 , then the further construction has two options: either they together form T 2 and it means that at the general level it has its reflection. Either T 1 and T 2 together form part of the T 1 split, and then the continuation looks less symmetrical.

Therefore, it is more convenient to build a Penrozua mosaic not by building on the outside, but by dividing it inside.
Regarding division, triangles differ not only in shape, but also in the direction of symmetry. "Right" and "Left" triangles are cut in the opposite way. Therefore, we must immediately find out what type of triangles are obtained when dividing.
We will get the rules

It turns out that rhombuses have four kinds of sides: those that are divided during splitting — with the shifted location of the splitting right or left, and those that do not divide, but form a diagonal for T 1 — either right or left. Knowing which sides fit together, it is possible to paint mosaic tiles so that the lines of the pattern dock at the borders, and then nice patterns are obtained.
The Penrose mosaic has several representations, but as a universal one, you can use the form of six triangles, four of which repeat the splitting shown from the triangles, and two additional, types T 1 , are similar in splitting to the first and second, but differ in that at the previous level of splitting Part T 1 of exactly the same type - left from left, right from right.

Such triangles can be combined into various types of mosaic: in diamonds, and in deltoids, and in triangles with different sides, and in HBS figures. And for the representation of P1, for the representation of straight lines and for a set of quadrangles, it is necessary to compare two basic triangles of the splitting line.
Universal view

List of views:
- Of two triangles (four types) with the same sides

- From two triangles (four types) with different sides

- From a pair of rhombuses, representation P3

- From a diamond and a corner of two types

- Deltoid pair, P2 view: dart / kite

- P1 view: pentagons, star, boat, rhombus

- Presentation of "Hexagon, Boat, Star", HBS

- Special view: just intersecting straight lines

- Seven quadrangles (Seven kinds of quadrangles, the number of forms is only six)

To make a mosaic on a computer, just write a html page with javascript code in a text editor and open this page in a browser.
All text of the page without code:
<html><canvas id="a" width="640" height="320"></canvas><script> </script></html> We receive "context", the object interface for drawing on the plane:
var canvas = document.getElementById("a"); var b = canvas.getContext("2d"); The program will calculate the figures, and then draw them, depending on the settings specified.
Functions to simplify drawing commands:
// function begin(){b.beginPath();} // function from(p) {b.moveTo(s[8] + p[0], s[9] - p[1]);} // function to(p){b.lineTo(s[8] + p[0], s[9] - p[1]);} // , function close(){b.closePath();} // function fill(color){b.fillStyle = color; b.fill();} // function line(){b.strokeStyle = "#444"; b.lineWidth = 0.5; b.stroke();} function line_white(){b.strokeStyle = "#fff"; b.lineWidth = 1; b.stroke();} function line_black(){b.strokeStyle = "#444"; b.lineWidth = 1.5; b.stroke();} The mosaic will consist of figures, they are stored as an array of data: the type of the figure, from 0 to 5, the coordinates of the anchor angle, the array of four integers, and the direction, 0 to 9. In the drawing function, the coordinate scale and step size for drawing the sides of the figure are set separately.
First you need to set the used constants.
var s; function prepare() { var sqrt = Math.sqrt; var fi = (sqrt(5) - 1) / 2; var fb = (sqrt(5) + 1) / 2; var f3 = sqrt(3 + fi); var f2 = sqrt(2 - fi); // var vt = [[ 2, 0, 0, 0], [ 1, 1, 0, 1], [ 0, 1, 1, 0], [ 0,-1, 1, 0], [-1,-1, 0, 1], [-2, 0, 0, 0], [-1,-1, 0,-1], [ 0,-1,-1, 0], [ 0, 1,-1, 0], [ 1, 1, 0,-1]]; // var c = [1/2, fi/2, f3/2, f2/2] // // // . // // . var s = [0, vt, c, fi, f3, f2, 0, 0, 0, 0]; return s; } s = prepare(); s[0] = b; s[7] = 1; // s[8] = 500/2; // x s[9] = 320/2; // y First, we define a basic shape of six triangles.
First Level Fill Code
var f = []; // . f[0] = []; f[0].push([0,[ 0, 0, 0, 0],0]); f[0].push([1,[ 0, 0, 0, 0],0]); f[0].push([2,[ 0, 0, 0, 0],3]); f[0].push([3,[ 0, 0, 0, 0],3]); f[0].push([2,[ 0, 0, 0, 0],7]); f[0].push([3,[ 0, 0, 0, 0],7]); Code calculation and drawing levels
fi = s[3]; // var levels = 3; // s[7] = 0.1 * 10; // s[10] = 24 * 6 * fi * fi; // //s[10] = 24 * 6 * fi //s[10] = 24 * 6; // , , p[0] p[1] from() to(). //s[10] = 24; mode = 12; // // var n = 0, m; for(; n < levels; n++) { m = n + 1; f[m] = []; for(var k = 0; k < f[n].length; k++) zd(f[n][k], s, f[m]); } // n = m - 1; // if(s[7] != 1) for(var i = 0; i < f[n].length; i++) {paint(f[n][i], mode, 1);} // for(var i = 0; i < f[m].length; i++) {paint(f[m][i], mode, 0);} // 11 if(mode == 11) {d = 3; for(var i = 0; i < f[md].length; i++) {paint(f[md][i], mode, d);}} Split function
function zd(a, s, f) { var t = a[0]; // var vt = s[1]; // if (t > 3) t = t - 4; // 4 5 0 1 // , sht = [ 1,-1, 2,-2]; var shift = sht[t]; if(t == 0) {t1 = 0; t2 = 3; t3 = 5;} // else if(t == 1) {t1 = 1; t2 = 2; t3 = 4;} else if(t == 2) {t1 = 4; t2 = 2;} else if(t == 3) {t1 = 5; t2 = 3;} if (t < 2) { pos = a[1]; v1 = a[2]; // v2 = (v1 + shift + 10) % 10; // v3 = (v1 - shift + 10) % 10; // v4 = (v2 + 5) % 10; // v5 = (v1 + 5) % 10; // ( ) p1 = add(pos, vt[v2]); // p2 = add(p1, vt[v3]); // p3 = mul(p1,[2,2,0,0]); // p4 = mul(p2,[2,2,0,0]); // f.push([t1, p3, v4]); f.push([t2, p3, v3]); f.push([t3, p4, v5]); } else { pos = a[1]; v1 = a[2]; v2 = (v1 + shift + 10) % 10; // v3 = (v1 - shift + 10) % 10; // v4 = (v2 + 5) % 10; // v5 = (v3 + 5) % 10; // p1 = add(pos, vt[v2]); // p2 = add(p1, vt[v3]); // p3 = mul(p1,[2,2,0,0]); // p4 = mul(p2,[2,2,0,0]); // f.push([t1, p3, v4]); f.push([t2, p4, v5]); } return f; } Used functions of addition and multiplication of vectors
function mul(v1, v2) { mt = [[[1, 0, 0, 0],[0, 1, 0, 0],[ 0, 0, 1, 0],[ 0, 0, 0, 1]], [[0, 1, 0, 0],[1,-1, 0, 0],[ 0, 0, 0, 1],[ 0, 0, 1,-1]], [[0, 0, 1, 0],[0, 0, 0, 1],[-3, 1, 0, 0],[-1,-2, 0, 0]], [[0, 0, 0, 1],[0, 0, 1,-1],[-1,-2, 0, 0],[-2, 1, 0, 0]]] var v3 = [0, 0, 0, 0]; for(var i = 0; i < 4; i++) for(var j = 0; j < 4; j++) for(var k = 0; k < 4; k++) v3[k] = v3[k] + v1[i] * v2[j] * mt[i][j][k]; for(var i = 0; i < 4; i++) v3[i] = v3[i] / 2; return v3; } function add(v1, v2) { // , // . var v3 = [0, 0, 0, 0]; for(var i = 0; i < 4; i++) v3[i] = v3[i] + v1[i]; for(var i = 0; i < 4; i++) v3[i] = v3[i] + v2[i]; return v3; } The function of finding a point between two, with a given coefficient.
function mean(p1, p2, d) { var p3 = [(p2[0] - p1[0]) * d + p1[0],(p2[1] - p1[1]) * d + p1[1]]; return p3; } It remains to set the modes exactly how the figures can be displayed.
Shape drawing function
function paint(a, mode, level = 0) { vt = s[1]; // c = s[2]; // fi = s[3]; // pr = s[7]; // b = s[0]; // var st = s[10]; // colors = ["#BCE","#BBE","#ECE","#EBE","#CEF","#EEF"]; type = a[0]; // tn = type; // 4 if(tn > 3) tn = tn - 4; // color = colors[type]; // , sht = [ 1,-1, 2,-2]; var shift = sht[tn]; p = a[1]; // v0 = a[2]; // v0 = (10 + v0 % 10) % 10; // 0-10 v1 = (10 + (v0 + shift) % 10) % 10; // v2 = (10 + (v0 - shift) % 10) % 10; // // . var kop = 0; var koe = 0; pr1 = 1 - pr; // . if(level == 0) {kop = st; koe = pr;} if(level == 1) {kop = st / fi; koe = pr1 / fi; } // if(level == 3) {kop = st / fi / fi / fi; koe = pr / fi / fi / fi; } // st = st * koe; // . // p0 = [kop * (p[0] * c[0] + p[1] * c[1]), kop * (p[2] * c[2] + p[3] * c[3])] // s1 = vt[v1]; p1 = [p0[0] + st * (s1[0] * c[0] + s1[1] * c[1]), p0[1] + st * (s1[2] * c[2] + s1[3] * c[3])]; // s2 = vt[v2]; p2 = [p1[0] + st * (s2[0] * c[0] + s2[1] * c[1]), p1[1] + st * (s2[2] * c[2] + s2[3] * c[3])]; // modes = [1, 1,1,1,1,1, 0,0,0,0,1, 1,1,1]; y = modes[mode]; // , if(level < 3) // , , 11 . if(y || mode == 0) { begin(); from(p0); to(p1); to(p2); close(); if(y) {fill(color);} if(mode == 0) line(); if(mode == 12) line_white(); } // if(mode == 1) { p3 = mean(p0, p2, 0.5); begin(); from(p0); to(p2); from(p1); to(p3); line_black(); } // , HBS if(mode == 2) { begin(); from(p1); to(p2); line(); } if(mode == 6) // { begin(); if(tn == 0 || tn == 2) { color = colors[tn * 2]; // p3 = mean(p0, p2, 0.5); p4 = mean(p1, p3, 2); from(p0); to(p1); to(p2); to(p4); close(); fill(color); } line(); } if(mode == 7) // { if(type == 0) { // p3 = mean(p0, p1, 1 + fi); p4 = mean(p2, p3, 1 + fi); begin(); from(p0); to(p1); to(p4); to(p2); close(); fill(colors[0]); line(); } if(type == 2) { // p3 = mean(p0, p2, 2 + fi) p4 = [p0[0] + (p2[0] - p1[0]), p0[1] + (p2[1] - p1[1])]; begin(); from(p0); to(p1); to(p3); to(p4); close(); fill(colors[4]); line(); } } if(mode == 8) // { if(type < 2) { begin(); from(p0); to(p1); to(p2); close(); fill(colors[0]); line(); } if(type == 4 || type == 5) { p3 = mean(p0, p1, 1 + fi); begin(); from(p0); to(p3); to(p2); close(); fill(colors[4]); line(); } } if(mode == 9) // { if(type == 0) { p3 = mean(p0, p1, 1 + fi); p4 = mean(p2, p3, 1 + fi); begin(); from(p0); to(p1); to(p4); to(p2); close(); fill(colors[0]); line(); } if(type == 2) { p3 = [p0[0] - p1[0] + p2[0], p0[1] - p1[1] + p2[1]]; begin(); from(p0); to(p1); to(p2); to(p3); close(); fill(colors[4]); line(); } if(type == 4) { p3 = mean(p2, p1, 1 + fi); p4 = mean(p0, p3, 1 + fi); begin(); from(p0); to(p4); to(p1); to(p2); close(); fill(colors[0]); line(); } } if(mode == 10) { p4 = mean(p1, p0, fi); p5 = mean(p0, p2, fi); p6 = mean(p2, p0, 1 / 2 + fi / 2); p7 = mean(p1, p2, 0.5); begin(); if(tn < 2) {from(p4); to(p5);} else {from(p6); to(p4);} to(p7); line(); } if(mode == 11) { k1 = 1 / 2; k2 = (fi + 1) / 2; k3 = (4 - fi) / 4; k4 = (fi + 1) / 4; k5 = (3 - 2 * fi) / 2; k6 = 1 / 4; if(tn < 2) { p3 = mean(p0, p2, k4); p4 = mean(p0, p1, k2); p5 = mean(p1, p2, k1); p6 = mean(p0, p2, k5); p7 = mean(p1, p2, k3); begin(); from(p3); to(p4); to(p5); to(p6); to(p7); } else { p3 = mean(p2, p1, k3); p4 = mean(p0, p1, k2); p5 = mean(p1, p2, k1); p6 = mean(p2, p0, k6); begin(); from(p3); to(p4); to(p5); to(p6); } line(); } } The code can be copied from the article to the file fragment by fragment and it will work.
Since each triangle has a paired triangle (except those on the border), for better drawing you can add a mode in which one of the pair of triangles is displayed with a diamond, and the second is not displayed. The same can be done with deltoids and with a triangle combined from two.
To split P1, you must specify two lines per triangle.




To represent a line mosaic, you need to define the following partition:

After three levels the lines repeat:



From this we can derive the coefficients of the proportions of the division of the line of the parties at the intersection. After shifting to three levels, the side of the triangle becomes . Solving the equation will get and the coefficient will be equal to .
The proportions of division are obtained:
- division of the side in the middle.
- division of a single diagonal.
- projection of the diagonal to the side.
- the first projection on the diagonal of a wide rhombus.
- the second projection on the diagonal of a wide rhombus.
- projection on the diagonal of a narrow rhombus
It turns out that the triangles at which the anchor angles coincide form HBS shapes. And to draw a partition on HBS, it suffices to display the far edge. If the triangles are scaled without changing the anchor, then around the figures empty space is formed. In this empty space, you can display the figures of the previous level by scaling them so that they touch the figures of this level. That is how the first image of the article is drawn.





To display a display of seven quadrilaterals, the base of each triangle and its height are drawn.




In my opinion, very beautiful.
Source: https://habr.com/ru/post/359244/
All Articles