A bunch of different ways to read bits

Renewing the old tradition of my blog, I will take a simple task, consider an excessively long list of its alternative solutions and assess their merits.

Our simple task will be the following: we want to read data from a byte stream, values ​​encoded with a variable number of bits. Read individual bytes, machine words, etc. directly supported by most processors and many programming languages, but with variable-length input / output, it is usually necessary to implement the solution yourself.

It sounds simple enough, and in a sense it is. The first source of problems is that this operation will actively use codecs - and yes, it will be limited to calculations, and not memory and I / O. Therefore, we need not just a working, but also an effective implementation. And on the way, we will face many other difficulties: interactions with I / O buffering, processing the end of the buffer, deadlocks in bit shifts defined in C / C ++ and in different processor architectures, as well as other features of bit shifts.
')
This post will mainly focus on a variety of different ways to implement the reader; in fact, all the techniques considered here are similarly applicable to the recording part, but I do not want to double the number of variations of the algorithms. They will be enough.

Degrees of freedom

“Consider a variable number of bits” is an insufficient description of the task. There are many acceptable ways of packing bits into bytes, and all of them have their strengths and weaknesses, which I will discuss later. For now let's just dwell on their differences.

First we need to make the first important choice - the fields will be packaged as “first goes MSB” or “first goes LSB” (“most significant bit” is the most significant bit and “least significant bit” is the least significant bit). That is, if we call the implemented function getbits and execute the following code

 a = getbits(4); b = getbits(3); 

for the just-opened bitstream, we expect both values ​​to be received from the same byte, but how are they ordered in this byte? If packaged as MSB-first, then “a” occupies 4 bits, starting with MSB, and “b” is below “a”, which leads us to the following scheme:


I number the bits like this: LSB is 0 and approaching MSB, the values ​​increase. In many contexts, this order is standard. LSB-first is the opposite: the first field is bit 0, and the following fields contain increasing numbers of bits:


Both formats are used in common file formats. For example, JPEG uses bit packing in the bit stream in the MSB-first format, and DEFLATE (zip) uses LSB-first.

The next question we need to solve is what happens when the value is stretched a few bytes. Suppose we have one more “c” value that we want to encode in 5 bits. What we get as a result? We can slightly delay the solution of the problem by declaring that we are packing the values ​​into 32-bit or 64-bit words, not bytes, but in the end we have to choose something. And here we are suddenly faced with a variety of different options, so I will consider only the main applicants.

We can perceive the packing of MSB-first bits as an iteration over the “c” bit field from its MSB towards the LSB, with insertion one bit at a time. Filling one byte, we proceed to the next. If you follow these rules for our bit field c, then the result in our stream bits will be in the following scheme:


Keep in mind that following these rules, we end up with the same two bytes that we would get by wrapping the MSB bits into a large integer and storing it in big-endian order. If we instead decided to break the “c” in such a way that its LSB is in the first byte, and its four bits of a higher order are in the second byte, it would not work. I will call such consistent rules for packing bits "natural" rules.

Of course, the LSB-first bit packing has its own natural rule. It consists in inserting a new value bit by bit, starting from LSB and up, and if we do that, we will get the following bit stream as a result:


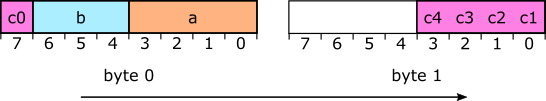
The LSB-first natural package gives us the same bytes as the LSB-first package in a large integer, saving it in little-endian byte order. In addition, we have obvious clumsiness in the figure: the logical conjugate packing of the “c” field in several bytes looks interrupted on this picture, while the MSB-first packing pattern looks as we expected. But the problem also arises in it: in the MSB-first pattern, we number the bits in the increasing order from right to left (standard), and the bytes in the order increasing from left to right (which is also standard).

This is what happens with the LSB-first bit scheme if we draw bit 0 (LSB) in each byte to the left , and bit 7 (MSB) to the right:


If we draw it like this, the scheme will look like the way we expected. The location of the MSB on the right seems strange if you think of a byte as a number, but it turns out to be much less strange if you think of it as an array of 8 bits (as we, in fact, work with it when performing bitwise I / O).

Coincidentally, in some big-endian architectures (for example, in IBM POWER), the bits are numbered as follows — bit 0 is MSB, bit 31 (or 63) is LSB. By creating an MSB-first bit packing scheme on such a machine with a bit of 0 = MSB, and numbering our own bit fields so that their bit 0 matches the MSB, we get exactly the same scheme (but this will mean that something is slightly different ). This standard makes the order of bits and bytes consistent (which is good), but destroys the convenient standard of matching the k bit to 2 ^k (which is not exactly good).

And if the idea of ​​renumbering bits in such a way that bit 0 is MSB explodes your brain, you can leave the numbering of bits unchanged, but become a rebel and draw the byte addresses increasing on the left. Or increase the address to the right, but become a slightly different rebel and write the byte stream in reverse order. If you choose one of these options, we get the following scheme:


I understand that this is already beginning to confuse, and I’ll stop at this, but here it’s necessary to say something important: you shouldn’t become too attached to the method of getting bytes. It is easy to be deceived when deciding that one option is better than another simply because it looks better, but the standards for getting the bytes from left to right and the bits inside them from right to left are completely arbitrary, so whatever you choose, you end up with something strange.

It turns out that each of the MSB-first and LSB-first packaging standards has its advantages and disadvantages, and it would be much more useful to think of them as tools with different application areas, rather than designating one of them as “right” and others as “wrong”. Regarding the byte order and the need to pack values ​​into bytes, words or something larger, I highly recommend you use the most natural order for your bit packing standard: MSB-first naturally corresponds to big-endian byte order, and LSB -first naturally corresponds to little-endian byte order. Unless you are writing byte streams in the reverse order (believe it or not, there are logical reasons for doing this); in this case, we get MSB-first in reverse order, corresponding to little-endian, and LSB-first in reverse order, corresponding to big-endian.

The reason for choosing the “natural” order is that they give us more freedom in different implementations. A stream with a natural order allows the use of many different decoders (and coders), each of which has its own trade-offs (and its own advantages in different cases). “Unnatural” orders are usually applied with one particular implementation and, when decoded in any other way, prove to be very inconvenient.

Our first getbits (bit extraction)

Now that we have sufficiently described the problem, we can implement a solution. A particularly simple version is possible if we assume that the entire bitstream is located in memory sequentially (as an array of bytes), and so far completely ignore the unpleasant problems like hitting the end of the array. Let's just pretend that it is infinite! (Either huge enough or has zero filling around the edges.)

In this case, we can base the implementation on a purely functional “bit extraction” function, in which I will illustrate the problems that arise and all the various bit-reading functions. Let's start by packing the LSB-first bits:

 //  buf[]    integer little-endian,  "width" // ,     "pos" (LSB= 0). uint64_t bit_extract_lsb(const uint8_t *buf, size_t pos, int width) { assert(width >= 0 && width <= 64 - 7); //  64-  little-endian,   , //    "pos" ( "buf"). uint64_t bits = read64LE(&buf[pos / 8]); //     ,  //   . //   LSB     LSB . bits >>= pos % 8; //   "width" ,      . return bits & ((1ull << width) - 1); } //  ,    //  - . const uint8_t *bitstream; //    size_t bit_pos; //      . uint64_t getbits_extract_lsb(int width) { //   uint64_t result = bit_extract_lsb(bitstream, bit_pos, width); //   bit_pos += width; return result; } 

We simply took advantage of the fact mentioned above that the LSB-first bit stream is just a big number little-endian. First we get 64 contiguous bits arranged in bytes, starting with the first byte containing any of the bits we are interested in, right shift to get rid of the remaining 0-7 extra bits below the first bit we need, and then return the result masked to the desired width.

Depending on the value of pos , this shift to the right can cost us an additional 7 bits. Therefore, although we read the full 64 bits, the maximum amount that we can read at one time using this code is 64-7 = 57 bits.

With bitextract , we can easily implement getbits ; we simply track the current position of the bitstream (in bits), and execute its increment after reading.

The corresponding option for MSB-first is quite similar, with the exception of one annoying problem, which I will discuss after demonstrating the code:

 //  buf[]    integer big-endian,  "width" // ,     "pos" (MSB= 0). uint64_t bit_extract_msb(const uint8_t *buf, size_t pos, int width) { assert(width >= 1 && width <= 64 - 7); //  64-  big-endian,   , //    "pos" ( "buf"). uint64_t bits = read64BE(&buf[pos / 8]); //     ,    . //   MSB      MSB . bits <<= pos % 8; //   "width" . return bits >> (64 - width); } uint64_t getbits_extract_msb(int width) { //   uint64_t result = bit_extract_msb(bitstream, bit_pos, width); //   bit_pos += width; return result; } 

This code works similarly to the previous one: we read 64 contiguous bits arranged in bytes (this time big-endian), we shift left to even the top of the bit field we need with MSB bits (while earlier we did right shift to align bottom of our bit field with LSB bits ), and then make a shift to the right to position the top width bits below to return them, because when we call getbits(3) we usually expect to see a value from 0 to 7.

Boundary cases of shifts

So what's the problem? This version of the code does not allow the width be zero. The problem is that if we allow width == 0 to be done, then the final shift will try to shift the 64-bit value to 64 bits to the right, and in C / C ++ this is undefined behavior! In this case, we can perform a shift of 0-63 bytes.

In some cases, C / C ++ leaves details undefined for backward compatibility with machines, so no one cares about that right now. A well-known example: the absence of the requirement that the representation of signed numbers use an additional code; Although there are architectures without additional code, all of them today are preserved only in museums.

Unfortunately, we have not one of these cases. This is what happens on various widely used CPU architectures when the amount of shift is outside the range:

• For 32-bit x86 and x86-64, the shift values ​​are interpreted as mod 32 for operand widths of 32 bits and lower, and mod 64 for 64-bit operands. That is, a shift to the right of a 64-bit value by 64 will result in the same as a shift by 0, i.e. no operation (no-op).
• In 32-bit ARM (A32 / T32 instruction sets), the shift value is taken mod 256. A right shift of a 32-bit value by 32 (or 64) will result in 0, as well as a right shift by 255, but a right shift by 256 will leave the value intact .
• In 64-bit ARM (A64 ISA), mod 32 for 32-bit shifts and mod 64 for 64-bit shifts are taken (essentially as in x86-64).
• RISC-V also follows the same rule: distances of 32-bit shifts are taken as mod 32, distances of 64-bit shifts - as mod 64.
• In POWER / PowerPC, 32-bit shifts take the mod 64 shift value, and 64-bit shifts take the mod 128 shift value.

To confuse us even more, most of these instruction sets have SIMD extensions, and integer SIMD instructions have a different behavior when shifting outside the interval, different from non-SIMD instructions. In short, this is one of those times when there are architectural differences between popular platforms; For most of you, POWER and RISC-V may seem a bit outdated, but, say, 32-bit and 64-bit ARMs are currently installed on hundreds of millions of devices.

Consequently, even if everything that the compiler does with this shift to the right - it gives the corresponding shift instruction to the right for the target architecture (and usually it does), then we will see different behavior on different architectures. On ARM A64 and x86-64, the shift result by 64 is essentially no-op, and getbits(0) will therefore (usually) return a non-zero value, although you should expect zero to return.

Why is this so important? Of course, the getbits(0) in the code is not an interesting use case; however, sometimes we need to getbits(x) for some variable x, where x in some cases can be zero. In this case, it would be great if the code just worked and did not require any special checks.

If you want this case to work, then one option is to explicitly check for width == 0 and handle this in a special way; Another option would be to use a non-branching expression that works with zero widths, for example, this code used in FSE Jenna Collet :

  //   "width" ,     width==0. return (bits >> 1) >> (63 - width); 

This particular case is easier to handle for LSB-first bitstreams. And since I mentioned them, let's talk about the operation of using a mask, which I applied to isolate the lower width bits:

  //   "width" ,      . return bits & ((1ull << width) - 1); 

There is a similar form that is slightly less expensive in architectures with a three-instruction and-with-complement (AND-NOT) instruction. These include many RISC CPUs, as well as x86s with BMI1 . Namely, we can take a mask of all bits-units, shift left to add width zeros to the bottom, and then add everything:

  return bits & ~(~0ull << width); 

If you have x86 not only with BMI1, but also with BMI2 support, you can also use the BZHI instruction, specially created for this case, if you figure out how to get the compiler to give it (or use an assembler). Another option that in some cases would be preferable is to simply prepare a small bitmask lookup table, which simplifies the code to this:

  return bits & width_to_mask_table[width]; 

Preparing a lookup table storing the result of two integer operations may seem like a ridiculous action, especially because calculating the address of the loaded table element usually involves both shifting and adding — exactly the same operations that we would have done if we hadn't tables! - but there is a method in this madness: the calculation of the required address can be performed as part of the memory access in one load instruction, for example, on machines with x86 and ARM, therefore these shift and addition are calculated in the Address Generation Unit (AGU) as part of the loading pipeline in the CPU, and not with instructions for integer arithmetic and shift. That is, such a counterintuitive solution of replacing two integer ALU instructions with a single instruction of loading an integer can lead to a significant acceleration of code with active bit I / O, because it balances the load between different operating units better.

Another interesting property is that the LSB-first version using the mask lookup table performs one shift by a variable (to shift the bits already read). This is important, because for many (often trivial!) Reasons, in many micro-architectures, shifts of integers by variables are more costly than shifts by constant values ​​of compile time. For example, Cell PPU / Xbox 360 Xenon was notorious for having shifted by a variable distance, slowing down the processor core for a terribly long time - 12 cycles, and the usual shifts were built into the pipeline and performed in two cycles. On many Intel x86 microarchitectures, “traditional” x86 shifts ( SHR reg, cl and the like) are three times more expensive than shifts by the compile time constant.

It seems that this is another reason for rejecting the MSB-first option: the above options perform two or three shifts per bit extraction operation, two of which have a variable distance. But there is a trick by which you can return to a single shift operation, namely using a cyclic instead of the usual shift:

 //  buf[]    integer big-endian,  "width" // ,     "pos" (MSB= 0). uint64_t bit_extract_rot(const uint8_t *buf, size_t pos, int width) { assert(width >= 0 && width <= 64 - 7); //  64-  big-endian,   , //    "pos" ( "buf"). uint64_t bits = read64BE(&buf[pos >> 3]); //   ,        LSB. bits = rotate_left64(bits, (pos & 7) + width); //   "width" . // (   ,       //      - LSB-first.) return bits & width_to_mask_table[width]; } 

Here, turning left (you have to figure out for yourself how best to use it in your C compiler) first performs the work of the original left shift, and then turns to additional “width” bits to make the bit field roll from the most significant bits of the value to the least significant , , LSB-first.

, , 8 3, mod-8 AND 7. , , .

( RAD Game Tools) Cell PPU Xbox 360, , . , width == 0 ; — , ( ) , C.

, . -: — , , , , , , !

, , . « » , , .

, , ( ). getbits - . .

1:

-«» , . ; , , , .

, . , « »:

 //        //  ,    . uint64_t bitbuf = 0; //     int bitcount = 0; //     

, , .

getbits , , MSB-first:

 // :  "bitbuf"  "bitcount" ,   // MSB  ;    "bitbuf" -  0. uint64_t getbits1_msb(int count) { assert(count >= 1 && count <= 57); //    ,       // Big endian;      , //    . while (bitcount < count) { bitbuf |= (uint64_t)getbyte() << (56 - bitcount); bitcount += 8; } //      ;   // "count"   "bitbuf"   . uint64_t result = bitbuf >> (64 - count); //       bitbuf <<= count; bitcount -= count; return result; } 

, count ≥1, , . ; , , - , .

: , . , , . , getbyte() - , ; , - . 8 , 57 ; , , .

count , . , MSB .

, , «» (refill), «» (peek) «» (consume). «» , ; «» , , «» , . ; , , LSB-first, :

 // :  "bitbuf"  "bitcount" ,   // LSB   ;    "bitbuf" -  0. void refill1_lsb(int count) { assert(count >= 0 && count <= 57); //      . while (bitcount < count) { bitbuf |= (uint64_t)getbyte() << bitcount; bitcount += 8; } } uint64_t peekbits1_lsb(int count) { assert(bit_count >= count); return bitbuf & ((1ull << count) - 1); } void consume1_lsb(int count) { assert(bit_count >= count); bitbuf >>= count; bitcount -= count; } uint64_t getbits1_lsb(int count) { refill1_lsb(count); uint64_t result = peekbits1_lsb(count); consume1_lsb(count); return result; } 

getbits . , MSB-first, , peekbits consume ; . , , - .

— . : , , :

  a = getbits(4); b = getbits(3); c = getbits(5); 

getbits , , ( ) . ; , 4+3+5=12 , :

  refill(4+3+5); a = getbits_no_refill(4); b = getbits_no_refill(3); c = getbits_no_refill(5); 

getbits_no_refill — getbits, peekbits consume , , , . getbits , , . , ; , , , , :

  temp = getbits(5); if (temp < 28) result = temp; else result = 28 + (temp - 28)*16 + getbits(4); 

, 0 27 5 , 28 91 9 . , , . , 9 , , :

  refill(9); temp = getbits_no_refill(5); if (temp < 28) result = temp; else result = 28 + (temp - 28)*16 + getbits_no_refill(4); 

, , , ( consume ) . , MSB-first, :

  refill(9); temp = peekbits(5); if (temp < 28) { result = temp; consume(5); } else { // ""  ""     , //      ! ! result = getbits_no_refill(9) - 28*16 + 28; } 

, , , . (, ) . , (.. ). , - ( , .)

. , , , : getbits . , 9 , 5 . , , .

lookahead . , . , , ; , . , ; .

, - . :

• - , , - . , .
• , , getbits , , ( - , ); , - ( ).
• , lookahead , , . , 64- , , - 8- (, - ). , , .
• , -, , , . , lookahead , , . , C ungetc , ungetc , . -.

— , : - — ; - — , - . , . , ; , , bitcount . , lookahead, - . , , .

2: 64

, . 64 , 7 , , getbits1 ; 57 , ( 65 , ), , getbits1 . 57 — , 32- , 25 (32-7), , .

, , ( MSB-first, RAD). , MSB-first LSB-first, . LSB-first:

 // : "bitbuf"  "bitcount" ,   // LSB  ; 1 <= bitcount <= 64 uint64_t bitbuf = 0; //     int bitcount = 0; //     uint64_t lookahead = 0; //  64  bool have_lookahead = false; //   ,   ! void initialize() { bitbuf = get_uint64LE(); bitcount = 64; have_lookahead = false; } void ensure_lookahead() { //   lookahead,  //     . if (!have_lookahead) { lookahead = get_uint64LE(); have_lookahead = true; } } uint64_t peekbits2_lsb(int count) { assert(bitcount >= 1); assert(count >= 0 && count <= 64); if (count <= bitcount) { //    buf return bitbuf & width_to_mask_table[count]; } else { ensure_lookahead(); //   bitbuf  lookahead // ( lookahead      buf) uint64_t next_bits = bitbuf; next_bits |= lookahead << bitcount; return next_bits & width_to_mask_table[count]; } } void consume2_lsb(int count) { assert(bitcount >= 1); assert(count >= 0 && count <= 64); if (count < bitcount) { // -   buf //    bitbuf >>= count; bitcount -= count; } else { //    buf  ensure_lookahead(); //      lookahead int lookahead_consumed = count - bitcount; bitbuf = lookahead >> lookahead_consumed; bitcount = 64 - lookahead_consumed; have_lookahead = false; } assert(bitcount >= 1); } uint64_t getbits2_lsb(int count) { uint64_t result = peekbits2_lsb(count); consume2_lsb(count); return result; } 

, , . , , , PC. , , width_to_mask_table , : , , 0-64 width 64- , IBM POWER. , , , , .

: . , 64- , peekbits , 64- ( get_uint64LE() ), , . , consume , width . , lookahead ( , ) have_lookahead , , lookahead .

, ( ). , , peekbits count <= bitcount , , consume count < bitcount . : next_bits peekbits bitcount . , bitcount < count ≤ 64, bitcount < 64 . consume : lookahead_consumed = count - bitcount . , , , lookahead_consumed ≥ 0; , count 64, bitcount 1, lookahead_consumed ≤ 64 – 1 = 63. , , « ; , ».

, : , 64- uint. 1 , ; , , . , , , , , RISC.

, , . , , , have_lookahead ; lookahead, lookahead.

3:

. , , refill/peek/consume, - . , ( ), . MSB:

 const uint8_t *bitptr; //     uint64_t bitbuf = 0; //    64  int bitpos = 0; //       void refill3_msb() { assert(bitpos <= 64); //        bitptr += bitpos >> 3; //  (Refill) bitbuf = read64BE(bitptr); //     ,     // (     ;   , //     .) bitpos &= 7; } uint64_t peekbits3_msb(int count) { assert(bitpos + count <= 64); assert(count >= 1 && count <= 64 - 7); //       uint64_t remaining = bitbuf << bitpos; //   "count"  return remaining >> (64 - count); } void consume3_msb(int count) { bitpos += count; } 

getbits , refill / peek / consume, , .

. «refill» «peek»/«consume», , . , ! , 64- big-endian ( x86 ARM). , ; . «lookahead».

4: lookahead

lookahead . , RAD Kraken ( : Yann, Xpack Kraken. , , , , . — . ). ( , refill ), ( , ), ; - , , ! , LSB-first, , LSB-first/MSB-first , .

 const uint8_t *bitptr; //        buf uint64_t bitbuf = 0; //     int bitcount = 0; //     void refill4_lsb() { //          //   . bitbuf |= read64LE(bitptr) << bitcount; //       bitptr += (63 - bitcount) >> 3; //     bitcount |= 56; // now bitcount is in [56,63] } uint64_t peekbits4_lsb(int count) { assert(count >= 0 && count <= 56); assert(count <= bitcount); return bitbuf & ((1ull << count) - 1); } void consume4_lsb(int count) { assert(count <= bitcount); bitbuf >>= count; bitcount -= count; } 

peek consume, - 56 .

refill, . 64 little-endian . bitptr / bitcount .

bitcount . , , refill 57 64 . , 56 63 ( ). But why? , refill bitcount - , 8; , bitcount & 7 ( 3 ) . refill, [56,63] , OR.

: ? bitcount :

• 56 ≤ bitcount ≤ 63, .
• 48 ≤ bitcount ≤ 55, 1 ( bit_ptr ).
• 40 ≤ bitcount ≤ 47, 2 .

. (63 - bitcount) >> 3 , bitptr .

bitbuf bitcount OR . , OR , . , (- consume), ; .

, , ? , , 3?

: , refill , bitcount . , refill. . , L1, ( 3-5 , ), bitcount - (. , ).

bitcount , , refill; , load ISA (, MSB-first little-endian ). , bitcount , , , .

, refill , . 2016 Kraken-, 10% ( refill , ).