Information systems with conceptual models. Part two
In the first part of the article, we started talking about a new class of high-level domain models, called conceptual ones. Unlike other similar models in conceptual models, the connections between concepts are concepts themselves, and the model is built on the basis of identifying and describing abstractions that have served to form the (definition) concepts of the subject domain. This allows end users to build and update domain models through simple and natural operations of creating, modifying, and deleting concepts and their entities.
Here, in the second part, we will talk about how a fully-functional information system can be implemented, based on conceptual modeling of subject areas. Now let's take a closer look at the LANCAD information system, which in our company “ INSISTEMS ” is used to organize the project activity for the development of design and estimate documentation for construction.
It should be noted that the emergence of the LANCAD information system was the result of the implementation of several major projects of the company.
')
Any information system in the presentation layer should use some formal language (formal theory) to describe the entities of the subject area modeled by it.
A great variety of languages ​​have been developed for textual representation of entities of the information system: XML (English Extensible Markup Language), JSON (English JavaScript Object Notation), XBRL (English Extensible Business Reporting Language), etc.
However, all these languages ​​have one significant drawback that hinders their effective use in information systems: they do not have expressive means to ensure recursive integrity. In other words, if a certain object or its descendants has a link to this object as a field, then the conversion of such an object into text can lead to an infinite loop or ignoring the link to this object.
This disadvantage is not possessed by the YAML (Yet Yet Markup Language) serialization language, which allows the description of recursive data structures by specifying anchors marking the reference object and aliases indicating the insertion points of references to an object marked with an anchor.
To solve the problem of efficiently describing recursive data structures that are present in conceptual models by definition, (one more) language NN (English Notion Notation) has been developed for textual representation of information system objects.
The text in the NN language is a sequence of comments and pairs of the “Name-Value” type with a divided “Equal” sign and ending with a “Sharp” sign, which are written with up to white space characters: “// x = y #” (a comment starting with two characters "Slash"), "x = y #" (name x with value y).
If the text “Name-Value” with the same name appears several times in the text, an array of values ​​of the same name is created. In turn, the description of an object (abstract concept), considered as a set of unordered sets of Name-Value pairs, always begins with the name of the object without specifying a value, after which the Name-Value pairs included in it are listed, and upon completion of the enumeration, Sharpe sign:
To indicate the reference to the previously described objects, unnamed values ​​are used that specify the path to the reference object, starting from the root (from the beginning of the description):
If you add additional Name-Value pairs in the reference object, they will replenish the reference object. This is useful when the reference object “must know” about its links or for objects that are partially defined at the time of the description.
The latter situation arose in the description of project plans, where a task as an object arises earlier, and the resources assigned to it are determined later. In this case, the description of the resource adds a link to the task to which the resource is attached, and the task itself is supplemented with a description of the resource assigned to it.
It should be noted that the names in NN are arbitrary sequences of characters, except for the "Equal" and "Sharp" signs, which, if they appear in the name, are enclosed in braces: "x {=} 5 = y #", "{#} x = y # ". In values, only the Sharpe sign is framed: “x = y {#} #”. You can use the empty name "= y" and the empty value "x = {} #".
If the name (value) has boundary whitespace characters, or the name is enclosed in curly brackets, or the name begins with two “slash” characters, or suppression of the interpretation of the value as a simple data type is required, then such name (value) is also framed with curly brackets: “{ x} = {{y}} # "," {// x} = y # "," x = {-132} # ".
This section is logical and philosophical. To whom this aspect is not interesting, they can skip the section. However, on issues that I received for the first part of the article, I judge the “advancement” of Habr's readers and am not sure that this section should be excluded from the article.
And so, let's continue ... Any formal language characterized by such properties as completeness and consistency.
The completeness of a formal language is considered as a property that characterizes the sufficiency of its expressive qualities for any purpose. To establish semantic completeness, a mapping is used which establishes the correspondence between the set of descriptions in a formal language and the entities of a certain subject domain, which is called the domain of interpretation. If a mapping is found, then such a formal language is called semantically complete with respect to this interpretation.
Along with the property of semantic completeness, another property is defined, which is considered as an internal property of the language itself, independent of any of its interpretations. A formal language is called syntactically complete if the set of descriptions it generates is sufficient for any interpretation domain.
It is known that the first-order predicate calculus (predicate logic) is the only formal language that is consistent and has fullness. While the arithmetic of natural numbers, although consistent, is no longer complete. And one cannot even say about set theory that it is consistent.
From here we conclude that all information systems that do not use the predicate calculus to model subject areas are possibly consistent, but essentially incomplete.
However, when using predicate calculus, an insurmountable problem of solvability arises (determining whether an arbitrary string belongs to a set of strings of a language) and it is difficult to overcome the problem of computability (the non-polynomial complexity of processing descriptions in a formal language).
For this reason, a narrowing of the predicate calculus has been found, called discourse logic, where the use of predicates with the number of arguments more than one is forbidden (the predicate is a logical function of subject variables). As a result, the problem of solvability disappeared. However, the problem of effective computability remains.
A natural question arises about the consistency, completeness, solvability and computability of the concept calculus used in the LANCAD information system and the language corresponding to this calculus.
First, find out what is the reason for the consistency and completeness of the predicate calculus. The concept of logical truth is quite definitely formulated by G. Leibniz. He called the formula logically true if it is true in all "worlds", i.e. in all interpretations. This means that logic does not contain any factual truths related to any particular "world."
The concept of logical truth clarified A. Tarsky. He showed that the term "true" expresses only the property of our knowledge, in particular, the property of statements, and not the reality itself. Consequently, the invariance of truth in various areas of interpretation results not from the properties of these areas, but from the properties of our consciousness.
Then, in addition to the predicate calculus, are there other semantic invariants? If we want to use the calculus of concepts to model arbitrary subject areas, then this calculus must be semantically invariant.
Recall that concepts are formed during abstraction. Abstracting is one of the forms of human mental activity, which allows one to mentally isolate and transform into independent representations individual properties, sides, elements or states of objects, processes and phenomena of the surrounding world.
It is obvious that the process of abstraction does not depend on any area of ​​interpretation, but is determined only by the qualities of the knowing subject himself. Then, on the basis of the formalization of the methods of education and the expression of concepts, a calculus can be constructed, which, like the predicate calculus, claims semantic invariance in all “imaginable worlds”.
In contrast to the predicate calculus, which has a domain of logical interpretation as a semantic invariant, the concept calculus is defined taking into account another semantic invariant - the domain of conceptual interpretation.
The consistency of the calculus of concepts is ensured by the absence in the conceptual structure of logical cycles or definitions of concepts, directly or indirectly through themselves. The latter is considered invalid in any formal or substantive theory claiming to be adequate.
The definition of logical cycles is carried out when creating a concept by verifying the conceptual structure. Since the number of concepts is finite, verification is a solvable problem. Obviously, all the tasks described earlier are solvable problems.
Thus, the LANCAD information system in the presentation layer uses a modeling language that is consistent, complete, decidable, and efficiently computable.
The basis of any information system designed for processing knowledge is the mechanism for representing knowledge and manipulating it in order to imitate a person’s reasoning to solve the set applied problems. In turn, a knowledge base is a database containing facts about a certain subject area, as well as inference rules, which allow to automatically derive conclusions based on the available facts and receive new statements about existing or newly entered facts.
An information system with a conceptual domain model can be considered as a knowledge base. In this case, the conceptual structure sets the rules for inference on knowledge, and the content of the concepts (rows of the corresponding tables) - the facts (judgments) about the subject area.
Data. Facts are statements about the ownership of a domain entity to a certain concept. In our case, an entity belongs to a concept if and only if the set of values ​​of attributes (attributes) of this entity is found as a row in the table of the corresponding concept.
Judgments . Judgments are statements with logical connectives "AND", "OR", "NOT", in which two types of predicates are used:
Inference. Any conclusion can be defined as a transition from one or several judgments constituting the premise of the conclusion to a statement - a consequence of the conclusion.
The rules for constructing inferences are defined by the inference rules that are accepted in the subject domain as generally significant, i.e. generating true statements for all possible assumptions. In logic, this rule is the well-known rule of Modus ponens: if A holds and A follows B, then B is true.
In our case, the rules for constructing inferences are defined by the rules of inference, which are stored in the conceptual structure, and the conceptual structure itself is considered as an informative theory of the subject domain, which preserves the truth of all the consequences derived from it.
It should be noted that the information system LANCAD implements the open world model, since in the process of its functioning the monotony of the output is disrupted. The conclusion is called monotonous, if for any statement obtained earlier when new facts come in, the derivability of this statement does not disappear.
Requests. To transform an information system into a full-fledged knowledge base, it is necessary to implement requests to extract facts (judgments) and derive assertions about the domain being modeled. Attention should be paid to the fact that all statements required for queries can be expressed in the language of the database.
In fig. 14 shows a simple query form designed to search for entities of a concept that satisfy the conditions specified using a template. The template consists of a list of attributes of the concept and is displayed in the left pane of the form when the pointer is set on the search node (the node with the Binoculars icon).
After specifying restrictions on the values ​​of one or several attributes, the information system searches for entities that satisfy the specified conditions and displays the latter as child nodes (marked in blue).
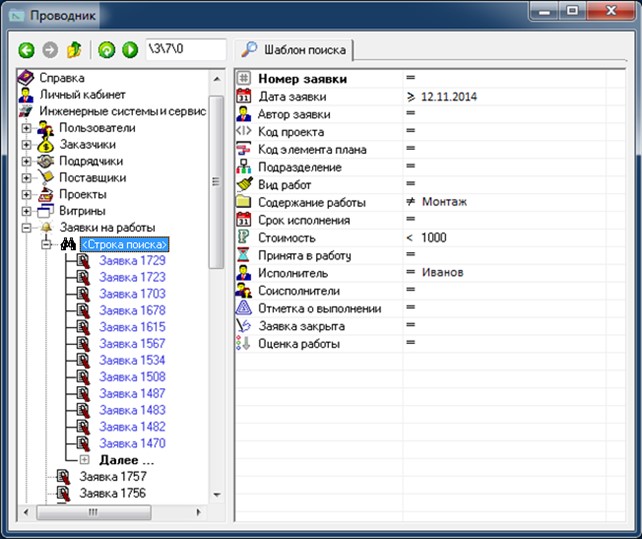Fig. 14. Search
A simplified search for the entities of a concept is carried out after entering the search string — an arbitrary sought-for substring — into the name of the search node (<Search string> in Fig. 14).
For more complex searches, queries are used to the knowledge base as a whole, and not just to one of its concepts. For this purpose, an appropriate interface and an output engine supporting it are provided. However, for many application queries, it is sufficient to use the address bar of the client application to find the conceptual structure of concepts by their names, followed by the search for the required entities in the tables of the found concepts.
In addition to the tasks of presenting, extracting and updating knowledge, there is another important task - their representation. The representation of knowledge consists in changing the form of their presentation and is carried out on the basis of the construction of conceptual sub-models with their subsequent processing (visualization) by special programs.
Not all the conceptual model is subject to processing (visualization). Therefore, the representation of knowledge requires the construction of some of its fragments. To do this, use the following procedure.
Initially, the entity or entities to be represented are specified.
Next, an initial approximation of the conceptual structure is constructed, which includes those concepts that are necessary to determine the initial entities.
Then the conceptual structure is replenished with concepts that are necessary to define concepts in their current set. Iterations are completed when the conceptual structure under construction ceases to be supplemented with new concepts.
At the end of the procedure, a description of the entities necessary for the representation of the concepts included in the constructed conceptual structure is created.
The submodel expressed in the NN language is transferred to the corresponding application that performs its processing, for example, visualization.
Project management. As an example of knowledge representation, consider the process of visualizing project plans. To manage projects, a conceptual model is built (Fig. 15), which uses such concepts as “Task” (“Tasks” tab), “Resource” (“Resources” tab), as well as links between tasks and assignment of resources to tasks (“ Plan").
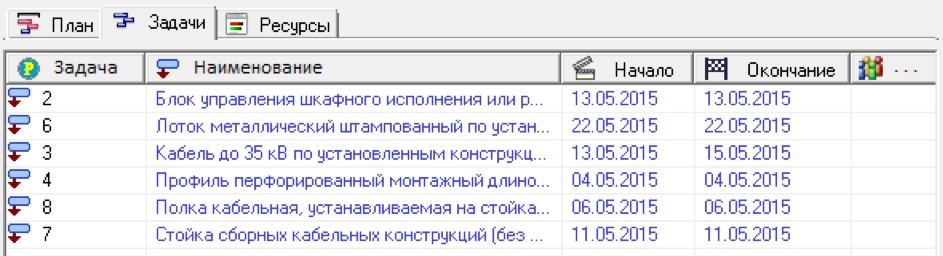Fig. 15. Conceptual model of the project plan
To display such a model, forms can be used that are implemented by the corresponding application programs: Gantt charts (Fig. 16), resource lists, graphs of resource use, etc. For this, the information system includes a module that renders the project plan based on its conceptual model using other applications.
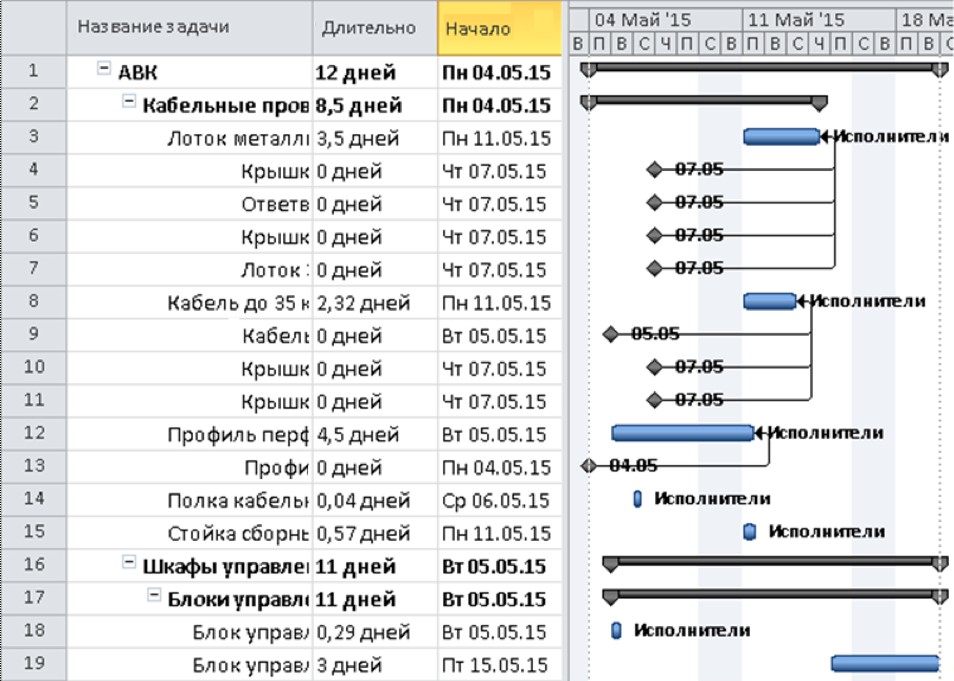Fig. 16. Visualization of the schedule
For visualized plans, feedback has also been implemented, in which changes made to the plan can update the conceptual model used to create such a plan.
Generation of documents. Another example of the use of conceptual models is the automatic creation of various kinds of documents. In this case, the represented model is used along with the rules for expressing concepts in the body of the document. The expressive means necessary for such a representation will depend on the desired form of display (text, graphics, sound, animation, etc.).
To display the conceptual model in a textual form, the rules for expressing concepts can be formed as a document template. When creating a template, a special markup language is used, which allows you to set the form of expression of concepts in the text.
In fig. 17 shows the formal grammar of the textual representation language of conceptual models, where the non-terminal language concepts are specified on the left before the “Arrow” sign, and their expression as a sequence of terminal and non-terminal concepts is defined on the right.
Fig. 17. Grammar of the text representation language
The grammar is given with an accuracy of whitespace, the optional occurrences of the concepts are enclosed in square brackets, and the alternative is shown with the sign “Vertical bar”. Terminal concepts are represented by strings enclosed in single quotes.
Template text consists of arbitrary strings and operators (rule 1). To represent the conceptual model, the operators of extraction, calculation, installation, selection and iteration are used (rule 2).
The extraction operator allows you to get and insert a formatted value at its location, which is extracted along a specified path in the conceptual model (rule 3). The calculation operator is used to represent, as text, the formatted value of some calculated expression (rule 4). The syntax and semantics of expressions are as in high-level languages.
The setup operator is used to change values ​​in the conceptual model and can be used, inter alia, to create temporary simple concepts or variables (rule 5). The choice operator is necessary for the implementation of textual branching in the process of model representation (rule 6), and the iteration operator is necessary for the representation of composite concepts (rule 7). Operators can be nested in each other, since all parts of the operators are plain text.
As an example in fig. 18 the document template is shown, and on fig. 19 - the document itself, resulting from the representation of a certain conceptual model.
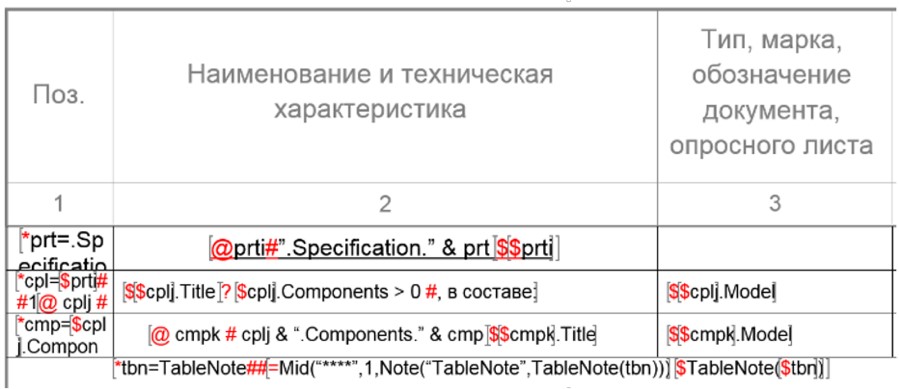Fig. 18. Document Template
Fig. 19. Text document
Other forms of representation. In a similar way, conceptual models of other stable fragments of subject areas are created for their representation in the appropriate form, for example:
“We encode little by little” is an allusion to the statement of the inventor of the heuristic machine for “answering any questions” Mashkin Edelweiss Zakharovich from the story A. and B. Strugatsky “The Tale of the Three”.
Let's discuss the methods and means of solving problems on conceptual models for obtaining answers that are not directly contained in them. The form of such answers can no longer be a statement. To obtain statements, the knowledge-based output is used. Nothing else remains, except that the result of solving an applied task will be the generation of new knowledge, expressed in the form of an actualized or newly created conceptual model.
Abstracting from the specific content of the actions that constitute the algorithms for solving a particular applied problem, we can conclude that all such algorithms are formulated through the previously considered operations on concepts. Otherwise, it is necessary to present a description of the algorithm that would not be expressed at the conceptual level. Obviously, the presence of such a description, and even his search itself look absurd.
Thus, the semantically invariant (independent of the domain) form for describing the solutions of any applied problems in the presentation layer is an algorithm consisting of three elementary operations on the essence of concepts.
It is necessary to separately distinguish the concept-values ​​on which operations can be performed, provided for the corresponding data type. For example, standard arithmetic operations should be provided for numbers, string concatenation, searching for a substring and replacing it with another substring, etc., should be provided for strings.
As an example of solving problems on conceptual models, we consider the following problem. It is known that one of the main documents of the working documentation for construction is the specification of products, equipment and materials (Fig. 20).
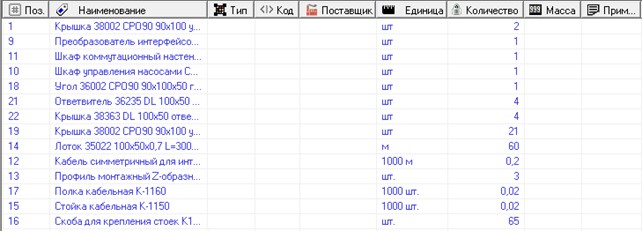Fig. 20. Specification
Often there is a problem, using the base of estimated standards, to obtain from it a local estimate for the production of work (Fig. 21).
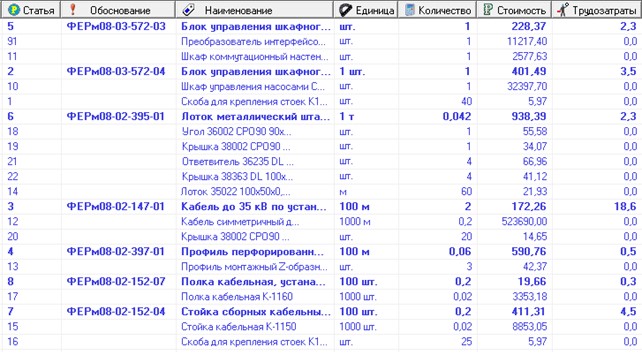Fig. 21. Estimates
To solve this problem, a special module has been developed and is used, which is loaded from the database layer and executed in the presentation layer (Fig. 22).
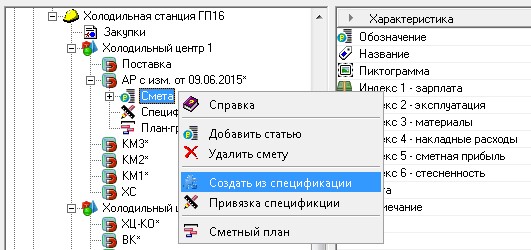Fig. 22. Calling up the budget creation module.
Attention should be paid to the fact that the information system itself also has a certain conceptual model, which is handled through the client application (Fig. 23). This model may include such concepts as:
Fig. 23 - Client Application
This article describes the construction of an information system with a conceptual domain model. Domain models are called conceptual to distinguish them from well-known conceptual models. In conceptual models, concepts (concepts) and all sorts of connections (relationships) between them that carry part of the semantic load of the model are defined. Another part of the semantics of the conceptual model is contained in additional data, which define relationships between concepts in the form of logical expressions, formulas, functions, etc.
In conceptual models, the connections between concepts are themselves concepts, and the model is built on the basis of identifying and describing abstractions that have served to form concepts (definitions). The refusal to describe associations in the form of links with different semantic markup makes the conceptual structure of the subject area representable in the form of a tree and more visual.
The subject semantics is fully defined by the conceptual structure, and the attributes of the concepts determine nothing more than the structuredness of the descriptions of the concepts in the database layer. In this case, it is not necessary to set logical statements (formulas, functions) that characterize concepts and are rules of inference. Everything that is necessary for a conclusion on knowledge is contained in the conceptual structure of the subject area and tables of concepts.
Thus, the fundamental difference of the considered approach is to use, in addition to logic, another semantic invariant - the rules of formation and expression of concepts. This required the definition of associations (connections) between concepts in the form of independent concepts.
Other important advantages of information systems with conceptual modeling of the subject area are:
As a result, an information system with conceptual modeling of the subject area is a representative of a new generation of information systems in the methodological, technological and operational terms. Using the conceptual model creates the prerequisites for improving the transparency of business processes of an enterprise, helps to optimize costs and increase investment attractiveness, reduces the risks of owning an information system, namely:
Here, in the second part, we will talk about how a fully-functional information system can be implemented, based on conceptual modeling of subject areas. Now let's take a closer look at the LANCAD information system, which in our company “ INSISTEMS ” is used to organize the project activity for the development of design and estimate documentation for construction.
It should be noted that the emergence of the LANCAD information system was the result of the implementation of several major projects of the company.
')
My tongue my friend
Any information system in the presentation layer should use some formal language (formal theory) to describe the entities of the subject area modeled by it.
A great variety of languages ​​have been developed for textual representation of entities of the information system: XML (English Extensible Markup Language), JSON (English JavaScript Object Notation), XBRL (English Extensible Business Reporting Language), etc.
However, all these languages ​​have one significant drawback that hinders their effective use in information systems: they do not have expressive means to ensure recursive integrity. In other words, if a certain object or its descendants has a link to this object as a field, then the conversion of such an object into text can lead to an infinite loop or ignoring the link to this object.
This disadvantage is not possessed by the YAML (Yet Yet Markup Language) serialization language, which allows the description of recursive data structures by specifying anchors marking the reference object and aliases indicating the insertion points of references to an object marked with an anchor.
To solve the problem of efficiently describing recursive data structures that are present in conceptual models by definition, (one more) language NN (English Notion Notation) has been developed for textual representation of information system objects.
The text in the NN language is a sequence of comments and pairs of the “Name-Value” type with a divided “Equal” sign and ending with a “Sharp” sign, which are written with up to white space characters: “// x = y #” (a comment starting with two characters "Slash"), "x = y #" (name x with value y).
As values, the language allows the values ​​of simple data types:
- integers (13, -2),
- fractional numbers (-3.557),
- floating point numbers (1.2e-12),
- of time (12:34, 2: 3: 4.1),
- days (04/12/2018, 2018-12-04, 04/12/2018),
- Dates (04/12/2018 12:34, 2018-12-04 2: 3: 4, 04/12/2018 2: 3: 4.1)
- characters (a, i, \),
- lines (abbreviated),
- binary data (0x34DF48FA87D139B3EE2378),
- functions ((x): x + 1, (x, y): x * y).
If the text “Name-Value” with the same name appears several times in the text, an array of values ​​of the same name is created. In turn, the description of an object (abstract concept), considered as a set of unordered sets of Name-Value pairs, always begins with the name of the object without specifying a value, after which the Name-Value pairs included in it are listed, and upon completion of the enumeration, Sharpe sign:
// x #
x = #
a = 12.4 #
b = 12.4e-1 #
c = 3:4:5 #
d = 12.4.2018 #
e = 12.4.2018 3:4:5 #
f = #
g = #
h = 0x34DF48FA87D139B3EE2378 #
// i, a x #
i = (a): a * $.a #
// j #
j = 1 #
j = 3:4:5 #
j = #
u = -2.5 #
v = abcd #
#
#
To indicate the reference to the previously described objects, unnamed values ​​are used that specify the path to the reference object, starting from the root (from the beginning of the description):
// x #
x = #
// xy #
y = #
// xyz = xy #
z = #
// xy #
x # y #
// xy #
c = 12 #
#
// c = 12 #
#
#
If you add additional Name-Value pairs in the reference object, they will replenish the reference object. This is useful when the reference object “must know” about its links or for objects that are partially defined at the time of the description.
The latter situation arose in the description of project plans, where a task as an object arises earlier, and the resources assigned to it are determined later. In this case, the description of the resource adds a link to the task to which the resource is attached, and the task itself is supplemented with a description of the resource assigned to it.
It should be noted that the names in NN are arbitrary sequences of characters, except for the "Equal" and "Sharp" signs, which, if they appear in the name, are enclosed in braces: "x {=} 5 = y #", "{#} x = y # ". In values, only the Sharpe sign is framed: “x = y {#} #”. You can use the empty name "= y" and the empty value "x = {} #".
If the name (value) has boundary whitespace characters, or the name is enclosed in curly brackets, or the name begins with two “slash” characters, or suppression of the interpretation of the value as a simple data type is required, then such name (value) is also framed with curly brackets: “{ x} = {{y}} # "," {// x} = y # "," x = {-132} # ".
What is true in all worlds
This section is logical and philosophical. To whom this aspect is not interesting, they can skip the section. However, on issues that I received for the first part of the article, I judge the “advancement” of Habr's readers and am not sure that this section should be excluded from the article.
And so, let's continue ... Any formal language characterized by such properties as completeness and consistency.
The completeness of a formal language is considered as a property that characterizes the sufficiency of its expressive qualities for any purpose. To establish semantic completeness, a mapping is used which establishes the correspondence between the set of descriptions in a formal language and the entities of a certain subject domain, which is called the domain of interpretation. If a mapping is found, then such a formal language is called semantically complete with respect to this interpretation.
Along with the property of semantic completeness, another property is defined, which is considered as an internal property of the language itself, independent of any of its interpretations. A formal language is called syntactically complete if the set of descriptions it generates is sufficient for any interpretation domain.
It is known that the first-order predicate calculus (predicate logic) is the only formal language that is consistent and has fullness. While the arithmetic of natural numbers, although consistent, is no longer complete. And one cannot even say about set theory that it is consistent.
From here we conclude that all information systems that do not use the predicate calculus to model subject areas are possibly consistent, but essentially incomplete.
However, when using predicate calculus, an insurmountable problem of solvability arises (determining whether an arbitrary string belongs to a set of strings of a language) and it is difficult to overcome the problem of computability (the non-polynomial complexity of processing descriptions in a formal language).
For this reason, a narrowing of the predicate calculus has been found, called discourse logic, where the use of predicates with the number of arguments more than one is forbidden (the predicate is a logical function of subject variables). As a result, the problem of solvability disappeared. However, the problem of effective computability remains.
A natural question arises about the consistency, completeness, solvability and computability of the concept calculus used in the LANCAD information system and the language corresponding to this calculus.
First, find out what is the reason for the consistency and completeness of the predicate calculus. The concept of logical truth is quite definitely formulated by G. Leibniz. He called the formula logically true if it is true in all "worlds", i.e. in all interpretations. This means that logic does not contain any factual truths related to any particular "world."
The concept of logical truth clarified A. Tarsky. He showed that the term "true" expresses only the property of our knowledge, in particular, the property of statements, and not the reality itself. Consequently, the invariance of truth in various areas of interpretation results not from the properties of these areas, but from the properties of our consciousness.
Then, in addition to the predicate calculus, are there other semantic invariants? If we want to use the calculus of concepts to model arbitrary subject areas, then this calculus must be semantically invariant.
Recall that concepts are formed during abstraction. Abstracting is one of the forms of human mental activity, which allows one to mentally isolate and transform into independent representations individual properties, sides, elements or states of objects, processes and phenomena of the surrounding world.
It is obvious that the process of abstraction does not depend on any area of ​​interpretation, but is determined only by the qualities of the knowing subject himself. Then, on the basis of the formalization of the methods of education and the expression of concepts, a calculus can be constructed, which, like the predicate calculus, claims semantic invariance in all “imaginable worlds”.
In contrast to the predicate calculus, which has a domain of logical interpretation as a semantic invariant, the concept calculus is defined taking into account another semantic invariant - the domain of conceptual interpretation.
The consistency of the calculus of concepts is ensured by the absence in the conceptual structure of logical cycles or definitions of concepts, directly or indirectly through themselves. The latter is considered invalid in any formal or substantive theory claiming to be adequate.
The definition of logical cycles is carried out when creating a concept by verifying the conceptual structure. Since the number of concepts is finite, verification is a solvable problem. Obviously, all the tasks described earlier are solvable problems.
Thus, the LANCAD information system in the presentation layer uses a modeling language that is consistent, complete, decidable, and efficiently computable.
When data is knowledge
The basis of any information system designed for processing knowledge is the mechanism for representing knowledge and manipulating it in order to imitate a person’s reasoning to solve the set applied problems. In turn, a knowledge base is a database containing facts about a certain subject area, as well as inference rules, which allow to automatically derive conclusions based on the available facts and receive new statements about existing or newly entered facts.
An information system with a conceptual domain model can be considered as a knowledge base. In this case, the conceptual structure sets the rules for inference on knowledge, and the content of the concepts (rows of the corresponding tables) - the facts (judgments) about the subject area.
Data. Facts are statements about the ownership of a domain entity to a certain concept. In our case, an entity belongs to a concept if and only if the set of values ​​of attributes (attributes) of this entity is found as a row in the table of the corresponding concept.
For example, if there is a table in the database describing users, and there is a specific user, then knowing his attributes (name and password) is easy to determine whether he is a user of the information system. For this, the table must contain an entry with the name and password of this user.
Judgments . Judgments are statements with logical connectives "AND", "OR", "NOT", in which two types of predicates are used:
- single predicates N (E) of determining the belonging of the essence E to the concept N;
- relations of the form P [E] * V, where P [E] is a functor that returns the value of the attribute P of the entity E, * is the sign of the relation (=,! =,>,> =, <, <=, etc.), V is the essence of some concept.
For example, “Ivanov - the Employee”, and in the predicate form the Employee (Ivanov). Or "Attribute Password Petrov is equal to *****".
Inference. Any conclusion can be defined as a transition from one or several judgments constituting the premise of the conclusion to a statement - a consequence of the conclusion.
The rules for constructing inferences are defined by the inference rules that are accepted in the subject domain as generally significant, i.e. generating true statements for all possible assumptions. In logic, this rule is the well-known rule of Modus ponens: if A holds and A follows B, then B is true.
In our case, the rules for constructing inferences are defined by the rules of inference, which are stored in the conceptual structure, and the conceptual structure itself is considered as an informative theory of the subject domain, which preserves the truth of all the consequences derived from it.
Consider a simple example. Suppose there is a conceptual model that describes the staff structure of the company. In this model, there may be such concepts as Trainee, Employee, Position, Division, Employee (concept-synthesis of concepts Trainee and Employee) and Staff (concept-association of concepts Division, Position, Employee). Then, in a regular-official world, judgments of the form “X (some entity) are Trainee (Employee, Office, Division, Employee, State)” are possible, and conclusions of the form “if (A, B, C) is the essence of the concept Staff, then A - Division, B - Position, C - Worker "and any derivatives of it, where one or several judgments are left in the conclusion, as well as" if X is an Intern (Employee), then X is an Employee "and" if X is an Employee, then X - Employee or X - Intern.
It should be noted that the information system LANCAD implements the open world model, since in the process of its functioning the monotony of the output is disrupted. The conclusion is called monotonous, if for any statement obtained earlier when new facts come in, the derivability of this statement does not disappear.
Requests. To transform an information system into a full-fledged knowledge base, it is necessary to implement requests to extract facts (judgments) and derive assertions about the domain being modeled. Attention should be paid to the fact that all statements required for queries can be expressed in the language of the database.
In fig. 14 shows a simple query form designed to search for entities of a concept that satisfy the conditions specified using a template. The template consists of a list of attributes of the concept and is displayed in the left pane of the form when the pointer is set on the search node (the node with the Binoculars icon).
After specifying restrictions on the values ​​of one or several attributes, the information system searches for entities that satisfy the specified conditions and displays the latter as child nodes (marked in blue).
A simplified search for the entities of a concept is carried out after entering the search string — an arbitrary sought-for substring — into the name of the search node (<Search string> in Fig. 14).
For more complex searches, queries are used to the knowledge base as a whole, and not just to one of its concepts. For this purpose, an appropriate interface and an output engine supporting it are provided. However, for many application queries, it is sufficient to use the address bar of the client application to find the conceptual structure of concepts by their names, followed by the search for the required entities in the tables of the found concepts.
Not a single logic ...
In addition to the tasks of presenting, extracting and updating knowledge, there is another important task - their representation. The representation of knowledge consists in changing the form of their presentation and is carried out on the basis of the construction of conceptual sub-models with their subsequent processing (visualization) by special programs.
Not all the conceptual model is subject to processing (visualization). Therefore, the representation of knowledge requires the construction of some of its fragments. To do this, use the following procedure.
Initially, the entity or entities to be represented are specified.
Next, an initial approximation of the conceptual structure is constructed, which includes those concepts that are necessary to determine the initial entities.
Then the conceptual structure is replenished with concepts that are necessary to define concepts in their current set. Iterations are completed when the conceptual structure under construction ceases to be supplemented with new concepts.
At the end of the procedure, a description of the entities necessary for the representation of the concepts included in the constructed conceptual structure is created.
The submodel expressed in the NN language is transferred to the corresponding application that performs its processing, for example, visualization.
Project management. As an example of knowledge representation, consider the process of visualizing project plans. To manage projects, a conceptual model is built (Fig. 15), which uses such concepts as “Task” (“Tasks” tab), “Resource” (“Resources” tab), as well as links between tasks and assignment of resources to tasks (“ Plan").
To display such a model, forms can be used that are implemented by the corresponding application programs: Gantt charts (Fig. 16), resource lists, graphs of resource use, etc. For this, the information system includes a module that renders the project plan based on its conceptual model using other applications.
For visualized plans, feedback has also been implemented, in which changes made to the plan can update the conceptual model used to create such a plan.
Generation of documents. Another example of the use of conceptual models is the automatic creation of various kinds of documents. In this case, the represented model is used along with the rules for expressing concepts in the body of the document. The expressive means necessary for such a representation will depend on the desired form of display (text, graphics, sound, animation, etc.).
To display the conceptual model in a textual form, the rules for expressing concepts can be formed as a document template. When creating a template, a special markup language is used, which allows you to set the form of expression of concepts in the text.
In fig. 17 shows the formal grammar of the textual representation language of conceptual models, where the non-terminal language concepts are specified on the left before the “Arrow” sign, and their expression as a sequence of terminal and non-terminal concepts is defined on the right.
The grammar is given with an accuracy of whitespace, the optional occurrences of the concepts are enclosed in square brackets, and the alternative is shown with the sign “Vertical bar”. Terminal concepts are represented by strings enclosed in single quotes.
Template text consists of arbitrary strings and operators (rule 1). To represent the conceptual model, the operators of extraction, calculation, installation, selection and iteration are used (rule 2).
The extraction operator allows you to get and insert a formatted value at its location, which is extracted along a specified path in the conceptual model (rule 3). The calculation operator is used to represent, as text, the formatted value of some calculated expression (rule 4). The syntax and semantics of expressions are as in high-level languages.
The setup operator is used to change values ​​in the conceptual model and can be used, inter alia, to create temporary simple concepts or variables (rule 5). The choice operator is necessary for the implementation of textual branching in the process of model representation (rule 6), and the iteration operator is necessary for the representation of composite concepts (rule 7). Operators can be nested in each other, since all parts of the operators are plain text.
As an example in fig. 18 the document template is shown, and on fig. 19 - the document itself, resulting from the representation of a certain conceptual model.
Other forms of representation. In a similar way, conceptual models of other stable fragments of subject areas are created for their representation in the appropriate form, for example:
- graphs and charts (graphical representation of data in line segments or geometric shapes);
- ( , , , ..);
- ( , , );
- - ( ).
“We encode little by little” is an allusion to the statement of the inventor of the heuristic machine for “answering any questions” Mashkin Edelweiss Zakharovich from the story A. and B. Strugatsky “The Tale of the Three”.
Let's discuss the methods and means of solving problems on conceptual models for obtaining answers that are not directly contained in them. The form of such answers can no longer be a statement. To obtain statements, the knowledge-based output is used. Nothing else remains, except that the result of solving an applied task will be the generation of new knowledge, expressed in the form of an actualized or newly created conceptual model.
Abstracting from the specific content of the actions that constitute the algorithms for solving a particular applied problem, we can conclude that all such algorithms are formulated through the previously considered operations on concepts. Otherwise, it is necessary to present a description of the algorithm that would not be expressed at the conceptual level. Obviously, the presence of such a description, and even his search itself look absurd.
Thus, the semantically invariant (independent of the domain) form for describing the solutions of any applied problems in the presentation layer is an algorithm consisting of three elementary operations on the essence of concepts.
It is necessary to separately distinguish the concept-values ​​on which operations can be performed, provided for the corresponding data type. For example, standard arithmetic operations should be provided for numbers, string concatenation, searching for a substring and replacing it with another substring, etc., should be provided for strings.
As an example of solving problems on conceptual models, we consider the following problem. It is known that one of the main documents of the working documentation for construction is the specification of products, equipment and materials (Fig. 20).
Often there is a problem, using the base of estimated standards, to obtain from it a local estimate for the production of work (Fig. 21).
To solve this problem, a special module has been developed and is used, which is loaded from the database layer and executed in the presentation layer (Fig. 22).
Attention should be paid to the fact that the information system itself also has a certain conceptual model, which is handled through the client application (Fig. 23). This model may include such concepts as:
- a module that is connected during the operation of the client application and serves to implement a specific function of displaying a conceptual model or solving a specific task of the domain;
- an event that is registered in the information system and allows you to specify a handler for the operations of creating, deleting, or changing concepts;
- form created for the implementation of various specific user input scenarios;
- other concepts necessary to implement the requirements for a particular subject area model.
In conclusion: the challenges and advantages
This article describes the construction of an information system with a conceptual domain model. Domain models are called conceptual to distinguish them from well-known conceptual models. In conceptual models, concepts (concepts) and all sorts of connections (relationships) between them that carry part of the semantic load of the model are defined. Another part of the semantics of the conceptual model is contained in additional data, which define relationships between concepts in the form of logical expressions, formulas, functions, etc.
In conceptual models, the connections between concepts are themselves concepts, and the model is built on the basis of identifying and describing abstractions that have served to form concepts (definitions). The refusal to describe associations in the form of links with different semantic markup makes the conceptual structure of the subject area representable in the form of a tree and more visual.
The subject semantics is fully defined by the conceptual structure, and the attributes of the concepts determine nothing more than the structuredness of the descriptions of the concepts in the database layer. In this case, it is not necessary to set logical statements (formulas, functions) that characterize concepts and are rules of inference. Everything that is necessary for a conclusion on knowledge is contained in the conceptual structure of the subject area and tables of concepts.
Thus, the fundamental difference of the considered approach is to use, in addition to logic, another semantic invariant - the rules of formation and expression of concepts. This required the definition of associations (connections) between concepts in the form of independent concepts.
Other important advantages of information systems with conceptual modeling of the subject area are:
- Transparency - the use of extremely general and natural methods of analysis of the subject area, the unification of the enterprise survey before the introduction of the information system;
- customizability - the ability to take into account the sectoral specifics of enterprises, the applicability of enterprises of any size and scope of activity, speed and gradual implementation;
- – , , ;
- – , , ;
- – , ;
- – , ;
- – , .
– , .
As a result, an information system with conceptual modeling of the subject area is a representative of a new generation of information systems in the methodological, technological and operational terms. Using the conceptual model creates the prerequisites for improving the transparency of business processes of an enterprise, helps to optimize costs and increase investment attractiveness, reduces the risks of owning an information system, namely:
- project risks associated with the creation of an information system;
- technological risks associated with the loss or distortion of data in the process of updating the model;
- operational risks associated with maintaining the information system in working condition and ensuring vendor independence;
- escort risks associated with subject matter variability.
I remind about our vacancies.
Source: https://habr.com/ru/post/359088/
All Articles