Chromatic number of the plane is not less than 5
The problem of the chromatic number of a plane is formulated as follows: what is the smallest number of colors that can be colored on a plane so that any two points at a distance of 1 are painted in different colors?
This task was formulated by Hugo Hadwiger and Pal Erdos in the forties of the 20th century. Regardless of them, at about the same time, Edward Nelson and J. R. Isbell were engaged in this task. After the work of Hadwiger of 1961 on open problems at that time, the chromatic number of the plane began to be actively studied.
It was immediately shown that in 3 colors the plane cannot be painted in the required way, however 7 colors are enough. Indeed, it is easy to choose several points on a plane so that some of them are at a distance of exactly 1 (such a construction of points is called the unit distance graph ), and then by searching it is impossible to show that in 3 colors these points cannot be colored. Examples of such graphs - the spindle of Moser and the graph of Golomb are shown in the picture below. To show that 7 colors are enough, we will divide the plane with regular hexagons with a side of 0.4 and paint them in a certain pattern, as in the picture below. Then, as it is easy to see, the ends of any segment of length 1 will lie in different hexagons of different colors.
')

However, since then no one has been able to clarify either the upper or the lower boundaries. The task is called the Nelson-Erd os-Hadwiger Problem . 60 years have passed, and now, in April 2018, amateur mathematician Aubrey de Gray presented a graph of unit distances, which cannot be painted in 4 colors.
 Aubrey David Nicholas Jasper di Gray is a British gerontologist who explores various aspects of human aging. He is the developer of the SENS concept - “strategies for achieving negligible aging by engineering methods” (strategies for engineered negligible senescence). Chairman and Director of Science of the SENS Foundation, editor-in-chief of the academic journal Rejuvenation Research. The author of the popular science book "Ending Aging", which discusses in detail the question of a complete victory over aging by means of medicine over the next few decades. (info from wiki)
Aubrey David Nicholas Jasper di Gray is a British gerontologist who explores various aspects of human aging. He is the developer of the SENS concept - “strategies for achieving negligible aging by engineering methods” (strategies for engineered negligible senescence). Chairman and Director of Science of the SENS Foundation, editor-in-chief of the academic journal Rejuvenation Research. The author of the popular science book "Ending Aging", which discusses in detail the question of a complete victory over aging by means of medicine over the next few decades. (info from wiki)
As it turned out, this venerable bearded uncle also enjoys mathematics in his spare time. On April 8, 2018, he laid out an article on arXiv, in which he describes a method for constructing a graph of unit distances, which requires at least 5 colors to be painted.
Let's take a closer look at what kind of graph it is.
It all starts with a simple graph H consisting of 7 vertices and 12 edges:

Let's try to paint it in no more than 4 colors in various ways. It turns out that there are only 4 different ways to do this (up to turns, reflections and color order):

Note that in the upper two versions we have triples of monochrome vertices, which are located at the vertices of a regular triangle, and at the lower two, they are not. We call the coloring of the graph H bad if there is such a monochrome triple there, otherwise the coloring of H is good. Total, we have 2 bad coloring and 2 good.
Ok, go ahead. Consider a graph J, glued from 13 graphs H (find them all!):
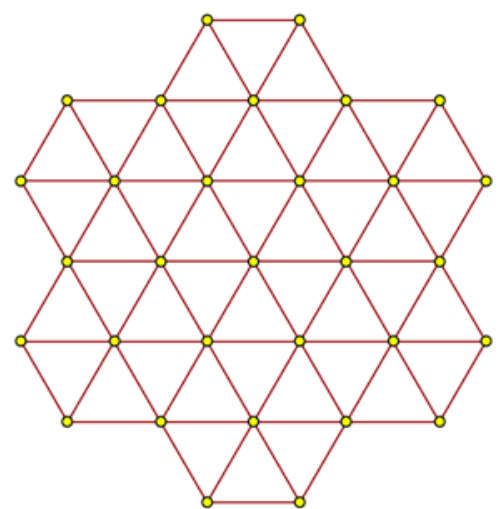
Let's try to color graph J so that the colors of all the subgraphs of H included in it are good. A little patience, and we get 6 different variations (again, up to any equivalent transformations mentioned above; plus the colors of the vertices marked in black):

Black peaks can be painted in several ways, but painting them is not particularly important to us. Nevertheless, it is undesirable to throw them out of the J column - then “extra” painting options appear. Which, moreover, spoil all further constructions. Therefore, let the black peaks remain.
Now let's take a closer look at the resulting options. Namely, on the central vertex and on the 6 vertices, which are at a distance of 2 from the central one (a sort of graph H, doubled). We see that there are always used no more than two colors. Moreover, all options can be divided into 3 cases:
Let us remember these observations and move on to the graph K, which is composed of two copies of the graph J as follows: we superimpose one copy J on another so that the central vertices coincide, and then we twist them relative to each other so that each of the 6 vertices that we considered a little higher, one graph drove off from the corresponding vertex of another graph at a distance of exactly 1 (I noted these distances just below in blue). And here he is Count K:

Already getting a little difficult, isn't it?
Now let's again meditate a little on the resulting structure. Namely, let us understand what types of colorings for each copy of the graph J could be of the three that were listed above. Type a) there are no coloring pages, since whatever type the second copy is, we get two vertices of the same color at a distance of 1. Type b) are not there either: if the second copy is also type b), then some 2 vertices center colors "interfere" with each other; if the second copy has type c), then at least one vertex at the ends of the one-color diagonal will correspond to one of the four vertices of the first copy. Therefore, both copies of the graph J are painting type c)! And such paints are possible, because 4 vertices, which are painted in a color different from the central one, although they have the same color, in each of the copies this color may be different.
Now, since two copies of the graph J in the graph K contain type c), then the pairs of opposite vertices (out of 6 considered in each copy) have the same color. We take advantage of this observation and take another step. Namely, we construct the graph L from two copies of the graph K:
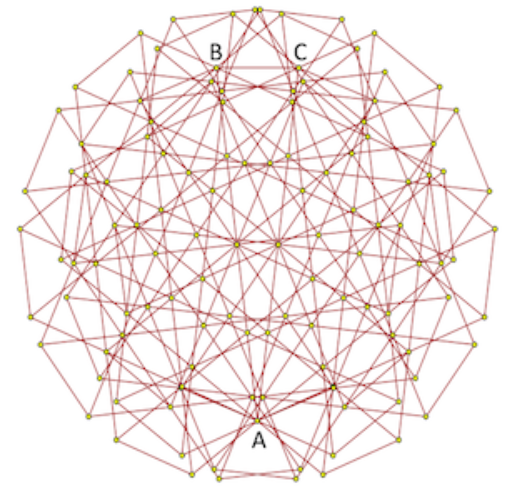
We superimpose the graphs K on each other as follows: we take in each of them a pair of opposite vertices and combine the first vertices in each pair (in the picture above it is marked with A), and the second ones are placed at a distance of exactly 1 (they are marked with B and C) . This technique is called overlapping of the graph (from the English. Spindling, where spindle is a spindle). For example, the Moser spindle is an overlap of a graph-rhombus composed of two triangles. Observing a little higher, the vertices A, B and C should be the same color, B and C at a distance of 1, so the graph L cannot be colored.
So what, we have proved everything? No, we just proved that the graph L cannot be painted in 4 colors so that the colors of all copies of the graph H (and there are already 52 of them!) Were good. Hence, in any painting of a graph L, painting of at least one graph H will be bad !
This part, unfortunately, cannot be sorted out without the help of a computer. Therefore, we briefly analyze the further part of the constructions, for details you can refer to the original article, or by clicking on the links to Polymath below. The pictures taken from the original article are not of very high quality, but they make it possible to approximately understand what is happening.
So, first we build the graph V on 31 vertices, which consists of 5 graphs H, which are aligned with the centers and rotated to cunning angles relative to each other:

Next, we build the graph W as follows: make 31 copies of the graph V and place the center of each copy at each vertex of another graph V (this operation is called the Minkowski sum of two unit distance graphs, that is, we do ), after which we delete all vertices that are more than a distance from the center . So now we have a graph W for 301 vertices:

Now take the graph H and replace each of its vertices with a copy of the graph W (i.e., do ). As a result, we obtain the graph M at 1345 vertices:

The resulting graph M is essentially the union of a large heap of Moser's spindles in various positions. And, if we paint three vertices in one color at a pairwise distance of the original graph H, which we fluffed up to M, thus making the painting H bad, then the rest of the graph M cannot be painted in 4 colors. This fact is verified by computer search.
And finally, the last step: we now take this tin M at 1345 vertices and copy over each of the 52 copies of the graph H in the graph L. As a result, we get a full tin at 20425 vertices, which is called the graph N. And this graph cannot be painted in 4 colors: when painting a frame L, painting at least one of the subgraphs H will turn out to be bad, and for this subgraph H the corresponding copy M will not be completed to make up to the end.
Q.E.D.
The graph at 20,425 vertices is a fairly large graph. Is it possible to build a smaller example? Can! In the original article, de Gray reduced the example to 1581 vertices with various cutoffs.
After the publication of the article, the mathematical community organized the Polymath16 project (as it was, for example, with the problem of prime numbers of twins ) in order to collectively reduce the graph obtained by de Gray to generalize the result to higher dimensions (for three-dimensional space, four-dimensional, and further), or even improve the lower limit of the chromatic number for the plane to 6.
By the way, in the same place they independently checked with the help of SAT-solvers that the example of de Gray on 1581 vertices can really be painted only in 5 colors, and also that its graph is a unit distance graph. So there is no doubt about the correctness of the result.
Graf de Gray is slowly decreasing. For example, the graph L by 121 vertices and 52 copies of the graph H can be slightly reduced to the graph L 'by 97 vertices and 40 copies of the graph H. The graph M with 1345 vertices has been reduced to the graph M' with only 278 vertices.
After replacing all the subgraphs H by M 'and the column L', the result can be improved further. At the time of this writing, the smallest unit distance graph found, which cannot be painted in 4 colors, has 610 vertices. Here is his picture (clickable):
Work continues. Maybe soon it will be possible to build a graph of unit distances, which can not be painted in 5 colors. And then - at 6, and then the problem of the chromatic number of the plane will be completely solved.
This task was formulated by Hugo Hadwiger and Pal Erdos in the forties of the 20th century. Regardless of them, at about the same time, Edward Nelson and J. R. Isbell were engaged in this task. After the work of Hadwiger of 1961 on open problems at that time, the chromatic number of the plane began to be actively studied.
It was immediately shown that in 3 colors the plane cannot be painted in the required way, however 7 colors are enough. Indeed, it is easy to choose several points on a plane so that some of them are at a distance of exactly 1 (such a construction of points is called the unit distance graph ), and then by searching it is impossible to show that in 3 colors these points cannot be colored. Examples of such graphs - the spindle of Moser and the graph of Golomb are shown in the picture below. To show that 7 colors are enough, we will divide the plane with regular hexagons with a side of 0.4 and paint them in a certain pattern, as in the picture below. Then, as it is easy to see, the ends of any segment of length 1 will lie in different hexagons of different colors.
')

However, since then no one has been able to clarify either the upper or the lower boundaries. The task is called the Nelson-Erd os-Hadwiger Problem . 60 years have passed, and now, in April 2018, amateur mathematician Aubrey de Gray presented a graph of unit distances, which cannot be painted in 4 colors.
Gerontology and Mathematics
 Aubrey David Nicholas Jasper di Gray is a British gerontologist who explores various aspects of human aging. He is the developer of the SENS concept - “strategies for achieving negligible aging by engineering methods” (strategies for engineered negligible senescence). Chairman and Director of Science of the SENS Foundation, editor-in-chief of the academic journal Rejuvenation Research. The author of the popular science book "Ending Aging", which discusses in detail the question of a complete victory over aging by means of medicine over the next few decades. (info from wiki)
Aubrey David Nicholas Jasper di Gray is a British gerontologist who explores various aspects of human aging. He is the developer of the SENS concept - “strategies for achieving negligible aging by engineering methods” (strategies for engineered negligible senescence). Chairman and Director of Science of the SENS Foundation, editor-in-chief of the academic journal Rejuvenation Research. The author of the popular science book "Ending Aging", which discusses in detail the question of a complete victory over aging by means of medicine over the next few decades. (info from wiki)As it turned out, this venerable bearded uncle also enjoys mathematics in his spare time. On April 8, 2018, he laid out an article on arXiv, in which he describes a method for constructing a graph of unit distances, which requires at least 5 colors to be painted.
Let's take a closer look at what kind of graph it is.
Count who built Jack
It all starts with a simple graph H consisting of 7 vertices and 12 edges:

Let's try to paint it in no more than 4 colors in various ways. It turns out that there are only 4 different ways to do this (up to turns, reflections and color order):

Note that in the upper two versions we have triples of monochrome vertices, which are located at the vertices of a regular triangle, and at the lower two, they are not. We call the coloring of the graph H bad if there is such a monochrome triple there, otherwise the coloring of H is good. Total, we have 2 bad coloring and 2 good.
Ok, go ahead. Consider a graph J, glued from 13 graphs H (find them all!):

Let's try to color graph J so that the colors of all the subgraphs of H included in it are good. A little patience, and we get 6 different variations (again, up to any equivalent transformations mentioned above; plus the colors of the vertices marked in black):

Black peaks can be painted in several ways, but painting them is not particularly important to us. Nevertheless, it is undesirable to throw them out of the J column - then “extra” painting options appear. Which, moreover, spoil all further constructions. Therefore, let the black peaks remain.
Now let's take a closer look at the resulting options. Namely, on the central vertex and on the 6 vertices, which are at a distance of 2 from the central one (a sort of graph H, doubled). We see that there are always used no more than two colors. Moreover, all options can be divided into 3 cases:
- a). All 7 vertices are of the same color.
- b). 4 vertices of 6 along the edges of the same color as the central one, and they go in a row by walking clockwise or counterclockwise. The remaining 2 vertices are of a different color.
- c). 2 vertices of 6 along the edges of the same color as the central one, and they are located diagonally relative to each other. The remaining 4 vertices are of a different color.
Let us remember these observations and move on to the graph K, which is composed of two copies of the graph J as follows: we superimpose one copy J on another so that the central vertices coincide, and then we twist them relative to each other so that each of the 6 vertices that we considered a little higher, one graph drove off from the corresponding vertex of another graph at a distance of exactly 1 (I noted these distances just below in blue). And here he is Count K:

Already getting a little difficult, isn't it?
Now let's again meditate a little on the resulting structure. Namely, let us understand what types of colorings for each copy of the graph J could be of the three that were listed above. Type a) there are no coloring pages, since whatever type the second copy is, we get two vertices of the same color at a distance of 1. Type b) are not there either: if the second copy is also type b), then some 2 vertices center colors "interfere" with each other; if the second copy has type c), then at least one vertex at the ends of the one-color diagonal will correspond to one of the four vertices of the first copy. Therefore, both copies of the graph J are painting type c)! And such paints are possible, because 4 vertices, which are painted in a color different from the central one, although they have the same color, in each of the copies this color may be different.
Now, since two copies of the graph J in the graph K contain type c), then the pairs of opposite vertices (out of 6 considered in each copy) have the same color. We take advantage of this observation and take another step. Namely, we construct the graph L from two copies of the graph K:

We superimpose the graphs K on each other as follows: we take in each of them a pair of opposite vertices and combine the first vertices in each pair (in the picture above it is marked with A), and the second ones are placed at a distance of exactly 1 (they are marked with B and C) . This technique is called overlapping of the graph (from the English. Spindling, where spindle is a spindle). For example, the Moser spindle is an overlap of a graph-rhombus composed of two triangles. Observing a little higher, the vertices A, B and C should be the same color, B and C at a distance of 1, so the graph L cannot be colored.
So what, we have proved everything? No, we just proved that the graph L cannot be painted in 4 colors so that the colors of all copies of the graph H (and there are already 52 of them!) Were good. Hence, in any painting of a graph L, painting of at least one graph H will be bad !
Bad paint graph H
This part, unfortunately, cannot be sorted out without the help of a computer. Therefore, we briefly analyze the further part of the constructions, for details you can refer to the original article, or by clicking on the links to Polymath below. The pictures taken from the original article are not of very high quality, but they make it possible to approximately understand what is happening.
So, first we build the graph V on 31 vertices, which consists of 5 graphs H, which are aligned with the centers and rotated to cunning angles relative to each other:

Next, we build the graph W as follows: make 31 copies of the graph V and place the center of each copy at each vertex of another graph V (this operation is called the Minkowski sum of two unit distance graphs, that is, we do ), after which we delete all vertices that are more than a distance from the center . So now we have a graph W for 301 vertices:

Now take the graph H and replace each of its vertices with a copy of the graph W (i.e., do ). As a result, we obtain the graph M at 1345 vertices:

The resulting graph M is essentially the union of a large heap of Moser's spindles in various positions. And, if we paint three vertices in one color at a pairwise distance of the original graph H, which we fluffed up to M, thus making the painting H bad, then the rest of the graph M cannot be painted in 4 colors. This fact is verified by computer search.
And finally, the last step: we now take this tin M at 1345 vertices and copy over each of the 52 copies of the graph H in the graph L. As a result, we get a full tin at 20425 vertices, which is called the graph N. And this graph cannot be painted in 4 colors: when painting a frame L, painting at least one of the subgraphs H will turn out to be bad, and for this subgraph H the corresponding copy M will not be completed to make up to the end.
Q.E.D.
Reduced graph
The graph at 20,425 vertices is a fairly large graph. Is it possible to build a smaller example? Can! In the original article, de Gray reduced the example to 1581 vertices with various cutoffs.
After the publication of the article, the mathematical community organized the Polymath16 project (as it was, for example, with the problem of prime numbers of twins ) in order to collectively reduce the graph obtained by de Gray to generalize the result to higher dimensions (for three-dimensional space, four-dimensional, and further), or even improve the lower limit of the chromatic number for the plane to 6.
By the way, in the same place they independently checked with the help of SAT-solvers that the example of de Gray on 1581 vertices can really be painted only in 5 colors, and also that its graph is a unit distance graph. So there is no doubt about the correctness of the result.
Graf de Gray is slowly decreasing. For example, the graph L by 121 vertices and 52 copies of the graph H can be slightly reduced to the graph L 'by 97 vertices and 40 copies of the graph H. The graph M with 1345 vertices has been reduced to the graph M' with only 278 vertices.
After replacing all the subgraphs H by M 'and the column L', the result can be improved further. At the time of this writing, the smallest unit distance graph found, which cannot be painted in 4 colors, has 610 vertices. Here is his picture (clickable):
Work continues. Maybe soon it will be possible to build a graph of unit distances, which can not be painted in 5 colors. And then - at 6, and then the problem of the chromatic number of the plane will be completely solved.
Source: https://habr.com/ru/post/358900/
All Articles
