Inverse kinematics in two-dimensional space
Part 1. Mathematics

Introduction
We are so accustomed to interacting with the world around us, that we do not think about how difficult our arms and legs move. In the academic literature, the task of controlling a robot arm is called inverse kinematics. Kinematics means " movement ", and the concept of " inverse " is due to the fact that we usually do not control the hand itself. We drive “engines” that turn every single part. Inverse kinematics is the task of determining how to move these engines in order to move the arm to a specific point. And in its general form, this task is extremely difficult. So that you understand how difficult it is, you can think of games such as QWOP , GIRP, or even Lunar Lander , in which you choose not where to move, but which muscles (or accelerators) to put into action.
The task of controlling movable drives extends even to the field of robotics. You should not be surprised that over the centuries maths and engineers have been able to develop many solutions. Most 3D editors and game engines (including Unity) have a set of tools that allow you to rivet humanoid and animal-like creatures. For various schemes (robot manipulators, tails, tentacles, wings, etc.), embedded solutions usually do not exist.
That is why in the previous series of articles on procedural animations and inverse kinematics, I proposed a very general and effective solution that can work with any scheme. But such power has a compromise: efficiency. One of the most important reasons for criticizing my article was that the method turned out to be too long and costly, while being used for hundreds of characters. Therefore, I decided to write a new article on the inverse kinematics of a manipulator in two degrees of freedom. The technique described in this tutorial is extremely effective and can be used for dozens (if not hundreds!) Of characters simultaneously.
Inverse kinematics
Let's imagine a robotic arm with two segments and two hinges, similar to the diagram below. At the end of the manipulator there is a final link that we want to control. We have no direct control over the position of the final link and can only rotate the hinges. The task of inverse kinematics is to find the best way to turn the connections to move the final link to the desired position.
')
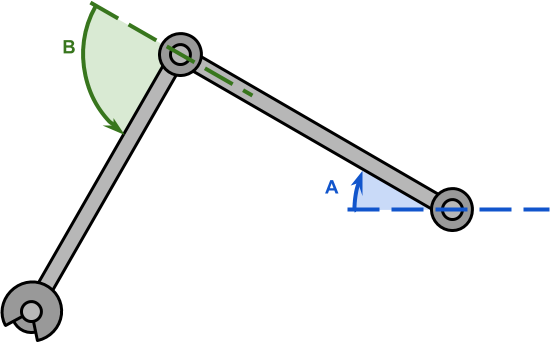
The solution proposed in this tutorial will work only for manipulators with two hinges. In academic literature it is often written that such manipulators have two degrees of freedom . And the reason for this is perfectly clear from the diagram below. The manipulator of a robot with two degrees of freedom can be modeled as a triangle, which is one of the most well-studied shapes in geometry.

Let's start by formalizing the task a bit. Two hinges A and B (both highlighted in black) can be rotated at corners A (blue) and B (green). This will cause the final link to move to position. C .
Inside corners
We can use three points. A , B and C to build a triangle with internal angles alpha , beta and gamma as in the example below.

Although all three corners are unknown to us, we know the length of all the edges.
- Section overlineAB denotes a hand and has a length c ;
- Section overlineBC denotes the forearm and has a length a ;
- Section overlineca denotes the distance between the hinge of the shoulder and the brush, and has a length b .
Knowledge of the three sides of the triangle is enough to find all three corners. This is possible thanks to the cosine theorem , which is a generalization of the Pythagorean theorem for triangles, which are not necessarily correct.
The two angles necessary to control the manipulator are alpha and beta . Let's start with alpha , which can be calculated using the cosine theorem:
$$ display $$ \ begin {equation *} a ^ 2 = b ^ 2 + c ^ 2 - 2 bc \ cos {\ alpha} \ end {equation *} $$ display $$
We can transform the equation to translate cos alpha :
\ begin {split} \ cos {\ alpha} & = \ frac {a ^ 2-b ^ 2-c ^ 2} {- 2bc} = \\ & = \ boxed {\ frac {b ^ 2 + c ^ 2-a ^ 2} {2bc}} \ end {split}
Now we need to apply the inverse cosine function cos−1 (also known as arccosine ) to find alpha :
$$ display $$ \ begin {equation *} \ alpha = \ cos ^ {- 1} {\ left (\ boxed {\ frac {b ^ 2 + c ^ 2-a ^ 2} {2bc}} \ right) } \ end {equation *} $$ display $$
Using the same procedure, we can again apply the cosine theorem to find beta :
b2=a2+c2−2ac cos beta
cos beta= fraca2+c2−b22ac
$$ display $$ \ begin {equation *} \ beta = \ cos ^ {- 1} {\ left (\ frac {a ^ 2 + c ^ 2 -b ^ 2} {2ac} \ right)} \ end { equation *} $$ display $$

Section h divides a triangle overset triangleABC into two right triangles: overset triangleABH and overset triangleBCH . This proof is a natural consequence of applying the Pythagorean theorem to both triangles:
$$ display $$ \ begin {equation *} \ begin {split} \ overset {\ triangle} {ABH}: & \\ & c ^ 2 = h ^ 2 + \ left (bd \ right) ^ 2 \\ & h ^ 2 = \ boxed {c ^ 2 - \ left (bd \ right) ^ 2} \ end {split} \ end {equation *} $$ display $$
$$ display $$ \ begin {equation *} \ begin {split} \ overset {\ triangle} {BCH}: & \\ & a ^ 2 = d ^ 2 + h ^ 2 \\ & h ^ 2 = \ boxed {a ^ 2 -d ^ 2} \ end {split} \ end {equation *} $$ display $$
Both equations are now relatively h2 . We can equate them both to get the following:
\ begin {split} \ boxed {a ^ 2 -d ^ 2} & = \ boxed {c ^ 2 - \ left (bd \ right) ^ 2} \\ a ^ 2 - d ^ 2 & = c ^ 2 - \ left (b ^ 2 + d ^ 2 - 2 bd \ right) \\ a ^ 2 - d ^ 2 & = c ^ 2 - b ^ 2 - d ^ 2 + 2 bd \ a ^ 2 \ xcancel { - d ^ 2} & = c ^ 2 - b ^ 2 \ xcancel {- d ^ 2} + 2 bd \\ a ^ 2 & = c ^ 2 - b ^ 2 + 2 bd \\ \ end {split}
what can be converted to:
$$ display $$ \ begin {equation *} c ^ 2 = a ^ 2 + b ^ 2-2bd \ end {equation *} $$ display $$
In this form, the cosine theorem is presented in the Euclidean Principles.
To get the modern look of the equation, we need to apply trigonometry. Since (5) is a regular triangle, we can express the segment d as:
$$ display $$ \ begin {equation *} d = a \ sin {\ delta} \ end {equation *} $$ display $$
Where delta can be found by remembering that the sum of the angles of a triangle is 180 circ (or, similarly, pi radians):
delta+ gamma+ frac pi2= pi delta= pi− frac pi2− gamma delta= frac pi2− gamma
Substituting delta , we get:
$$ display $$ \ begin {equation *} \ begin {split} d & = a \ sin {\ delta} \\ d & = a \ boxed {\ sin {\ left (\ frac {\ pi} {2} - \ gamma \ right)}} \\ d & = a \ boxed {\ cos {\ gamma}} \ end {split} \ end {equation *} $$ display $$
The final step is a well-known property:
sin left( frac pi2− gamma right)= cos gamma
Now we can substitute this, which gives us a modern view of the cosine theorem :
$$ display $$ \ begin {equation *} \ begin {split} c ^ 2 & = a ^ 2 + b ^ 2-2b \ boxed {d} \\ c ^ 2 & = a ^ 2 + b ^ 2-2b \ boxed {a \ cos {\ gamma}} \\ c ^ 2 & = a ^ 2 + b ^ 2-2ab \ cos {\ gamma} \ end {split} \ end {equation *} $$ display $$
Hinge angles
Using the cosine theorem, we calculated the values alpha and beta which are the inner corners of the triangle formed by the manipulator. However, we actually need angles A (blue) and B (green).

Let's start by calculating B that will be easier. From the picture shown above it is obvious that beta and B total give 180 circ (which is equal to pi radians). It means that:
$$ display $$ \ begin {equation *} \ begin {split} \ beta + B = \ pi \\ B = \ pi - \ beta \ end {split} \ end {equation *} $$ display $$
Calculation A not much different. The only difference here is that we need to consider A′ (purple) which is the cut angle overlineac . It can be calculated using the arc cotangent function tan−1 :
$$ display $$ \ begin {equation *} A '= \ tan ^ {- 1} {\ left (\ frac {C_Y-A_Y} {C_X-A_X} \ right)} \ end {equation *} $$ display $$
What gives us:
$$ display $$ \ begin {equation *} A = \ alpha + A '\ end {equation *} $$ display $$
Sign of angles A , A′ and B basically arbitrary and depends on the method of movement of each hinge.
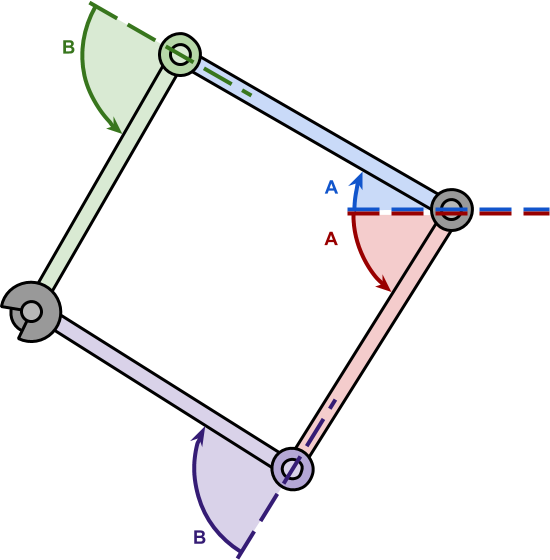
Although the corners A and B actually different, the output essentially remains the same, with a few exceptions.
Part 2. Code

Introduction
In the previous part, we considered the problem of inverse kinematics for a robot manipulator with two degrees of freedom.
In this case, the length of the manipulators is usually known. cc and a . If the point we want to reach is C , the configuration becomes a triangle, all sides of which are known.

Then we derived equations for the angles A and B controlling the pivot of the manipulator hinges:
$$ display $$ \ begin {equation *} A = \ underset {\ alpha} {\ underbrace {\ cos ^ {- 1} {\ left (\ frac {b ^ 2 + c ^ 2-a ^ 2} { 2bc} \ right)}}} + \ underset {A '} {\ underbrace {\ tan ^ {- 1} {\ left (\ frac {C_Y-A_Y} {C_X-A_X} \ right)}}} \ end {equation *} $$ display $$
$$ display $$ \ begin {equation *} B = \ pi - \ underset {\ beta} {\ underbrace {\ cos ^ {- 1} {\ left (\ frac {a ^ 2 + c ^ 2 -b ^ 2} {2ac} \ right)}}} \ end {equation *} $$ display $$
At first glance, they can look pretty frightening; on the other hand, their geometric interpretation is quite intuitive from the figure shown above.
Creating a robot manipulator
The first step in implementing this solution is to create a robot arm. The concept of "hinges" is unknown to the Unity engine. However, the parent element system in the engine can be used to create a hierarchy of components that will behave exactly like a robot manipulator.
The idea is to use a
GameObject for each hinge so that the rotation of its transform makes it rotate and a manipulator attached to it. Having made the second hinge a child of the first hinge, we will make them turn as in the first drawing.As a result, we get the following hierarchy:
- Root
- Hinge A
- Bone A
- Hinge B
- Bone B
- Arm
- Hinge A
Then we can add a script with the name
SimpleIK to the root object, which will perform hinge turns to reach the desired point. using System.Collections; using UnityEngine; namespace AlanZucconi.IK { public class SimpleIK : MonoBehaviour { [Header("Joints")] public Transform Joint0; public Transform Joint1; public Transform Hand; [Header("Target")] public Transform Target; ... } } The equations derived in the previous part of the tutorial require knowledge of the length of the first two bones (called respectively c and a ). Since the length of the bones should not change, they can be calculated in the
Start function. However, this requires the paddle to be in a good configuration when you start the game. private length0; private length1; void Start () { length0 = Vector2.Distance(Joint0.position, Joint1.position); length1 = Vector2.Distance(Joint1.position, Hand.position ); } Hinge Turns
Before showing the finished version of the code, let's start with a simplified. If we transfer equations (1) and (2) directly into the code, then as a result we get something like this:
void Update () { // Joint0 Target float length2 = Vector2.Distance(Joint0.position, Target.position); // float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0); float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg; // float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0); float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg; // Joint0 Target Vector2 diff = Target.position - Joint0.position; float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg; // Unity float jointAngle0 = atan - angle0; // A float jointAngle1 = 180f - angle1; // B ... } Mathematical functions cos−1 and tan−1 called in Unity
Mathf.Acos and Mathf.Atan2 . In addition, the final angles are converted to degrees using Mathf.Rad2Deg , because the Transform component should receive angles, not radians.Target unreachable goals
Although the code shown above seems to work, there is a condition under which it fails. What happens if the goal is unattainable? This is not taken into account in the current implementation, which leads to undesirable behaviors.
A common solution would be to completely stretch the arm towards the target. This behavior is consistent with the pullout movement that we seek to pretend.
The code shown below recognizes unattainable targets by checking whether the distance from the root to it is greater than the total length of the manipulator.
void Update () { float jointAngle0; float jointAngle1; float length2 = Vector2.Distance(Joint0.position, Target.position); // Joint0 Target Vector2 diff = Target.position - Joint0.position; float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg; // ? // , if (length0 + length1 < length2) { jointAngle0 = atan; jointAngle1 = 0f; } else { float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0); float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg; float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0); float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg; // Unity jointAngle0 = atan - angle0; jointAngle1 = 180f - angle1; } ... } Hinge Turns
Now we have to learn how to turn the hinges. This is done by accessing the
localEulerAngles property of the Transform hinge component. Unfortunately, we cannot change the angle z directly, so the vector needs to be copied, modified, and pasted. Vector3 Euler0 = Joint0.transform.localEulerAngles; Euler0.z = jointAngle0; Joint0.transform.localEulerAngles = Euler0; Vector3 Euler1 = Joint1.transform.localEulerAngles; Euler1.z = jointAngle1; Joint1.transform.localEulerAngles = Euler1; At this tutorial on inverse kinematics for two-dimensional manipulators is completed.
Source: https://habr.com/ru/post/358798/
All Articles