Part 1. Introducing the Marching cubes

How to create a mesh from any chaos
In Minecraft, we can dig in any direction, removing one block at a time with clearly defined edges. But in other games, developers manage to destroy the relief smoothly, without the cubicity of Minecraft.

Here is an example from No Man's Sky : video .

A similar technique is used to display images from MRI , metaballs, and voxelization of the relief.
')
In this part I will talk about the technique of creating the crumbling relief of the Marching Cubes, and in a more general application - to create a smooth boundary mesh of a solid object. In this article we will start with a two-dimensional technique, then a three-dimensional, and in the third part we will consider Dual Contouring. Dual Contouring is a more advanced technique that creates the same effect.

Our goal

To begin with, we will decide on what we want to achieve. Suppose we have a function that can be discretized over the whole space, and we want to plot its boundary on the graph. In other words, determine where the function performs the transition from positive to negative and vice versa. In the example with a destructible relief, we will interpret the positive areas as solid and the negative areas as empty.

A function is a great way to describe an arbitrary shape. but it does not help us draw it.

To draw, we need to know its boundary , for example, the points between positive and negative values, where the function intersects zero. The Marching Cubes algorithm takes such a function and creates a polygonal approximation of its boundary, which can be used for rendering. In 2d, this boundary will be a continuous line. When you go to 3d, it becomes a mesh.

Implementation of two-dimensional marching cubes

Note: this tutorial focuses more on concepts and ideas than on implementation methods and code. If you are more interested in the implementation, then examine the code in python , which contains the commented code with all necessary.

For simplicity, let's start with 2d, and later move on to 3d. I will call algorithms in 2d and in 3d “Marching Cubes”, because in essence they are one algorithm.

Step 1

First, we divide the space into a uniform grid of squares (cells). Then, for each cell, we can use the function calculation to determine whether each vertex of the cell is inside or outside a solid region.

Below is a function describing a circle, and black dots mark all vertices whose coordinates are positive.

Step 2

Then we process each cell separately, filling it with the appropriate boundary.


A simple lookup table provides 16 possible combinations of angles, either outside or inside. In each case, it determines which border should be drawn.


All combinations of two-dimensional marching cubes

Step 3

After repeating the process for all the cells, the boundaries are connected, creating a ready mesh, even though each cell was considered independently.


Fine! I think this is generally similar to the original circle described by the formula. But as you can see, it is all broken, and the segments are located at angles of 45 degrees. This happened because we decided to select the vertices of the borders (red squares) equidistant from the cell points.

Adaptability

The best way to get rid of angles of 45 degrees is an adaptive algorithm for marching cubes. Instead of simply specifying all the vertices of the borders from the central points of the cells, they can be positioned so that they best fit the solid region. For this we need not only to know whether the point is inside or outside; we also need to know how deep it is .

This means that we need some function that gives us a measure of how deep the point is inside / outside. It does not have to be exact, because we only use it for approximations. In the case of our ideal circle, which has a radius of 2.5 units, we apply the following function .

$$

$$f (x, y) = 2.5 - \ sqrt {x ^ 2 + y ^ 2}$$

In which positive values ​​are inside, and negative values ​​are outside.

Then we can use numerical values. $$$f$ on either side of the face, to determine how far along the face you need to position the point .


If you put everything together, it will look like this:


Despite the fact that we have the same vertices and segments as before, a slight change in position makes the resulting shape much more like a circle.

Part 2. Three-dimensional Marching Cubes

So, in 2D, we divide the space into a grid, and then for each vertex of the cell, we calculate where this point is - inside or outside the solid region. In a 2d grid, each square has 4 corners, and for each of them there are two options, that is, each cell exists $$$2 \ times 2 \ times 2 \ times 2 = 2 ^ 4 = 16$ possible combinations of angle states.

Then we fill the cell with our own segment for each of the 16 cases, and all the segments of all the cells are naturally joined together. We use adaptability to best fit these segments to the target surface.

The good news is that in the three-dimensional case, everything works almost the same. We divide the space into a grid of cubes, consider them separately, draw some edges for each cube, and they are connected, creating the desired mesh border.

The bad news is that the cube has 8 angles, that is, there is $$$2 ^ {8} = 256$ possible cases under consideration. And some of these cases are much more complex than in 2D.

The very good news is that we absolutely do not need to understand this. You can simply copy the cases I have collected and go directly to the results section (“Putting It All Together”), without thinking about all the difficulties. And then start reading about dual contouring, if you need a more powerful technique.

All difficulties

Note: this tutorial focuses more on concepts and ideas than on implementation methods and code. If you are more interested in the implementation, then study the implementation in 3D on python , which contains commented code with all necessary.

Are you still reading? Great, I like that.

The secret is that we are not really obligated to collect all 256 different cases. Many of them are mirror reflections or turns of each other.


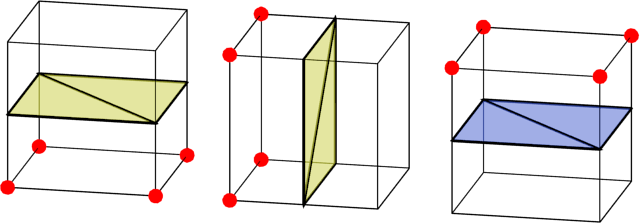
Here are three different cases of cells. The red corners are solid, all others are empty. In the first case, the bottom corners are solid, and the top corners are empty, therefore, to correctly draw the dividing border, it is necessary to divide the cell vertically. For convenience, I painted the outer side of the border yellow, and the inside - blue.

The remaining two cases can be found by simply turning the first case.

We can use another trick:


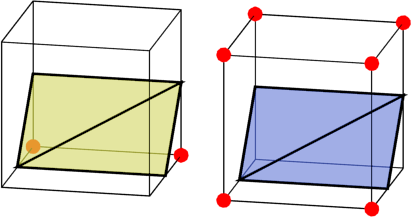
These two cases are opposite to each other - the solid corners of one are empty of the other, and vice versa. We can easily generate one case from another - they have the same border, only inverted.

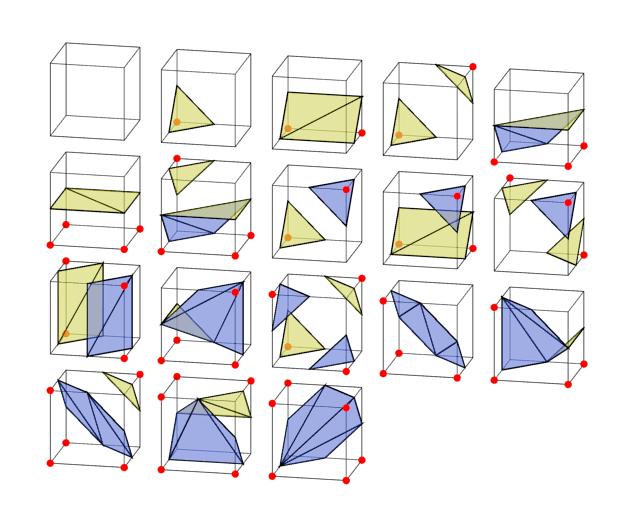
Given all this, in fact, we need to consider only 18 cases from which we can generate all the rest.

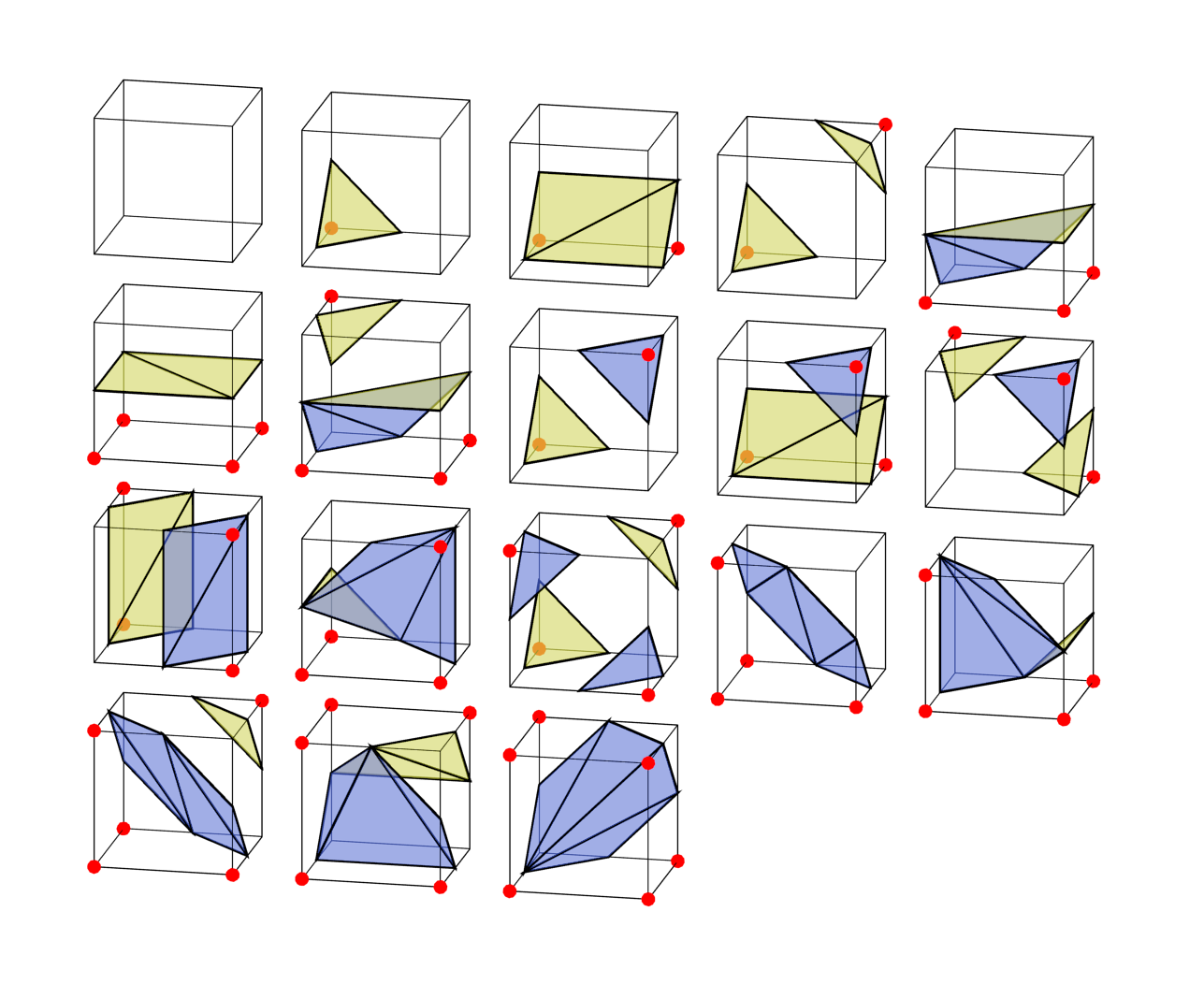
The only reasonable person

If you read the article on Wikipedia or most of the tutorials on the Marching Cubes, then they say that only 15 cases are needed. How so? Well, actually this is true - the three lower cases from my scheme are not necessarily necessary. Here again these three cases in comparison with other cases opposite to them, giving a similar surface.


Both the second and third columns correctly separate solid angles from empty ones. But only when we consider one cube separately. If you look at the edges of each face of a cell, you can see that they are different for the second and third columns. Inverted will not properly connect with adjacent cells, leaving holes in the surface. After adding three extra cases, all the cells are correctly connected.

We put everything together

As in the two-dimensional case, we can simply process all cells independently. Here is a spherical mesh created from the Marching Cubes.


As you can see, the shape of the sphere as a whole is done correctly, but in some parts there is a chaos of narrow generated triangles. You can solve this problem with the Dual Contouring algorithm, which is more advanced than the Marching Cubes.

Part 3. Dual Contouring

Marching Cubes are easy to implement, so they are often used. But the algorithm has many problems:

1. Complexity. Even though we only need to process one cube at a time, the Marching Cubes, as a result, turn out to be quite difficult, because it is necessary to consider many different cases.
   
   
   
2. Uncertainty. Some cases in Marching Cubes cannot be resolved in an obvious way in one way or another. If in 2d we have two opposite corners, then it is impossible to say whether they should connect or not.
   
   
   
   
   In 3d, the problem is further aggravated, because an uncoordinated sequence of elections can create a leaky mesh. In the second part, we had to write additional code to solve this problem.
3. Marching Cubes cannot create sharp edges and corners. Here is a square, approximated by the Marching Cubes.
   
   
   
   
   The corners were cut off. Adaptability cannot help here - Marching Squares always create straight line segments within any cell where the angle of the target square is.

What do we do?

Dual Contouring appears on stage

Note: this tutorial focuses more on concepts and ideas than on implementation methods and code. If you are more interested in the implementation, then examine the implementation in python, which contains the commented code with all necessary ( 2d and 3d ).

Dual Contouring solves these problems and is much more expandable. Its disadvantage is that we need even more information about $$$f (x)$ , that is, a function that determines what is solid and empty. We need to know not only the value $$$f (x)$ but also gradient $$$f '(x)$ . This additional information will improve adaptability compared to marching cubes.

Dual Contouring places one vertex into each cell, and then “connects the dots”, creating a full mesh. The points are joined along each edge that has a change of sign, as in the marching cubes.


Note: the word "dual" ("dual") in the name appeared because the cells in the grid become the vertices of the mesh, which connects us with the dual graph .

Unlike the Marching Cubes, we cannot calculate cells individually. In order to “connect the dots” and find the full mesh, we must consider the neighboring cells. But in fact, it is a much simpler algorithm than Marching Cubes, because there are no many individual cases. We simply find each edge with a change of sign and connect the vertices of the cells adjacent to this edge.

Getting gradient

In our simple example with a 2d circle of radius 2.5 $$$f$ is set as follows:

$$

$$f (x, y) = 2.5 - \ sqrt {x ^ 2 + y ^ 2}$$

(in other words, 2.5 minus the distance from the center point)

Using the differential calculus, we can calculate the gradient:

$$

$$f '(x, y) = \ text {Vec2} \ left (\ frac {-x} {\ sqrt {x ^ 2 + y ^ 2}}, \ frac {-y} {\ sqrt {x ^ 2 + y ^ 2}} \ right)$$

A gradient is a pair of numbers for each point, indicating how much the function changes as it moves along the x or y axis.

But to obtain the gradient function, we do not need complex calculations. We can just measure change $$$f$ when $$$x$ and $$$y$ deviate by a small amount $$$d$ .

$$

$$f '(x, y) \ approx \ text {Vec2} \ left (\ frac {f (x + d, y) - f (xd, y)} {2d}, \ frac {f (x, y + d) - f (x, yd)} {2d} \ right)$$

It will work for any smooth $$$f$ if selected $$$d$ quite a few. In practice, it turns out that even functions with sharp points turn out to be fairly smooth, because in order for this to work, it is not necessary to calculate the gradient near sharp sections. Link to code .

Adaptability

While we got the same stepped view, which was the Marching Cubes. We need to add adaptability. In the Marching Cubes algorithm, we chose where the vertex will be along the edge. Now we can freely choose any point of the internals of the cell.

We want to choose the point that most closely matches the information we received, i.e. calculated value

$$

$$f (x)$$

and gradient. Notice that we sampled the gradient along the edges, not in the corners.


Choosing the shown point, we guarantee that the displayed faces of this cell will correspond to the normals as much as possible:


In practice, not all the normals in the cell will fit. We need to choose the most suitable point. In the last section I will tell you how to choose this point.

Go to 3d

The cases in 2D and in 3d are not really very different. The cell is now a cube, not a square. We draw faces, not edges. But the differences end there. The procedure for selecting a single point in the cell looks the same. And we still find the edges with a change of sign, and then we connect the points of neighboring cells, but now four cells, which gives us a four-sided polygon:


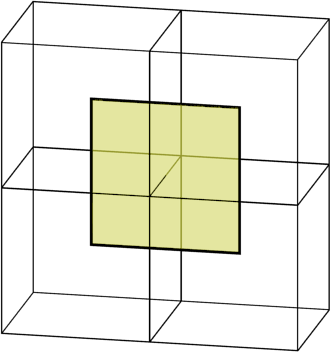
The face associated with a separate edge. She has points in each adjacent cell.

results

Dual contouring creates much more natural shapes than marching cubes, which can be seen in the sphere created with it:


In 3d, this procedure is reliable enough to select points located along the edge of a sharp section and the choice of angles when they occur.

Choosing a vertex location

A serious problem that I had previously ignored is the choice of the location of a point when the normals do not point to the same place.


In 3d, the problem is even more aggravated, because here there are more normals.

The solution is to select a point that is mutually best for all normals.

At first, for each normal, we assign a penalty for places remote from the ideal. Then we summarize all the penalty functions, which gives us a penalty in the form of an ellipse. After that we select the point with the smallest penalty.


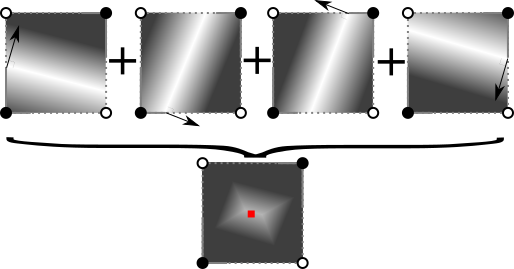
From a mathematical point of view, the individual penalty functions are the square of the distance from the ideal line for the current normal. The sum of all square members is a quadratic function , so the total penalty function is called a QEF (quadratic error function, quadratic error function). Finding the minimum point of a quadratic function is a standard procedure found in most matrix work libraries.

In my python implementation, I used the lstsq function from numpy.

Problems

Collinear normals

Most tutorials stop there, but the algorithm has a small dirty secret - the QEF solution in accordance with the description in the original article on Dual Contouring actually does not work very well.

Having solved the QEF, we can find the point that most closely matches the function normals. But in reality there are no guarantees that the resulting point is inside the cell .

In fact, quite often it is outside when we work with large flat surfaces. In this case, all the sampled normals will be the same or very close, as in this figure.


I have seen many tips for solving this problem. Some people gave up, discarding the gradient information and using instead the center of the cell or the average of the positions of the borders. This is called Surface Nets, and in this solution, at least, there is simplicity.

But based on my experience, I recommend using a combination of two techniques.

Technique 1: QEF Restricted Solution

Do not forget that we found the point of the cell, finding the point that minimizes the value of the given function, called QEF. By making small changes, we can find a minimizing point inside the cell.

Technique 2: QEF Offset

We can add any quadratic function to QEF and get another quadratic function that will be solved anyway. Therefore, I added a quadratic function that has a minimum point in the center of the cell.

Thanks to this, the entire QEF solution is pulled to the center.

In fact, this has a greater effect when the normals are collinear and most likely will give poor results, but have little effect on positions in a good case.

The use of both techniques is rather redundant, but it seems to me that it gives the best visual results.

More details on both techniques are shown in the code .

Self-crossing

Another dual contouring problem is that it can sometimes generate a self-intersecting 3d surface. In most cases, this is not paid attention, so I did not solve this problem.

There is an article that tells about her decision: "Intersection-free Contouring on An Octree Grid", Ju and Udeshi, 2006

Uniformity

Although the resulting dual contouring mesh is always sealed, the surface is not always well defined. Since the cell has only one point, when two surfaces pass through the cell, it will be common to them. This is called a “homogeneous” mesh and can cause problems with some texturing algorithms. The problem often arises when solid objects are thinner than the size of a cell or several objects almost touch each other.


The handling of such cases is a significant expansion of the functionality of the base Dual Contouring. If you need this function, I recommend to study this implementation of Dual Contouring or this article.

Algorithm extension

Due to the relative simplicity of creating Dual Contouring meshes, it is much easier to expand to work with cell diagrams that differ from the standard grids discussed above. As a rule, the algorithm can be performed for octree trees in order to obtain different cell sizes exactly where details are needed. In general, the idea is similar - we select by a point on a cell using sampled normals, then for each edge with a change of sign we find neighboring 4 cells and combine their vertices to the face. In octree, you can use recursion to find these edges and neighboring cells. Matt Keater has a detailed tutorial on this.

Another interesting extension is that for Dual Contouring we need only a definition of what is inside / outside and the corresponding normals. Although I said that we have a function to do this, we can extract the same information from another mesh. This allows us to perform a “strap”, i.e. generate a clean set of vertices and edges clearing the source mesh. An example is the Blender remesh modifier .

Additional reading

• Adjacent code
• Original article - Dual Contouring of Hermite Data - Tao Ju, Frank Losasso, Scott Schaefer, Joe Warren
• Dual Contouring is one of many similar techniques. See other approaches with their pros and cons in the SwiftCoder list .